Section 12 1 Probability Distributions Making a Probability

Section 12. 1 Probability Distributions

Making a Probability Distribution �Definition 1: A frequency table is a list of the outcomes in a sample space and the number of times each outcome occurs.

Example 1 �In the game Rock-Paper-Scissors, the scissors cut the paper, the rock dulls the scissors, and the paper covers the rock. Use the results below to make a frequency table for the winning players: Player 1, Player 2, or tie.

Probability �Definition 2: Probability over a continuous range of events is cumulative probability.

Example 2 �Social Science Use the frequency table. Find the probability that an elderly person living alone will have contact with his or her children more than once a week. �Find P(more than once a week) �Find P(once a week or more)

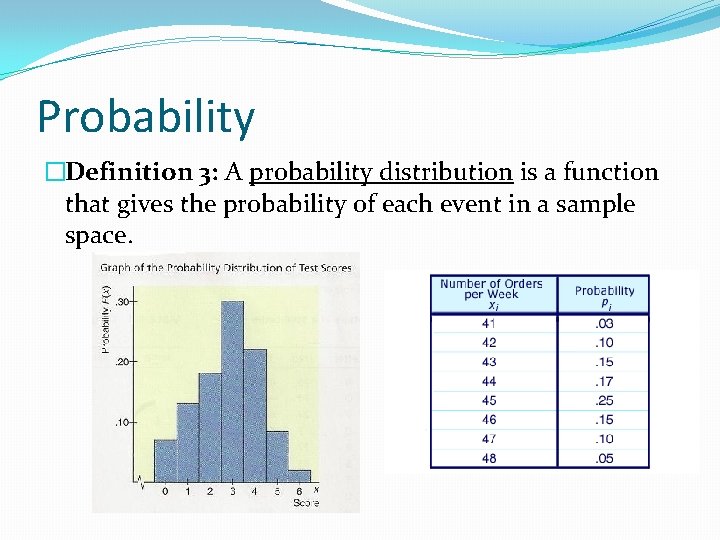
Probability �Definition 3: A probability distribution is a function that gives the probability of each event in a sample space.

Example 3 �Use a table and a graph to show the probability distribution for the spinner {red, green, blue, yellow}.

Example 4 �Genetics Use the information in the chart of inherited gene pairs. Graph the probability distribution for each sample space.

Example 4 Continued �a. Genotype Distribution b. Plant Color Distribution �c. Which probability distribution would be more useful to a farmer who wants to avoid raising white corn plants? Explain. �d. Make a probability distribution table for each sample space.

TOTD �Take a survey of your classmates’ eye colors and make a frequency table with the data.

Example 5 �Market Research At a certain store, the number of customers c who arrive at the checkout counter each minute varies according to the distribution below. Simulate the number of customers over a ten-minute period.

Example 5 Cont. �Step 1: Define how the simulation will be done. Use random numbers. Assign numbers from 1 to 100 to the events, based on the probability of each event. Use cumulative probabilities to help you assign the numbers.

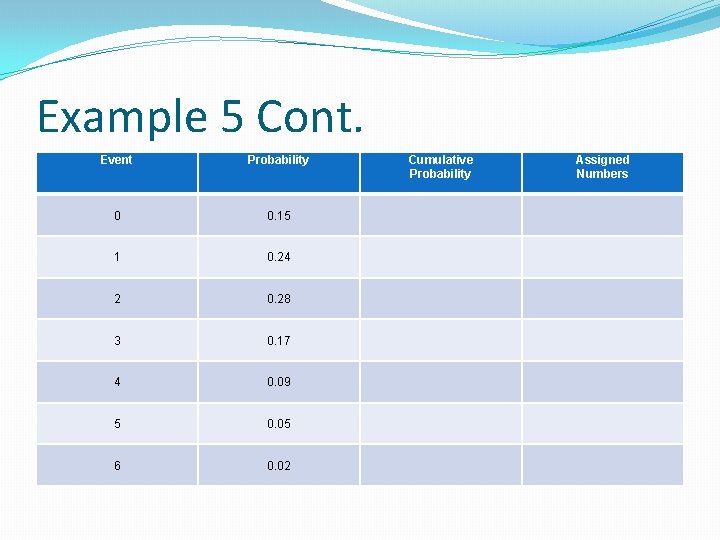
Example 5 Cont. Event Probability 0 0. 15 1 0. 24 2 0. 28 3 0. 17 4 0. 09 5 0. 05 6 0. 02 Cumulative Probability Assigned Numbers

Example 5 Cont. �Step 2: Conduct the simulation. Model a ten-minute period by generating ten random numbers from 1 – 100. �Step 3: Interpret the simulation. �Based on this simulation, a total of ___ customers would arrive at checkout counters over a ten-minute period.

TOTD �Use the frequency table. Find the probability that a student is involved in at least one extra-curricular activity.