Section 11 Lecture 2 Analysis of Supersonic Conical

Section 11 Lecture 2: Analysis of Supersonic Conical Flows • Anderson, Chapter 10 pp. 363 -375 MAE 5420 - Compressible Fluid Flow 1

Physical Aspects of Conical Flow • Flow is circumferentially symmetric • “Axi-symmetric flow” MAE 5420 - Compressible Fluid Flow 2

Physical Aspects of Conical Flow (cont’d) • Flow Properties are constant along a ray from the vertex MAE 5420 - Compressible Fluid Flow 3

Physical Aspects of Conical Flow (cont’d) • Look at shock wave “straight” • Shock strength is the same at points 1 and 2 “irrotational flow” MAE 5420 - Compressible Fluid Flow 4

Rotational and Irrotational Flow • Condition for Irrotational flow • At every point in flow field MAE 5420 - Compressible Fluid Flow 5

Spherical Coordinate System • Axi-symmetric flow is best represented using spherical coordinate system (Anderson conventions) MAE 5420 - Compressible Fluid Flow 6

Spherical Coordinate System (cont’d) • Velocity vector • Gradient vector • Divergence MAE 5420 - Compressible Fluid Flow 7

Continuity Equation for Conical Flow • Steady flow 0 • Axi-symmetric flow -- use spherical coordinates • Evaluating derivatives and letting MAE 5420 - Compressible Fluid Flow 8

Continuity Equation for Conical Flow (concluded) • Continuity Equation for Axi-symmetric Conical Flow MAE 5420 - Compressible Fluid Flow 9

Crocco’s Relation for Axi-symmetric Conical Flow • Irrotational flow • Crocco’s relationship solves both momentum and energy equation … thus for conical flow all we need to satisfy is: MAE 5420 - Compressible Fluid Flow 10

Crocco’s Relation for Axi-symmetric Conical Flow (cont’d) • For Arbitrary V • Curl Operation in Spherical Coordinates MAE 5420 - Compressible Fluid Flow 11

Crocco’s Relation for Axi-symmetric Conical Flow (cont’d) • For Arbitrary V • Curl Operation in Spherical Coordinates MAE 5420 - Compressible Fluid Flow 12

Crocco’s Relation for Axi-symmetric Conical Flow (cont’d) • Apply • Crocco Relation reduces to • Now apply MAE 5420 - Compressible Fluid Flow 13

Crocco’s Relation for Axi-symmetric Conical Flow (concluded) • Crocco Relation reduces to (wow!) • Irrotationality Condition for Axi-symmetric conical flow MAE 5420 - Compressible Fluid Flow 14

Euler’s Equation for Axi-symmetric Conical Flow • Steady Axi-symmetric conical flow 0 • Flow is irrotational … Apply along stream line direction MAE 5420 - Compressible Fluid Flow 15

Euler’s Equation for Axi-symmetric Conical Flow (cont’d) • Steady Axi-symmetric conical flow Divide by dr • Thus behind the shock wave MAE 5420 - Compressible Fluid Flow 16

Euler’s Equation for Axi-symmetric Conical Flow (cont’d) • But from enthalpy equation MAE 5420 - Compressible Fluid Flow 17

Euler’s Equation for Axi-symmetric Conical Flow (concluded) • Sub into Euler’s equation MAE 5420 - Compressible Fluid Flow 18

Collected Equations for Axi-symmetric Conical Flow • Only q is independent variable Can re-write partials at total derivatives MAE 5420 - Compressible Fluid Flow 19

Collected Equations for Axi-symmetric Conical Flow MAE 5420 - Compressible Fluid Flow (cont’d) 20

Collected Equations for Axi-symmetric Conical Flow (cont’d) • Substituting in MAE 5420 - Compressible Fluid Flow 21

Collected Equations for Axi-symmetric Conical Flow (cont’d) • CLASSICAL FORM OF TAYLOR-MACCOLL EQUATION … BUT DIFFICULT TO SOLVE NUMERICALLY IN THIS FORM MAE 5420 - Compressible Fluid Flow 22

Taylor-Maccoll Equation • O. D. E for Vr in terms of q Vr --> dependent variable, q --> independent variable MAE 5420 - Compressible Fluid Flow • Solve for Vr ---> Then 23

Taylor-Maccoll Equation (cont’d) • BETTER SOLUTION …Nondimensionalize by • let MAE 5420 - Compressible Fluid Flow • and the Taylor-Maccol equation reduces to 24

Taylor-Maccoll Equation (cont’d) MAE 5420 - Compressible Fluid Flow 25

Taylor-Maccoll Equation (cont’d) • Take a closer look at: • Once we find we can calculate M • So how do we find MAE 5420 - Compressible Fluid Flow ? 26

Numerical Procedure for Solving Axi-symmetric Conical Flow Field • Re-write • As • But • Substitute in MAE 5420 - Compressible Fluid Flow 27

Numerical Procedure for Solving Axi-symmetric Conical Flow Field • Re-write • As • But • Substitute in MAE 5420 - Compressible Fluid Flow 28

Numerical Procedure for Solving Axi-symmetric Conical Flow Field (cont’d) • Solve for MAE 5420 - Compressible Fluid Flow 29

Numerical Procedure for Solving Axi-symmetric Conical Flow Field (cont’d) • System of first order ordinary differential equations MAE 5420 - Compressible Fluid Flow 30

Numerical Procedure for Solving Axi-symmetric Conical Flow Field (cont’d) • Can be written in vector form as MAE 5420 - Compressible Fluid Flow 31

Numerical Procedure for Solving Axi-symmetric Conical Flow Field (cont’d) • Or MAE 5420 - Compressible Fluid Flow 32

Boundary Value Problem • Inverse solution method • Given M … Start with assumed bshock (initial condition) • Properties immediately behind Shock given by Oblique Shock relations • On cone Jq=0 Boundary Condition MAE 5420 - Compressible Fluid Flow 33

Boundary Value Problem (cont’d) • Starting Conditions Given M … Start with assumed bshock (initial condition) Calculate M 2 (immediately behind shock) MAE 5420 - Compressible Fluid Flow 34

Boundary Value Problem (cont’d) • Starting Conditions MAE 5420 - Compressible Fluid Flow 35

Boundary Value Problem (cont’d) • Using Starting Jr, Jq Integrate the equations of motion over increments of q Until Jq =0 … this angle corresponds t the solid Cone boundary corresponding to M and the assumed bshock. • So How do we integrate This? MAE 5420 - Compressible Fluid Flow 36

Integration of Equations of Motion • The Integral starts at bshock and proceeds towards the cone where q=qcone • Look at small segment dq for the integral MAE 5420 - Compressible Fluid Flow 37

Integration of Equations of Motion (cont’d) • Look at • Approximate are under curve = MAE 5420 - Compressible Fluid Flow 38

Integration of Equations of Motion (cont’d) • The the integral is approximated by • And “trapezoidal rule” MAE 5420 - Compressible Fluid Flow 39

Integration of Equations of Motion (cont’d) • Or we perform the same argument using “finite differences” • Basic differencing scheme MAE 5420 - Compressible Fluid Flow 40

Predictor / Corrector • But at step (j) we don’t know • So we predict it … • and then correct the prediction MAE 5420 - Compressible Fluid Flow • Be very careful About units on Dq 41

Predictor / Corrector • Where MAE 5420 - Compressible Fluid Flow 42

Collected Algorithm 1) Compute Initial Conditions, 1. a) Given M … Start with assumed bshock 2. b) Calculate M 2 (immediately behind shock) MAE 5420 - Compressible Fluid Flow 43

Collected Algorithm 1) Compute Initial Conditions, 1. c) Calculate p 2, T 2 ratios (immediately behind shock) MAE 5420 - Compressible Fluid Flow 44

Collected Algorithm (cont’d) 1) Compute Initial Conditions, 1. c) Compute starting non-dimensional velocities MAE 5420 - Compressible Fluid Flow 45

Collected Algorithm (cont’d) 2) Compute q decrement 3) Integration Loop, j=1, …N 1. • Be very careful About units on Dq a) Predictor ; 2. b) Corrector MAE 5420 - Compressible Fluid Flow 46

Collected Algorithm (cont’d) 3) Integration Loop, j=1, …N (cont’d) 1. d) Test for convergence 2. if Jq > 0 you have a problem Why? MAE 5420 - Compressible Fluid Flow 47

Collected Algorithm (cont’d) 4) Post-process data a) Compute total J b) Compute Mcone • Why? MAE 5420 - Compressible Fluid Flow 48

Collected Algorithm (cont’d) 4) Post-process data c) Calculate pcone, Tcone ratios (flow behind shock is isentropic) MAE 5420 - Compressible Fluid Flow 49

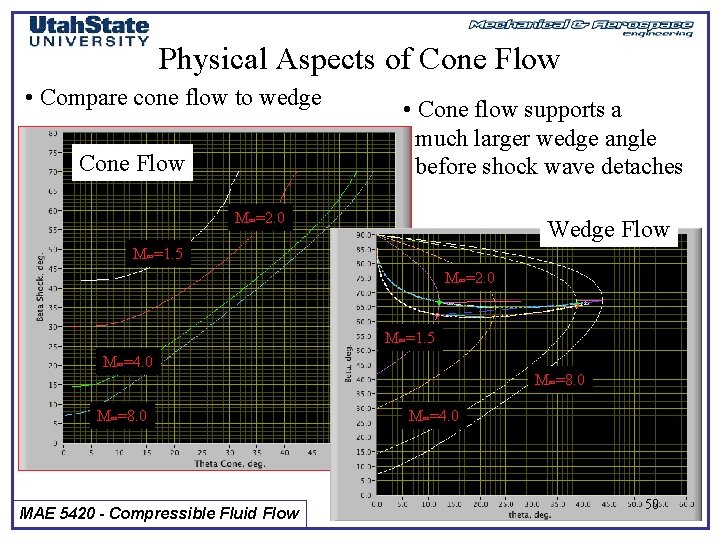
Physical Aspects of Cone Flow • Compare cone flow to wedge Cone Flow • Cone flow supports a much larger wedge angle before shock wave detaches M =2. 0 Wedge Flow M =1. 5 M =2. 0 M =1. 5 M =4. 0 M =8. 0 MAE 5420 - Compressible Fluid Flow M =4. 0 50

Physical Aspects of Cone Flow (cont’d) • Three-dimensional “relieving” effect • Cone shock wave is Effectively weaker Than shock wave for Corresponding wedge angle MAE 5420 - Compressible Fluid Flow 51

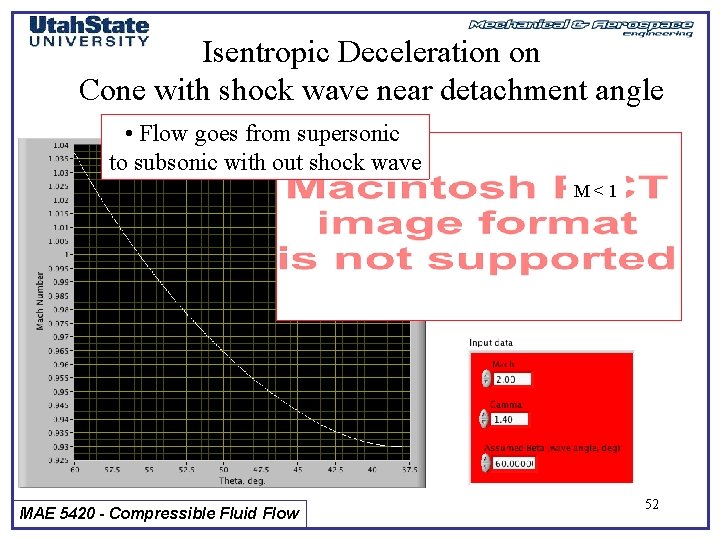
Isentropic Deceleration on Cone with shock wave near detachment angle • Flow goes from supersonic to subsonic with out shock wave M<1 MAE 5420 - Compressible Fluid Flow 52

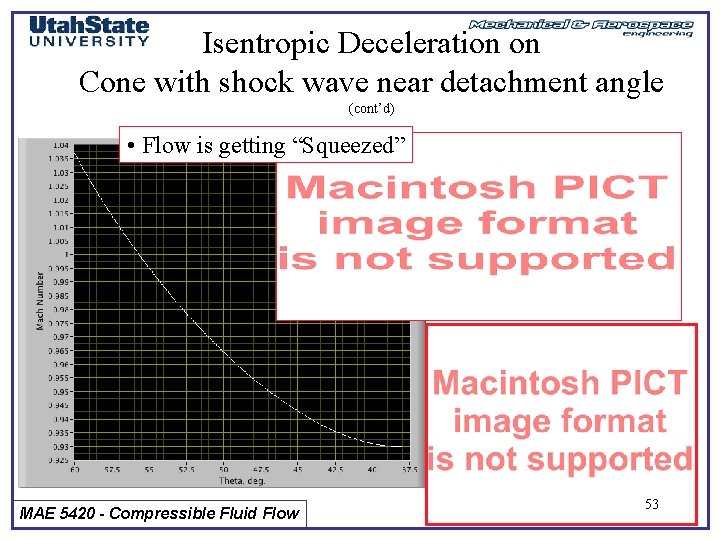
Isentropic Deceleration on Cone with shock wave near detachment angle (cont’d) • Flow is getting “Squeezed” MAE 5420 - Compressible Fluid Flow 53

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack • Look at Zero-a conical flow field projected onto spherical surface • Really a special case Of a 1 -dimensional Flow field • Shock strength is uniform … irrotational flow field Crocco’s Theorem MAE 5420 - Compressible Fluid Flow • Simplifying conditions result in flow field That is “easy” to solve 54

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • Look at Non Zero-a conical flow field • Shock Strength is no longer uniformly strong • Tds is no longer constant • Flow field is “rotational” MAE 5420 - Compressible Fluid Flow 55

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • Look at Non Zero-a conical flow field 1) 2) 3) Flow field is a function of two independent variables q, 1. 2. �hock wave angle bs is different for each meridional plane ( ) 3) Stream lines about body are curved 4) From windward to leeward surface 5) 6) 7) Stream lines that pass thru different Point on shock wave experience different Entropy changes MAE 5420 - Compressible Fluid Flow 56

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • “Vortical Singularity” • Stream lines with different entropy levels converge on a single line on leeward side • Ray along cone surface at 180∞ degrees to freestream wind has “multi-valued” entropy level • Referred to as “Vortical Singularity” MAE 5420 - Compressible Fluid Flow 57

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • When a < qcone … singularity lies along cone surface MAE 5420 - Compressible Fluid Flow 58

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • When a > qcone … singularity lies above cone surface MAE 5420 - Compressible Fluid Flow 59

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • Cross Flow Sonic Lines, cross flow Mach number > 1 MAE 5420 - Compressible Fluid Flow 60

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • Cross Flow Sonic Lines, cross flow Mach number > 1 MAE 5420 - Compressible Fluid Flow 61

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • “Small angle” approximation • Solution formulated as “corrections” to zero-a solution Zero alpha condition “Correction” MAE 5420 - Compressible Fluid Flow 62

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • “Taylor-Maccoll” type of equation for alpha perturbations • Boundary conditions (behind shock wave) MAE 5420 - Compressible Fluid Flow 63

Qualitative Aspects of Conical Supersonic Flow Fields at Angles of Attack (cont’d) • Solution is similar (but more complex) than zero alpha case Starts at shock wave and works toward surface • Solution tables for right cones NASA SP 3007 "Tables for Flow Around Right Circular Cones at Small Angle of Attack" Link to paper in appendix to this section MAE 5420 - Compressible Fluid Flow 64

Homework 12 • Code Taylor-Maccoll algorithm for cone flow • Solve for flow conditions on surface of Cone at freestream Mach 2. 0 with 15 half angle p T r = = = 101. 325 k. Pa 288 � 1. 23 kg/m 3 15 MAE 5420 - Compressible Fluid Flow 65

Part 1 Solution 11. 1 MAE 5420 - Compressible Fluid Flow 66

Homework 12 (Continued) • Define • Hint: You’ll have to do trial And error for each mach number to get the Shock angle correct • Derive an expression for the cone wave drag as a function of the cone surface pressure (pcone) and the base pressure (pbase) • Assume pbase = p plot CDcone versus Mach over range from 1. 5 to 7 MAE 5420 - Compressible Fluid Flow 67

11. 2 Part 2 Solution MAE 5420 - Compressible Fluid Flow 68

Part 2 Solution MAE 5420 - Compressible Fluid Flow (cont’d) 69

Part 2 Solution (concluded) Cone Drag Coefficient versus Mach Number MAE 5420 - Compressible Fluid Flow 70