Section 10 7 Objective 1 Gain an understanding

Section 10. 7 Objective 1. Gain an understanding of some of the general ideas of other kinds of geometries. 1/8/2022 Section 10. 7 1

The Geometry of Graphs (Graph Theory) • The Swiss mathematician Leonhard Euler (1707 – 1783) proved that it was not possible to stroll through the city of Kőnigsberg, Germany by crossing each of 7 bridges exactly once. • His solution opened up a new kind of geometry called graph theory. 1/8/2022 Section 10. 7 2

Graph Definitions • Vertex is a point. • Edge is a line segment or curve that starts or ends at a vertex. • Graph consists of vertices and edges • Odd vertex has an odd number of attached edges. • Even vertex has an even number of attached edges. 1/8/2022 Section 10. 7 3

Rules of Traversability 1. A graph with all even vertices is traversable. One can start at any vertex and end where one began. 2. A graph with two odd vertices is traversable. One must start at either of the odd vertices and finish at the other. 3. A graph with more than two odd vertices is not traversable. A graph is traversable if it can be traced without lifting the pencil from the paper and without tracing an edge more than once. 1/8/2022 Section 10. 7 4

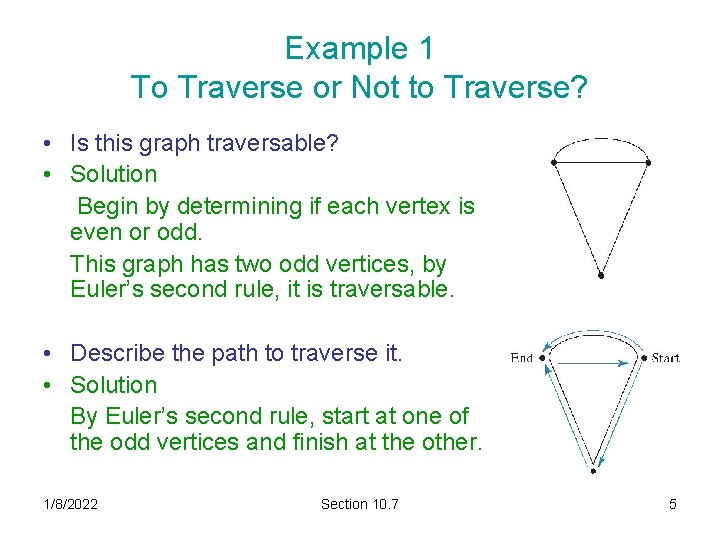
Example 1 To Traverse or Not to Traverse? • Is this graph traversable? • Solution Begin by determining if each vertex is even or odd. This graph has two odd vertices, by Euler’s second rule, it is traversable. • Describe the path to traverse it. • Solution By Euler’s second rule, start at one of the odd vertices and finish at the other. 1/8/2022 Section 10. 7 5

Topology The Study of Shapes • Objects are classified according to the number of holes in them, called their genus. • Genus is the number of cuts that can be made in the object without cutting the object in two pieces. • Topologically Equivalent objects have the same genus. • The topology of knots is used to identify viruses and how they invade our cells. 1/8/2022 Section 10. 7 6

Examples of Topologically Equivalency • The three shapes below have the same genus: 0. No complete cuts can be made without cutting these objects into two pieces. • A doughnut and a coffee cup have a genus of 1. 1/8/2022 Section 10. 7 7

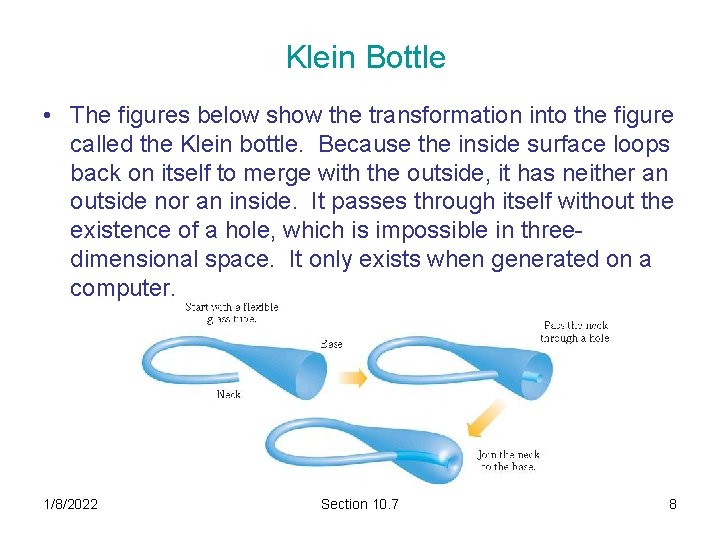
Klein Bottle • The figures below show the transformation into the figure called the Klein bottle. Because the inside surface loops back on itself to merge with the outside, it has neither an outside nor an inside. It passes through itself without the existence of a hole, which is impossible in threedimensional space. It only exists when generated on a computer. 1/8/2022 Section 10. 7 8

Comparing the Three Systems of Geometry (Euclidean and non-Euclidean) Euclidean Geometry Euclid (300 B. C. ) Hyperbolic Geometry Lobachevsky, Bloyai (1830) Given a point not on a line, there is one and only one line through the point parallel to the given line. Given a point not on a line, there There are no parallel are an infinite number of lines through the point that do not intersect the given line. Geometry is on a plane: Geometry is on a pseudosphere: Geometry is on a sphere: 1/8/2022 Section 10. 7 Elliptic Geometry Riemann(1850) 9

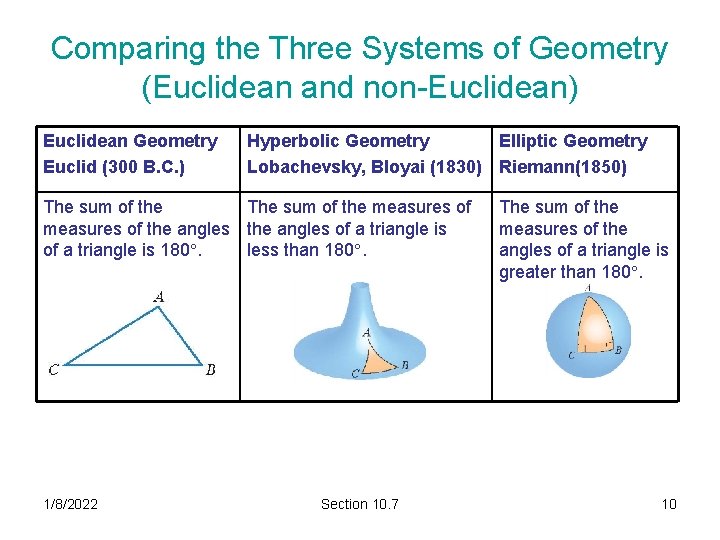
Comparing the Three Systems of Geometry (Euclidean and non-Euclidean) Euclidean Geometry Euclid (300 B. C. ) Hyperbolic Geometry Elliptic Geometry Lobachevsky, Bloyai (1830) Riemann(1850) The sum of the measures of the angles of a triangle is 180. less than 180. 1/8/2022 Section 10. 7 The sum of the measures of the angles of a triangle is greater than 180. 10

Fractal Geometry • Developed by Benoit Mandelbrot using computer programming. • Geometry of natural shapes. • Self-similarity is the quality of smaller versions of an object appearing in the object itself. • Iteration is the process of repeating a rule again and again to create a self-similar fractal. 1/8/2022 Section 10. 7 11