Section 10 4 Perimeters Areas of Similar Figures

Section 10– 4 Perimeters & Areas of Similar Figures Objectives: 1) To find perimeters & areas figures. of similar

Reminder of Perimeter & Area ► Perimeter – Distance around a figure § Perimeter of any polygon - add up the lengths of all of the sides § Perimeter of a circle – Circumference § C = 2 r ► Area – How much 2 D space it takes up § A// = bh § AΔ = ½ bh § A = r 2

Thm(8 – 6) Perimeters & Areas of similar figures ► If the similarity (side) ratio of 2 similar figures is a/b, then § The ratio of their perimeters is a/b. § The ratio of their areas is a 2/b 2. a b

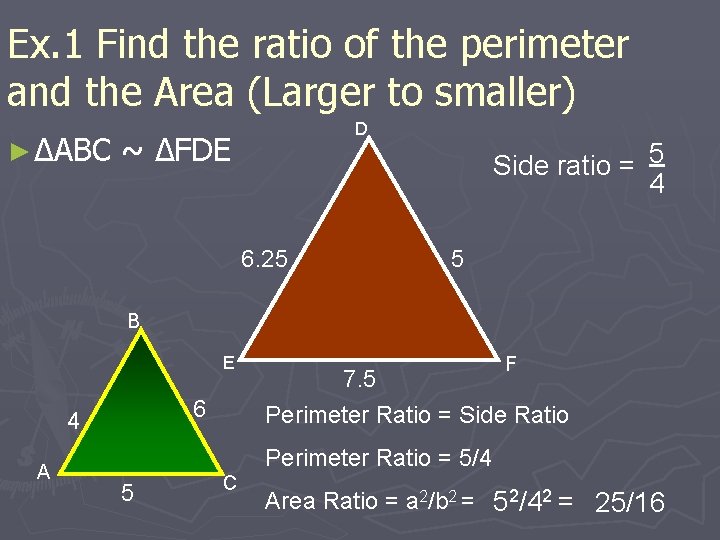
Ex. 1 Find the ratio of the perimeter and the Area (Larger to smaller) ► ΔABC D ~ ΔFDE 6. 25 Side ratio = 5 4 5 B E 6 4 A F 7. 5 Perimeter Ratio = Side Ratio Perimeter Ratio = 5/4 5 C Area Ratio = a 2/b 2 = 52/42 = 25/16

Ex. 2: Find the area ► The ratio of the lengths of the corresponding sides of 2 regular octagons is 8/3. The area of the larger octagon is 320 ft 2. Find the area of the smaller octagon. 8 Side ratio = 3 82 Area ratio = 32 = 64 9 Large side Small side 64 = 320 9 x Now, set up an area proportion using the area ratio! Large Area x = 45 ft 2

Ex. 3: Find the side ratio ► The areas of 2 similar pentagons are 32 in 2 and 72 in 2. What is their similarity (side) ratio? What is the ratio of their perimeter. Reduce 32 = 4 = 2 3 72 9 Remember: Side ratio is a/b and area ratio is a 2/b 2. So if the area ratio is given, you must take the square root of the numerator and the denominator. Area Ratio Side Ratio and the Perimeter ratio

Ex. 4: Find the perimeter & area of similar figures. ► The similarity (side) ratio of two similar Δ is 5: 3. The perimeter of the smaller Δ is 36 cm, and its area is 18 cm 2. Find the perimeter & area of the larger Δ. Write the side ratio and then find the perimeter. 5 = P 3 36 PL = 60 cm 52 = 32 Write the area ratio and then find the area. 25 = A 9 18 A = 50 cm 2

What have I Learned? ? ► Side Ratio = a/b ► Perimeter Ratio = a/b ► Area Ratio = a 2/b 2 ► If perimeters are given: § Write as a ratio § Reduce to simplest form for the side ratio ► If § § § Areas are given: Write as a ratio Reduce until 2 perfect squares are reached. Square Root (√) both numerator & denominator for the side ratio