Section 10 4 Finding Equations of Exponential Function
















- Slides: 18

Section 10. 4 Finding Equations of Exponential Function Copyright © 2011 Pearson Education, Inc.

Finding an Equation of an Exponential Curve Using the Base Multiplier Property to Find Exponential Functions Example An exponential curve contains the points listed in the table. Find an equation of the curve. Solution x • Exponential is of the form f(x) = ab • y-intercept is (0, 3), so a = 3 • Input increases by 1, output multiplies by 2: b = 2 x • f(x) = 3(2) Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 2

Finding an Equation of an Exponential Curve Using the Base Multiplier Property to Find Exponential Functions Solution Continued • Verify results using graphing calculator 2 nd Tblset 2 nd Table Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 3

Linear versus Exponential Functions Using the Base Multiplier Property to Find Exponential Functions Example 1. Find a possible equation of a function whose input – output pairs are listed in the table. Solution • x increases by 1, y multiplies by 1/3: b = 1/3 • y-intercept is (0, 162): a = 162 • Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 4

Linear versus Exponential Functions Using the Base Multiplier Property to Find Exponential Functions Example 2. Find a possible equation of a function whose input – output pairs are listed in the table. Solution • x increases by 1, y subtracted by 4: Linear function • y-intercept is (0, 50) • y = -4 x + 50 Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 5

Linear versus Exponential Functions Solving Equations of the Form abn = k for b Example Find all real-number solutions. Solution 1. • Solutions are 5 and – 5 • Use the notation 5 Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 6

Linear versus Exponential Functions Solving Equations of the Form abn = k for b Solution 2. 3. Check that both – 2 and 2 satisfy the equation. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 7

Linear versus Exponential Functions Solving Equations of the Form abn = k for b Solution 4. Check that 1. 55 approx. satisfies the equation. 6 5. The equation b = – 28 has no real solution, since an even exponent gives a positive number. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 8

n Solving Equations of the Form b = k for b Solving Equations of the Form abn = k for b Summary n To solve an equation of the form b = k for b, 1. If n is odd, the real-number solution is 2. If n is even, and k ≥ 0, the real-number solutions are. 3. If n is even and k < 0, there is no real number solution. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 9

One-Variable Equations Involving Exponents Solving Equations of the Form abn = k for b Example Find all real-number solutions. Round your answer to the second decimal place. 6 1. 5. 42 b – 3. 19 = 43. 74 2. Solution Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 10

One-Variable Equations Involving Exponents Solving Equations of the Form abn = k for b Solution Continued 2. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 11

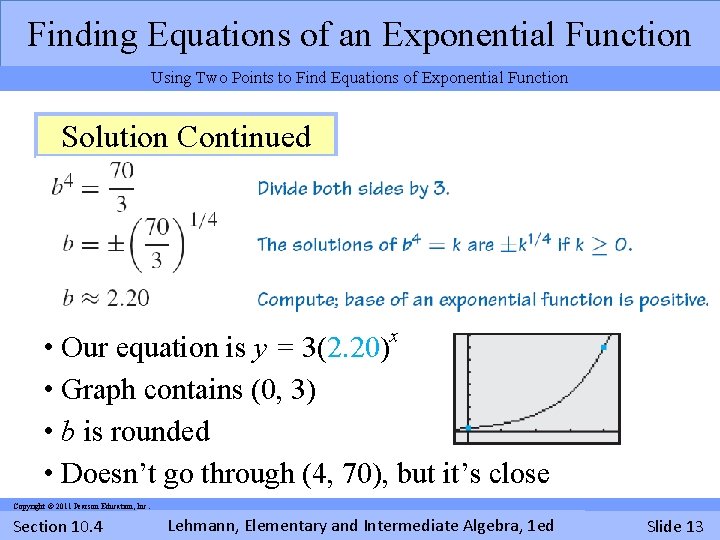
Finding Equations of an Exponential Function Using Two Points to Find Equations of Exponential Function Example x Find an approximate equation y = ab of the exponential curve that contains the points (0, 3) and (4, 70). Round the value of b to two decimal places. Solution x • y-intercept is (0, 3): y = 3 b • Substitute (4, 70) and solve for b Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 12

Finding Equations of an Exponential Function Using Two Points to Find Equations of Exponential Function Solution Continued x • Our equation is y = 3(2. 20) • Graph contains (0, 3) • b is rounded • Doesn’t go through (4, 70), but it’s close Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 13

Dividing Left Sides and Right Sides of Two Equations Using Two Points to Find Equations of Exponential Function Property If a = b and c = d, then In words: The quotient of the left sides of two equations is equal to the quotient of the right sides. Example x Find an approximate equation y = ab of the exponential curve that contains (2, 5) and (5, 63). Round the values of a and b to two decimal places. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 14

Finding an Equation of an Exponential Curve Using Two Points to Find Equations of Exponential Function Solution • Both points must satisfy the equation; so, • It’s easier to solve if we switch the equations • Divide left and right sides (a and b non zero) Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 15

Finding an Equation of an Exponential Curve Using Two Points to Find Equations of Exponential Function Solution Continued • Apply the property: • Solve for b by finding the cube root of 63/5 Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 16

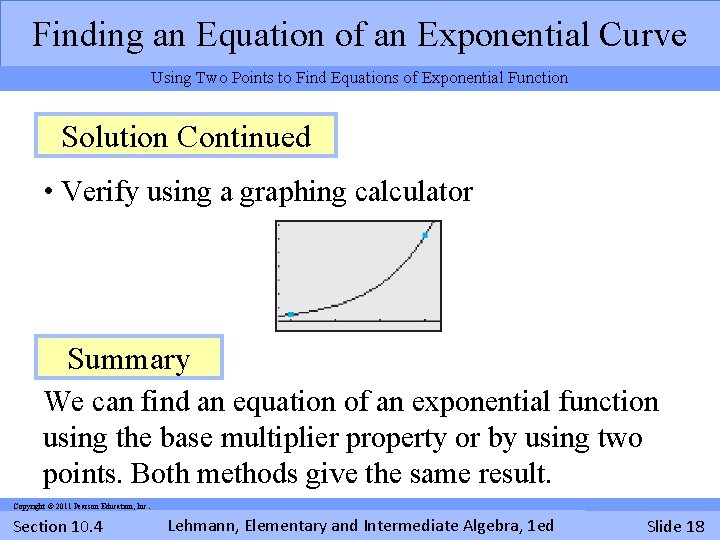
Finding an Equation of an Exponential Curve Using Two Points to Find Equations of Exponential Function Solution Continued • Substitute 2. 33 for b • Substitute (2, 5) and solve for a x • y = 0. 92(2. 33) approx. passes (2, 5) and (5, 63) Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 17

Finding an Equation of an Exponential Curve Using Two Points to Find Equations of Exponential Function Solution Continued • Verify using a graphing calculator Summary We can find an equation of an exponential function using the base multiplier property or by using two points. Both methods give the same result. Copyright © 2011 Pearson Education, Inc. Section 10. 4 Lehmann, Elementary and Intermediate Algebra, 1 ed Slide 18