Section 10 1 Exploring Quadratic Graphs Vocabulary Quadratic
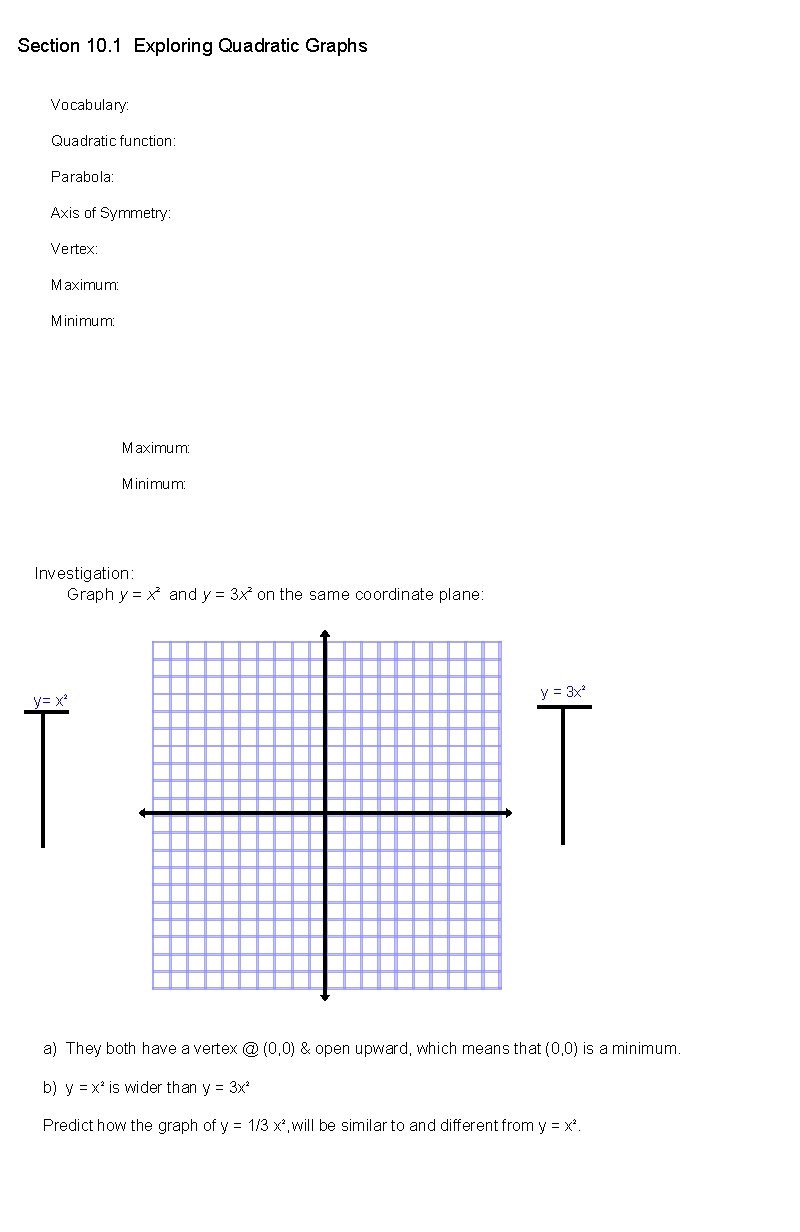
Section 10. 1 Exploring Quadratic Graphs Vocabulary: Quadratic function: Parabola: Axis of Symmetry: Vertex: Maximum: Minimum: Investigation: Graph y = x 2 and y = 3 x 2 on the same coordinate plane: y= x 2 y = 3 x 2 a) They both have a vertex @ (0, 0) & open upward, which means that (0, 0) is a minimum. b) y = x 2 is wider than y = 3 x 2 Predict how the graph of y = 1/3 x 2, will be similar to and different from y = x 2.
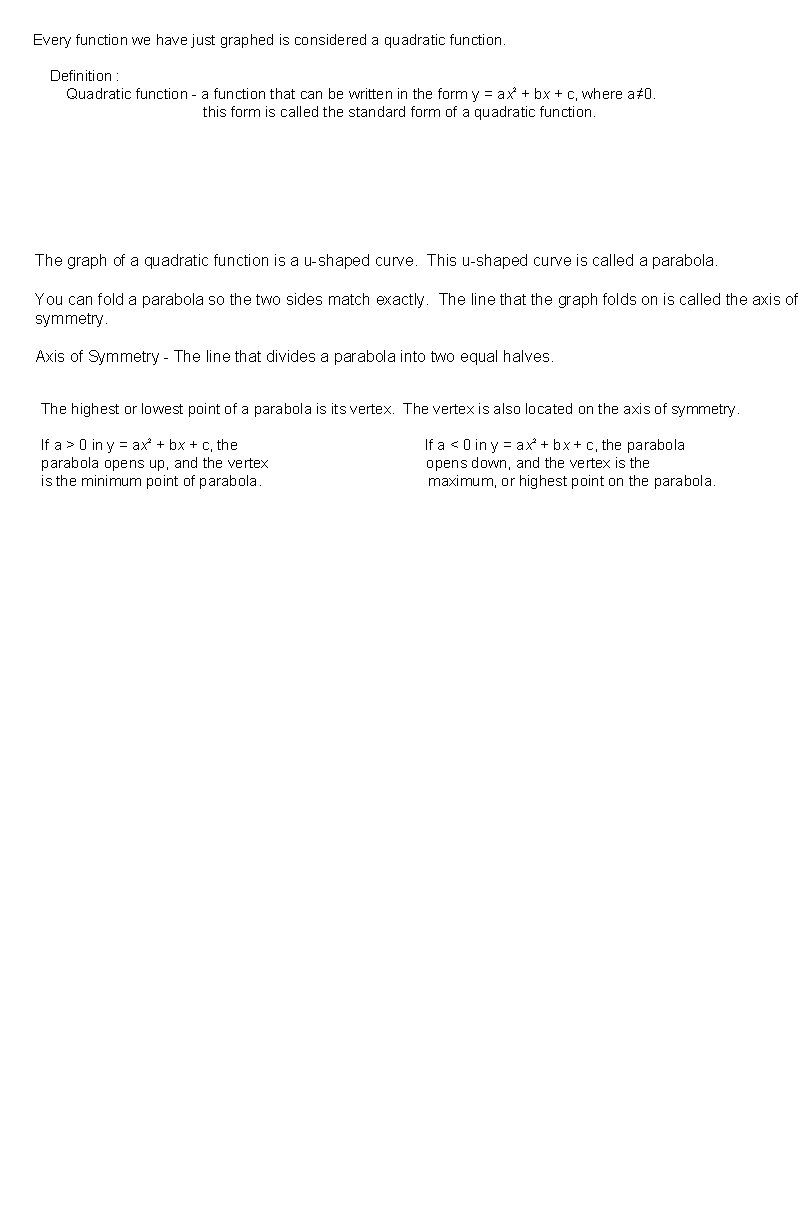
Every function we have just graphed is considered a quadratic function. Definition : Quadratic function - a function that can be written in the form y = ax 2 + bx + c, where a≠ 0. this form is called the standard form of a quadratic function. The graph of a quadratic function is a u-shaped curve. This u-shaped curve is called a parabola. You can fold a parabola so the two sides match exactly. The line that the graph folds on is called the axis of symmetry. Axis of Symmetry - The line that divides a parabola into two equal halves. The highest or lowest point of a parabola is its vertex. The vertex is also located on the axis of symmetry. If a > 0 in y = ax 2 + bx + c, the parabola opens up, and the vertex is the minimum point of parabola. If a < 0 in y = ax 2 + bx + c, the parabola opens down, and the vertex is the maximum, or highest point on the parabola.

Example 1: Identify a vertex. Identify the vertex of each graph: Now look at the check your understanding problems in the book. Work problems a and b. You can use the fact that a parabola is symmetric to graph it quickly. Symmetric means the same on both sides of a line of division(like the crease in a piece of paper folded in half). First find the coordinates of the vertex and some points on either side, then reflect or mirror those points on the other side of the axis of symmetry. For functions of the form y = ax 2 , the vertex is always at the origin. Example 2. Graphing y = ax 2 ke a table of values and graph y = ½x 2 Ma y = ½x 2 y x 0 0 ½ 1 2 2 8 4 Work the check your understanding problem for example 2.

The value of a, the coefficient of the x 2 term in a quadratic function, determines the width of a parabola and the direction that it opens(remember the graphs from the investigation). Example 3. Order the given functions from widest graph to narrowest graph. f(x) = -4 x 2, f(x) = ¼x 2, f(x) = x 2. Homework: pages 513 -514 problems 1 -13, 27 -30

Attachments
- Slides: 5