Section 1 6 Functions Definitions Relation Domain Range

Section 1. 6 Functions

Definitions Relation, Domain, Range, and Function The table describes a relationship between the variables x and y. This relationship is also described graphically. x 3 4 5 5 Section 1. 6 y 2 1 3 4 Lehmann, Intermediate Algebra, 3 ed Slide 2

Definitions Relation, Domain, Range, and Function Definition A relation is a set of ordered pairs. Definition The domain of a relation is the set of all values of the independent variable. Definition The range of the relation is the set of all values of the dependent variable. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 3

Definitions Relation, Domain, Range, and Function Think of a relation as a machine where: • x are the “inputs” -Each member of the domain is an input. • y are the “outputs” -Each member of the range is an output. Definition A function is a relation in which each input leads to exactly one output. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 4

Deciding whether an Equation Describes a Function Relation, Domain, Range, and Function Example Is the relation y = x +2 a function? Find the domain and the range of the relation. Solution Consider some input -output pairs. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 5

Deciding whether an Equation Describes a Function Relation, Domain, Range, and Function Solution Continued Each input leads to just one output–namely, the input increased by 2–so the relation y = x + 2 is a function. Domain • We can add 2 to any real number. • So, the domain is the set off all real numbers. Range • Output is two more than the input. • So, the range is the set off all real numbers. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 6

Deciding whether an Equation Describes a Function Relation, Domain, Range, and Function Example Is the relation a function? Solution • If x = 1, then • Input leads to two outputs: and • Therefore, the relation is not a function Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 7

Deciding whether an Equation Describes a Function Relation, Domain, Range, and Function Example Is the table a function? Solution • Consider the input x = 4 • Substitute 4 for x and solve for y: • Input x = 4 leads to two outputs: y = – 2 and y = 2 • So, the relation is not a function Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 8

Deciding whether a Table is a Function Relation, Domain, Range, and Function Example Is the relation a function? Solution • Input x = 1 leads to two outputs y = 3 and y = 5 • So, the relation is not a function. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed x 0 1 1 2 3 y 2 3 5 7 10 Slide 9

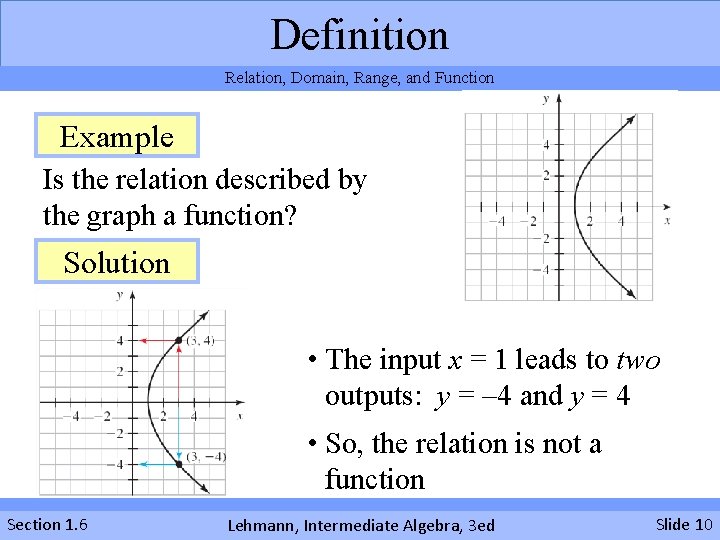
Definition Relation, Domain, Range, and Function Example Is the relation described by the graph a function? Solution • The input x = 1 leads to two outputs: y = – 4 and y = 4 • So, the relation is not a function Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 10

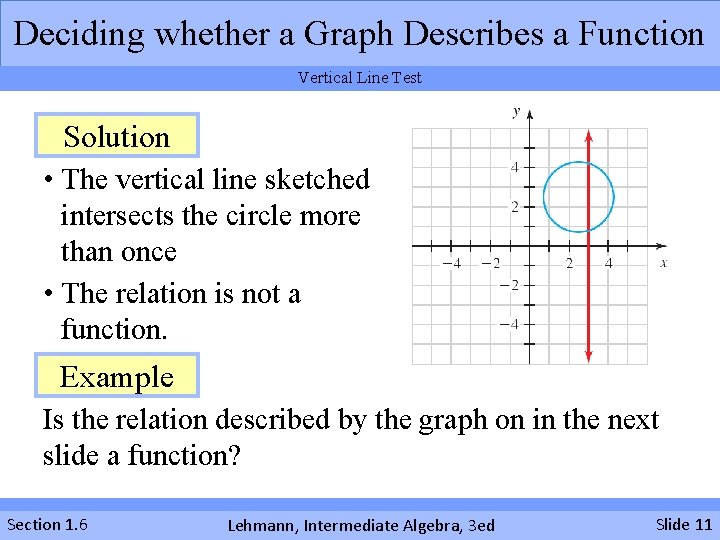
Deciding whether a Graph Describes a Function Vertical Line Test Solution • The vertical line sketched intersects the circle more than once • The relation is not a function. Example Is the relation described by the graph on in the next slide a function? Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 11

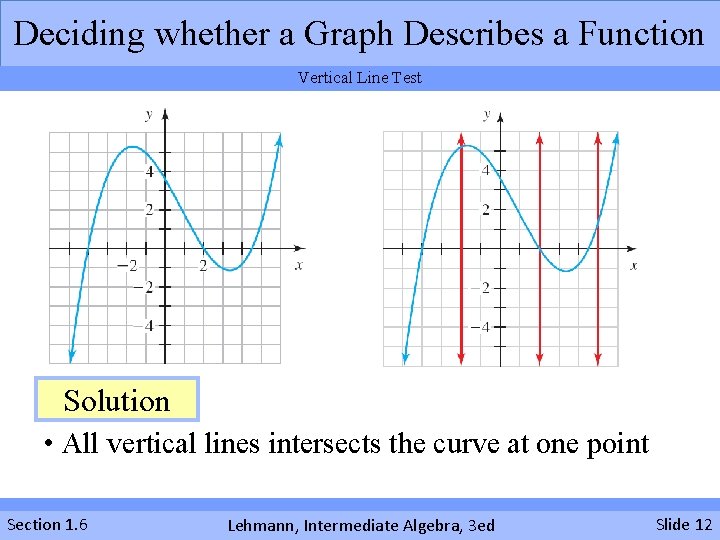
Deciding whether a Graph Describes a Function Vertical Line Test Solution • All vertical lines intersects the curve at one point Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 12

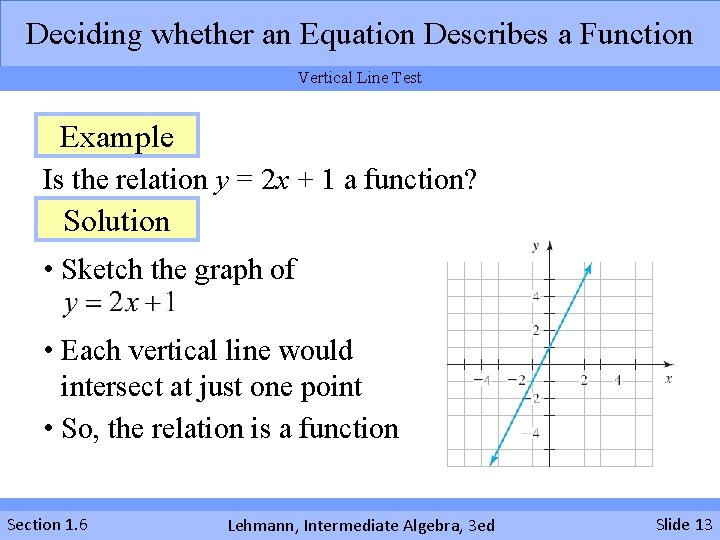
Deciding whether an Equation Describes a Function Vertical Line Test Example Is the relation y = 2 x + 1 a function? Solution • Sketch the graph of • Each vertical line would intersect at just one point • So, the relation is a function Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 13

Definition and Properties Linear Function Definition A linear function is a relation whose equation can be put into the form y = mx + b where m and b are constants. Properties of linear functions: 1. The graph of the function is a nonvertical line. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 14

Properties of Linear Functions Linear Function 2. The constant m is the slope of the line, a measure of the line’s steepness. 3. If m > 0, the graph of the function is an increasing line. 4. If m < 0, the graph of the function is a decreasing line. 5. If m = 0, the graph of the function is a horizontal line. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 15

Properties of Linear Functions Linear Function 6. If an input increases by 1, then the corresponding output changes by the slope m. 7. If the run is 1, the rise is the slope m. 8. The y-intercept of the line is (0, b). Since a linear equation of the form is a function, we know that each input leads to exactly output. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 16

Definition Rule of Four for Functions Definition We can describe some or all of the input–output pairs of a function by means of 1. an equation 2. a graph 3. a table, or 4. words. These four ways to describe input–output pairs of a function are known as the Rule of Four for functions. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 17

Describing a Function by Using the Rule of Four for Functions Example Is the relation a function? Solution Since is of the form (linear) function. , it is a Example List some input–output pairs of a table. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed by using Slide 18

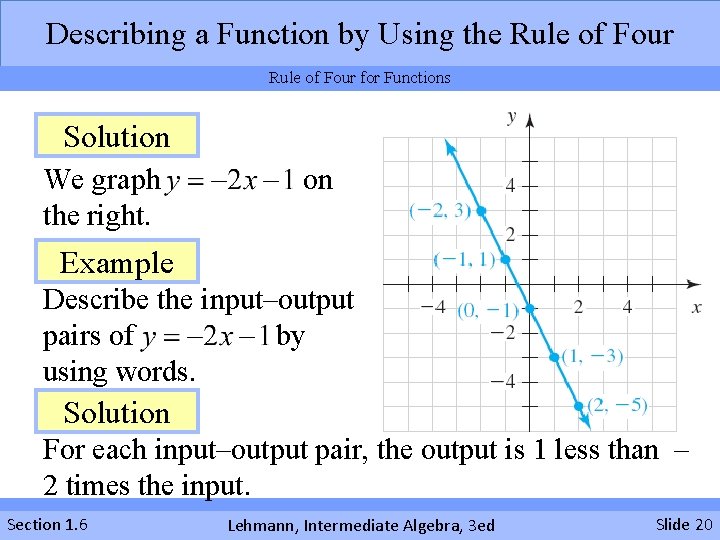
Describing a Function by Using the Rule of Four for Functions x Solution We list five input–output pairs of in the table on the right. Example Describe the input–output pairs of using a graph. Section 1. 6 – 2 – 1 0 1 2 Lehmann, Intermediate Algebra, 3 ed y – 2(– 2) – 1 = 3 – 2(– 1) – 1 = 1 – 2(0) – 1 = – 1 2(1) – 1 = – 3 – 2(2) – 1 = – 5 Slide 19

Describing a Function by Using the Rule of Four for Functions Solution We graph the right. on Example Describe the input–output pairs of by using words. Solution For each input–output pair, the output is 1 less than – 2 times the input. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 20

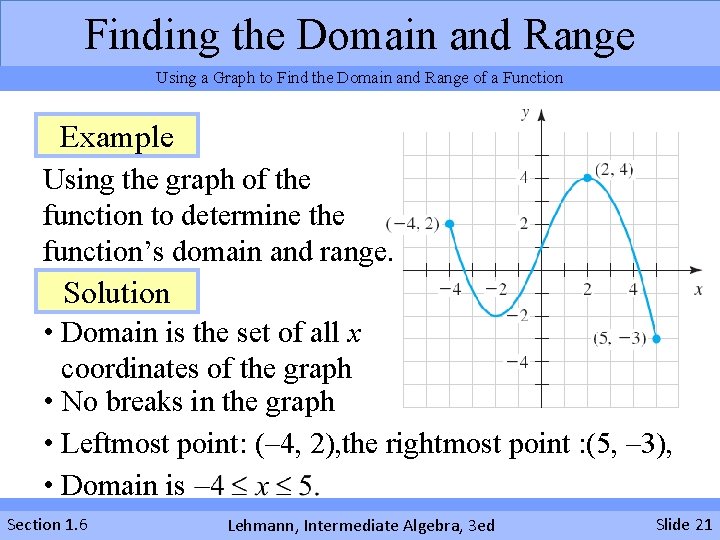
Finding the Domain and Range Using a Graph to Find the Domain and Range of a Function Example Using the graph of the function to determine the function’s domain and range. Solution • Domain is the set of all x coordinates of the graph • No breaks in the graph • Leftmost point: (– 4, 2), the rightmost point : (5, – 3), • Domain is Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 21

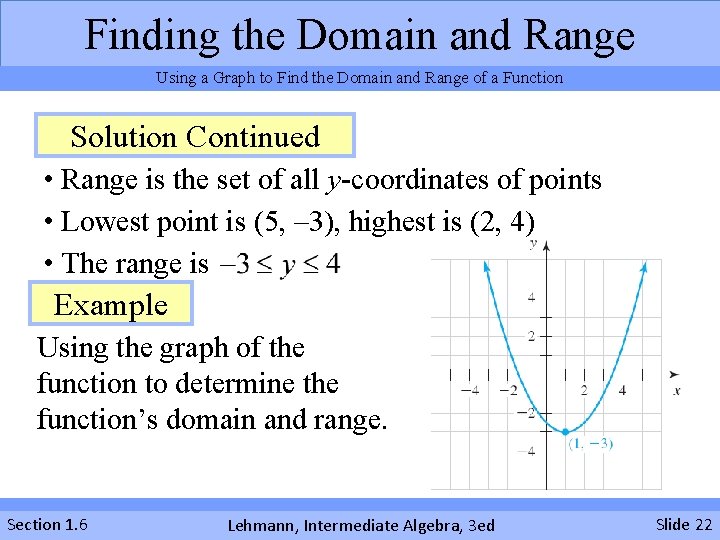
Finding the Domain and Range Using a Graph to Find the Domain and Range of a Function Solution Continued • Range is the set of all y-coordinates of points • Lowest point is (5, – 3), highest is (2, 4) • The range is Example Using the graph of the function to determine the function’s domain and range. Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 22

Finding the Domain and Range Using a Graph to Find the Domain and Range of a Function Solution Domain • Extends left and right indefinitely without breaks • Domain: set of all real numbers Range • Lowest point is (1, – 3) • Highest is indefinite without breaks • Range: Section 1. 6 Lehmann, Intermediate Algebra, 3 ed Slide 23