Section 1 4 Simplifying Algebraic expressions Evaluating an

Section 1. 4 Simplifying Algebraic expressions

Evaluating an expression • You will be given a value for one or all variables, then be asked to evaluate it. • Ex • Given x = 3 y = 4, evaluate 4 x – 2 y • Answer: 4(3) – 2(4) = 12 – 8 = 4

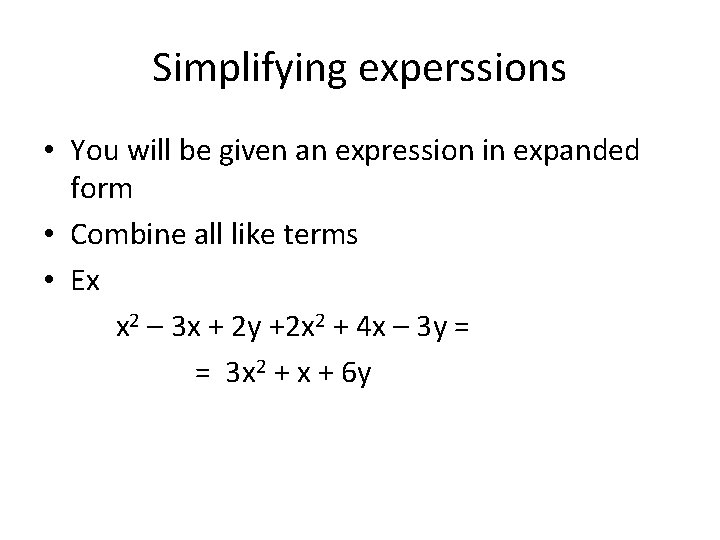
Simplifying experssions • You will be given an expression in expanded form • Combine all like terms • Ex x 2 – 3 x + 2 y +2 x 2 + 4 x – 3 y = = 3 x 2 + x + 6 y

More Complex example x(3 x – 2 y) – 3 xy + 2 x + 4 x 2 Distribute first = 3 x 2 – 2 xy – 3 xy + 2 x + 4 x 2 Combine like terms 7 x 2 – 5 xy +2 x

Homework • Pg 30 (1 -7, 15 -18, 27, 36, 38, 50, 51)

Section 1. 5 Properties of Exponents

• Exponents Example xa x is the base a is the exponent This means that x is multiplied by itself “a” times Ex: x 4 means (x)(x)

• Find the Following by hand 62 33 24 102

• Negative signs in the base number Find the following by using your calculator (-5)3 and -53 (-5)(-5) -[(5)(5)(5)] Do they work out to be the same number? Yes both are -125 Will this always be the case?

• Try these in your calculator (-4)3 and -43 (-4)(-4) -[(4)(4)(4)] Do they work out to be the same number? No both are 64, but one is – and one is + Brackets make a difference

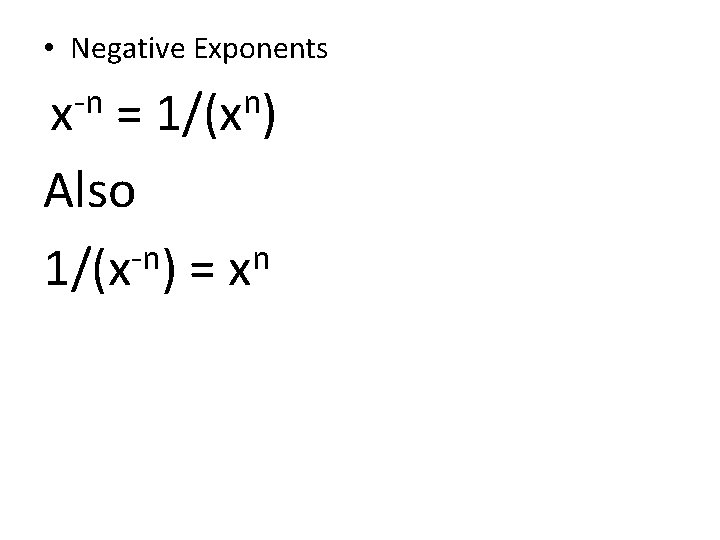
• Negative Exponents -n x n 1/(x ) = Also -n n 1/(x ) = x

• Try these examples [(4)(3)]-2 (12)-2 1/(122) 1/144 (3 -2)/(23) 1/[(32)(23)] 1/[(8)(9)] 1/72 1/(10 x)-3 (1)(10 x)3 (103)(x 3)

• Product of Powers • (xm)(xn)= xm+n where m & n are positive integers – in order for this to work the base of both numbers must be the same – The exponents can be different

• Examples (22)(23) = 22+3 = 25 = 32 (-12 mn 7)(6 m 3 n 2) = (-12)(6)(m)(m 3)(n 7)(n 2) = (72)(m 1+3)(n 7+2) = 72 m 4 n 9

• Try This (7 c 3 d 2)(4 c 2 d)(10 c 4 d 6) (7)(4)(10)(c 3)(c 2)(c 4)(d 2)(d)(d 6) (280)(c 3 +2+4)(d 2+1+6) 280 c 9 d 9

• Power of a Power (xm)n = xmn where m & n are positive integers Example (x 4)7 = x(4)(7) = x 28

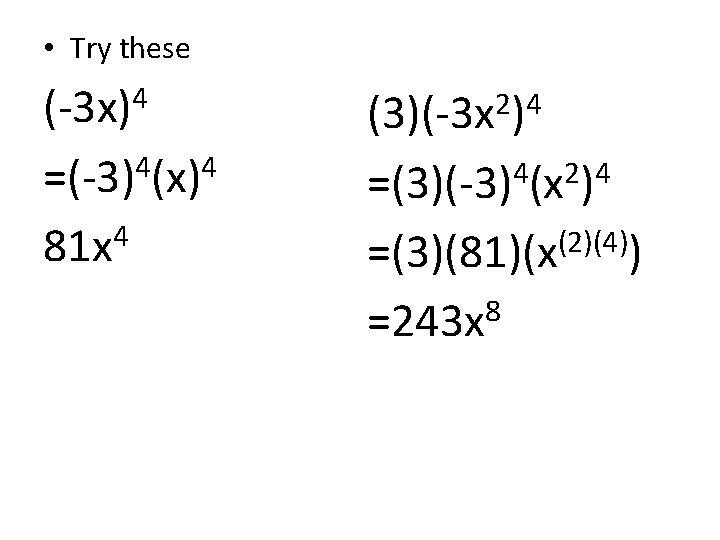
• Try these (-3 x)4 =(-3)4(x)4 4 81 x 2 4 (3)(-3 x ) 4 2 4 =(3)(-3) (x ) =(3)(81)(x(2)(4)) =243 x 8

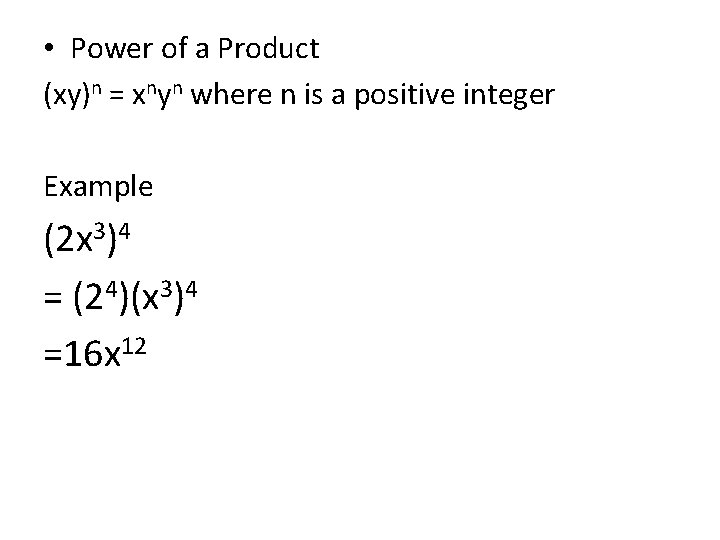
• Power of a Product (xy)n = xnyn where n is a positive integer Example (2 x 3)4 = (24)(x 3)4 =16 x 12

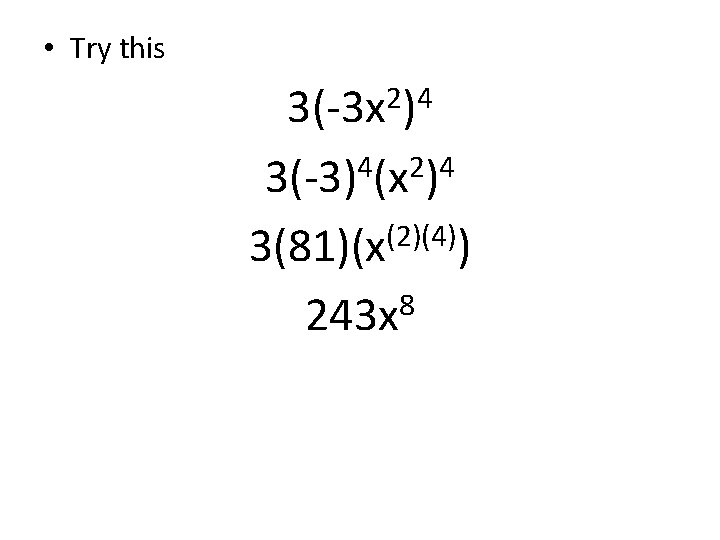
• Try this 3(-3 x 2)4 3(-3)4(x 2)4 (2)(4) 3(81)(x ) 8 243 x

• Power of a quotient (x/y)n = (xn)/(yn) where n is a positive integer Example [(x 2)/(y 6)]4 (x 2)4/(y 6)4 (x 8)/(y 24)

• Try this [(2 ab 2)/(3 c 3 d)]5 2 5 3 5 (2 ab ) /(3 c d) 5 5 (2)(5) 5 (3)(5) 5 (2 a b )/(3 c d ) (32 a 5 b 10)/(243 c 15 d 5)

• Quotients of Powers • (xm)/(xn) = xm – n • If m-n is negative then you must continue the simplification • Example (14 x 7)/(2 x 5) 7 x 7 – 5 7 x 2

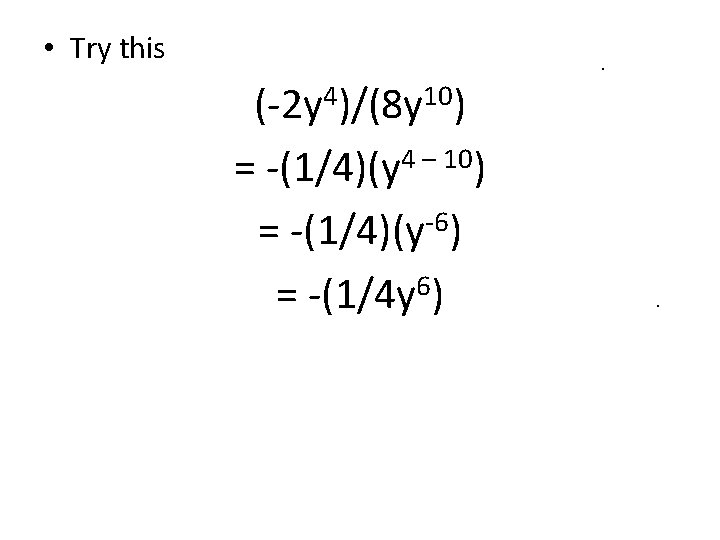
• Try this (-2 y 4)/(8 y 10) 4 – 10 = -(1/4)(y ) -6 = -(1/4)(y ) = -(1/4 y 6)

• Zero and Negative Exponents Use the properties of exponents to find the following. (23)/(23) By using properties of exponents we would subtract in this case so: 23 -3= 20 Also could be done this way: (23)/(23) = 8/8 =1

• • Definition For every number x, (not equal to 0) The following holds true x 0 = 1

____ x 10 (# between 1 and 10) a (can be positive or negative) Example 2. 3 x 106 = 2300. 2. 3 x 10 -6 =. 0000023 If there is a positive exponent the decimal moves right If there is a negative exponent the decimal moves left

• Going backwards • Express the following in scientific notation 645000 Would it be… 64. 5 x 104 Or 6. 45 x 105

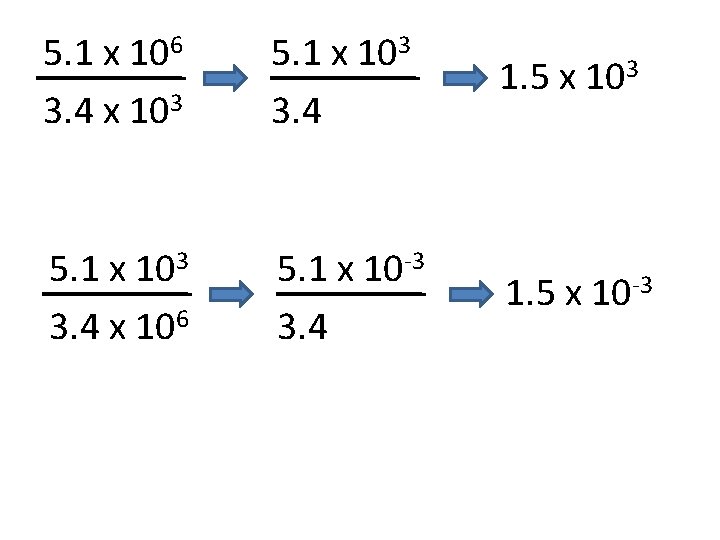
5. 1 x 106 3. 4 x 103 5. 1 x 103 3. 4 1. 5 x 103 5. 1 x 103 3. 4 x 106 5. 1 x 10 -3 3. 4 1. 5 x 10 -3

Homework • Pg 38 (1 -13 odd, 19, 24, 30, 31, 39, 58, 83 -86)