Section 1 4 Meaning of Slope for Equations

Section 1. 4 Meaning of Slope for Equations, Graphs, and Tables

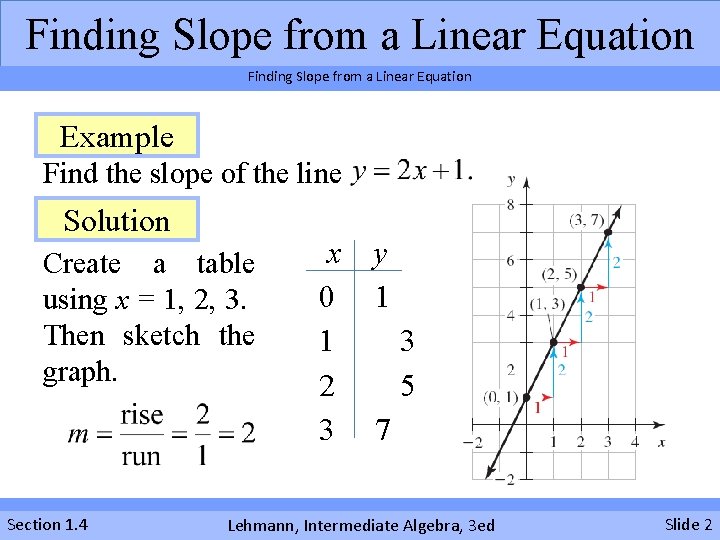
Finding Slope from a Linear Equation Example Find the slope of the line Solution Create a table using x = 1, 2, 3. Then sketch the graph. Section 1. 4 x 0 1 2 3 y 1 3 5 7 Lehmann, Intermediate Algebra, 3 ed Slide 2

Finding Slope from a Linear Equation Observations Note the following three observations about the slope of the line 1. The coefficient of x is 2, which is the slope. 2. If the run is 1, then the rise is 2. 3. As the value of x increases by 1, the value of y increases by 2. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 3

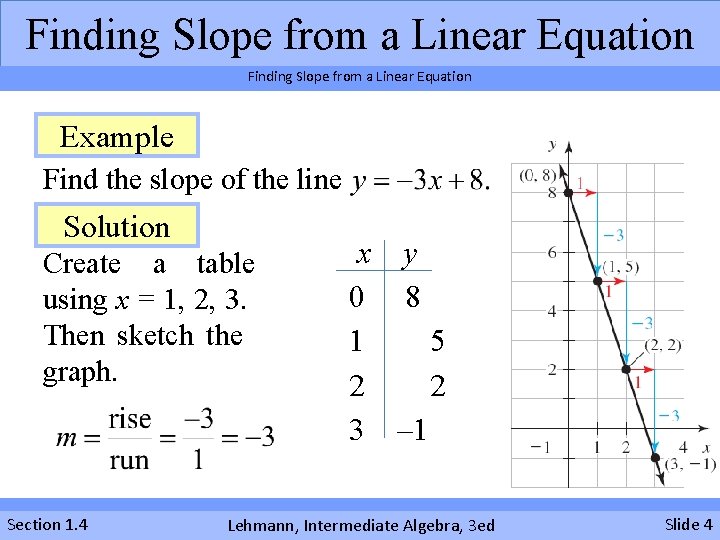
Finding Slope from a Linear Equation Example Find the slope of the line Solution Create a table using x = 1, 2, 3. Then sketch the graph. Section 1. 4 x y 0 8 1 5 2 2 3 – 1 Lehmann, Intermediate Algebra, 3 ed Slide 4

Finding Slope from a Linear Equation Property For a linear equation of the form slope of the line. , m is the Example Are the lines parallel, perpendicular, or neither? Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 5

Finding Slope from a Linear Equation Property • For the line the slope is • For the other equation we solve for y: Original Equation Add 10 x to both sides. Combine & rearrange terms Divide both sides by 12. Simplify. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 6

Finding Slope from a Linear Equation Solution Continued • For the line the slope is • Since the slopes are the same for both equations, the lines are parallel Graphing Calculator We use ZStandard followed by ZSquare to draw the line in the same coordinate system. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 7

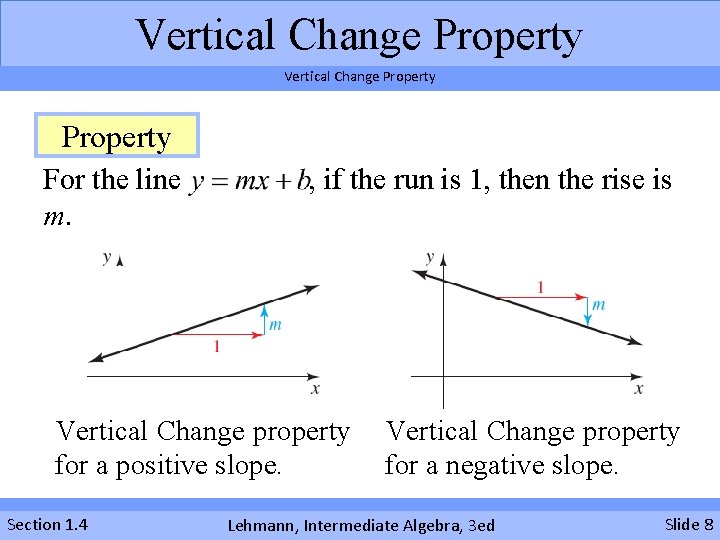
Vertical Change Property For the line m. , if the run is 1, then the rise is Vertical Change property for a positive slope. Section 1. 4 Vertical Change property for a negative slope. Lehmann, Intermediate Algebra, 3 ed Slide 8

Finding the y-intercept of a Linear Line Finding the y-Intercept of linear Equation Sketching Equations: • It’s helpful to know the y-intercept. • y-intercept has a x-value of 0. • Substitute x = 0 gives Property For a linear equation of the form intercept is (0, b). Section 1. 4 Lehmann, Intermediate Algebra, 3 ed , the y- Slide 9

Finding the y-intercept of a Linear Line Finding the y-Intercept of linear Equation Example What is the y-intercept of Solution • b is equal to 3, so the y-intercept is (0, 3) Definition If an equation of the form in slope-intercept form. Section 1. 4 , we say that it is Lehmann, Intermediate Algebra, 3 ed Slide 10

Graphing Linear Equations Example Sketch the graph of y = 3 x – 1. Solution • The y-intercept is (0, – 1) and the slope is To graph: 1. Plot the y-intercept, (0, 1). Section 1. 4 (continued) Lehmann, Intermediate Algebra, 3 ed Slide 11

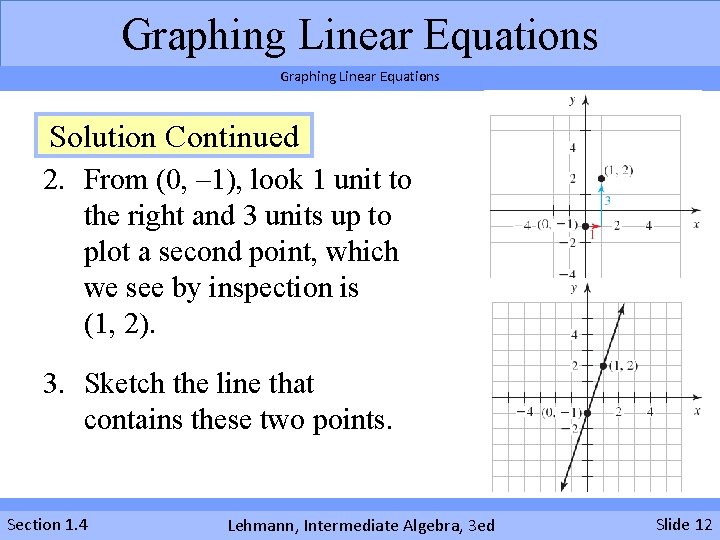
Graphing Linear Equations Solution Continued 2. From (0, – 1), look 1 unit to the right and 3 units up to plot a second point, which we see by inspection is (1, 2). 3. Sketch the line that contains these two points. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 12

Graphing Linear Equations Guidelines To sketch the graph of a linear equation of the form 1. Plot the y-intercept (0, b). 2. Use m = to plot a second point. 3. Sketch the line that passes through the two plotted points. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 13

Graphing Linear Equations Example Sketch the graph of 2 x + 3 y = 6. Solution First we rewrite into slope-intercept form: Original Equation Subtract 2 x from both sides. Combine & rearrange terms Divide both sides by 3. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 14

Graphing Linear Equations Solution Continued y-intercept: (0, 2) Slope: 1. Plot the y-intercept, (0, 2). 2. From the point (0, 2), look 3 units to the right and 2 units down to plot a second point, which we see by inspection is (3, 0). Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 15

Graphing Linear Equations Solution Continued 3. Then sketch the line that contains these two points. We can verify our result by checking that both (0, 2) and (3, 0) are solutions. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 16

Graphing Linear Equations Example 1. Determine the slope and the y-intercept of ax + by =c, where a, b, and c are constants and b is nonzero. 2. Find the slope and the y-intercept of the graph of 3 x + 7 y = 5. Solution First we rewrite into slope-intercept form: Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 17

Graphing Linear Equations Solution Continued Slope is Section 1. 4 and the y-intercept is Lehmann, Intermediate Algebra, 3 ed Slide 18

Graphing Linear Equations Solution Continued Given that ax + by = c in slope-intercept form is. , then given 3 x + 7 y = 5, we substitute. 3 for a, 7 for b and 5 for c. Thus, the slope, Section 1. 4 Lehmann, Intermediate Algebra, 3 ed . Slide 19

Slope Addition Property Example For the following sets, is there a line that passes through them? If so, find the slope of that line. Solution • Value of x increases by 1. • Value of y changes by – 3. • The slope is – 3. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 20

Slope Addition Property Solution Continued Set 2 • Value of x increases by 1. • Value of y changes by 5. So, the slope is 5. Set 3 • Value of x increases by 1. • Value of y does not change by the same value. Hence, not a line. Section 1. 4 Lehmann, Intermediate Algebra, 3 ed Slide 21