Section 1 2 Estimation Graphs and Mathematical Models

Section 1. 2 Estimation, Graphs and Mathematical Models Objectives 1. Using estimation techniques to arrive at an approximate answer to a problem. 2. Apply estimation techniques to information given by graphs. 3. Develop mathematical models that estimate relationships between variables. 1/10/2022 Section 1. 2 1

Estimation The process of arriving at an approximate answer to a question. Methods of Estimation • Rounding Numbers • Using Graphs • Using Mathematical Models 1/10/2022 Section 1. 2 2

Rounding Numbers 1. Look at the digit to the right of the digit where rounding is to occur. 2. a. If the digit to the right is 5 or greater, add 1 to the digit to be rounded. Replace all digits to the right by zeros. b. If the digit to the right is less than 5, do not change the digit to be rounded. Replace all digits to the right by zeros. 1/10/2022 Section 1. 2 3

Example 1 Rounding Whole numbers • Round the U. S. population (295, 734, 123) – To the nearest million: 295, 734, 123. The symbol ≈ means “approximately equal to” – To the nearest thousand: 295, 734, 123 1/10/2022 Section 1. 2 4

Rounding Decimal Numbers 1. Look at the digit to the right of the digit where rounding is to occur. 2. a. If the digit to the right is 5 or greater, add 1 to the digit to be rounded. Drop all digits to the right. b. If the digit to the right is less than 5, do not change the digit to be rounded. Drop all digits to the right. 1/10/2022 Section 1. 2 5

Example 2 Rounding Decimal Numbers: The number π (pi) • π is an irrational ( a non-terminating, non-repeating decimal) number used to represent the ratio between the circumference and diameter of a circle. The first seven digits of π are: 3. 141593. Round π: – To the nearest hundredth: 3. 141593 – To the nearest thousand: 3. 141593. 1/10/2022 Section 1. 2 6

Example 3: Estimation by Rounding • You purchased bread for $2. 59, detergent for $2. 17, a sandwich for $3. 65, an apple for $0. 47 and coffee for $5. 79. The total bill was $18. 67. Is this amount reasonable? • To check, round the cost of each • Item to the nearest dollar. This bill of $18. 67 seems high compared to the $15. 00 estimate. 1/10/2022 Section 1. 2 7

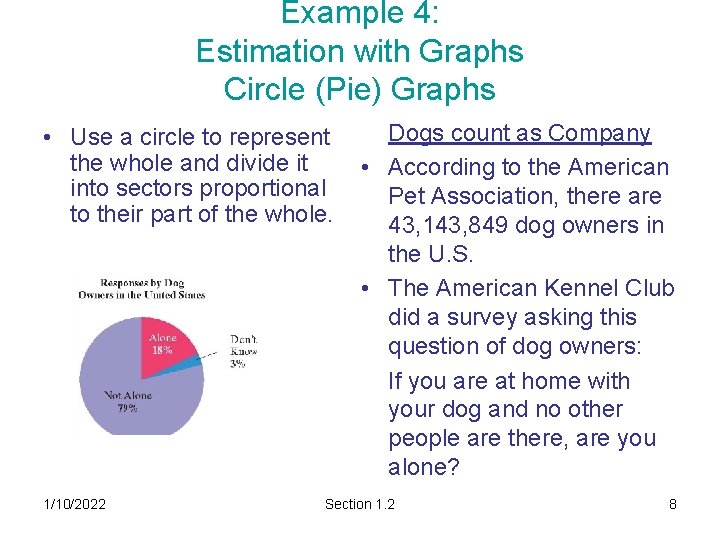
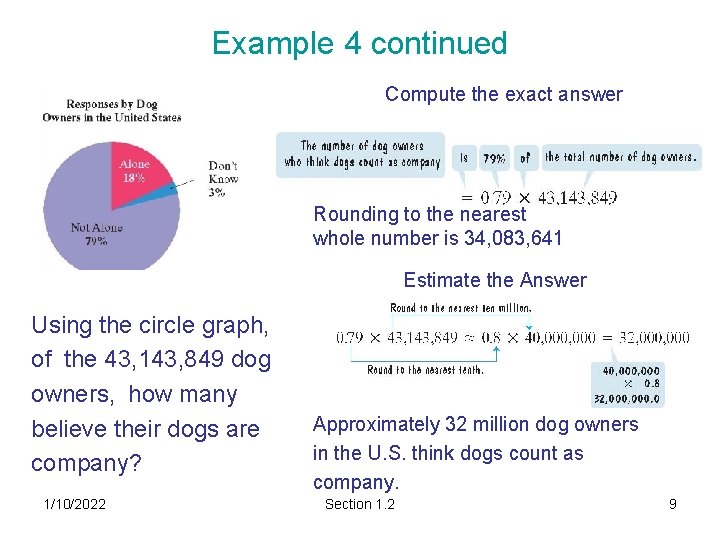
Example 4: Estimation with Graphs Circle (Pie) Graphs • Use a circle to represent the whole and divide it into sectors proportional to their part of the whole. 1/10/2022 Dogs count as Company • According to the American Pet Association, there are 43, 143, 849 dog owners in the U. S. • The American Kennel Club did a survey asking this question of dog owners: If you are at home with your dog and no other people are there, are you alone? Section 1. 2 8

Example 4 continued Compute the exact answer Rounding to the nearest whole number is 34, 083, 641 Estimate the Answer Using the circle graph, of the 43, 143, 849 dog owners, how many believe their dogs are company? 1/10/2022 Approximately 32 million dog owners in the U. S. think dogs count as company. Section 1. 2 9

Estimation with Graphs Bar Graphs • Bar graphs use a vertical or horizontal bar to represent each item. • The length of the bar determines the amount. • We can use bar graphs to make predictions. 1/10/2022 Section 1. 2 10

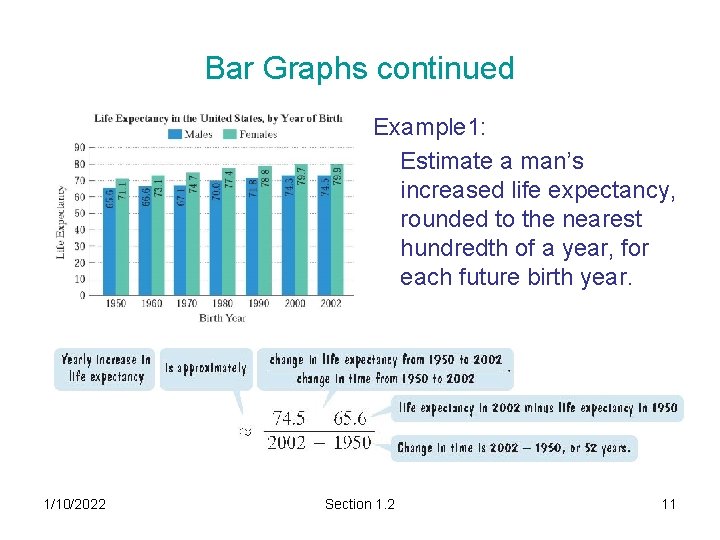
Bar Graphs continued Example 1: Estimate a man’s increased life expectancy, rounded to the nearest hundredth of a year, for each future birth year. 1/10/2022 Section 1. 2 11

Example 5 Bar Graphs Predict the life expectancy for a man born in 2020. The life expectancy for a man born in 2020 is approximately: The life expectancy each year is increasing by approximately 0. 17 years. 1/10/2022 Section 1. 2 12

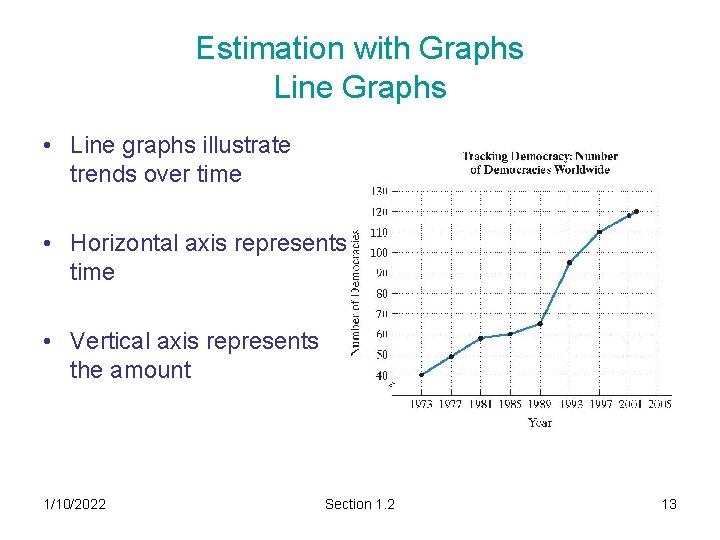
Estimation with Graphs Line Graphs • Line graphs illustrate trends over time • Horizontal axis represents time • Vertical axis represents the amount 1/10/2022 Section 1. 2 13

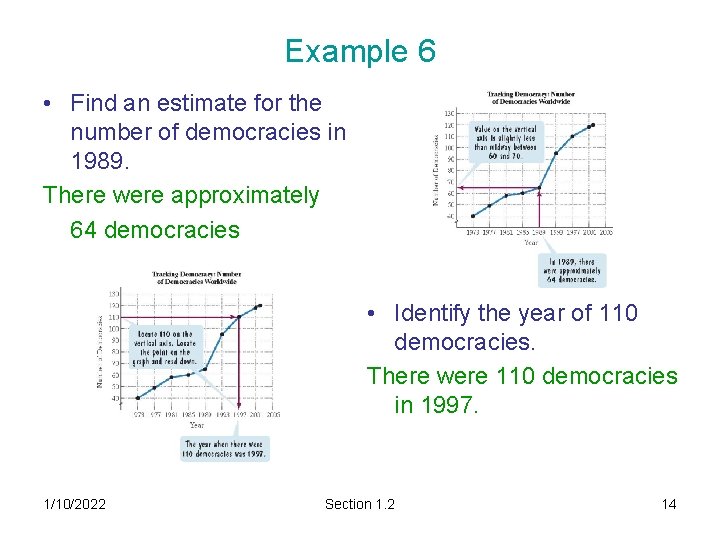
Example 6 • Find an estimate for the number of democracies in 1989. There were approximately 64 democracies • Identify the year of 110 democracies. There were 110 democracies in 1997. 1/10/2022 Section 1. 2 14

Example 7 Estimation with Mathematical Models • The process of finding formulas to describe realworld phenomena. • The graph on the next slide represents the median age of the U. S. population. • Create a mathematical model that estimates the median age, M of the U. S. population x years after 1970. 1/10/2022 Section 1. 2 15

Example 7 Continued • Find the yearly increase: The yearly increase ≈ 0. 25 • Use variables to obtain our model: The mathematical model estimates the median age, m, of the U. S population x years after 1970. 1/10/2022 Section 1. 2 16