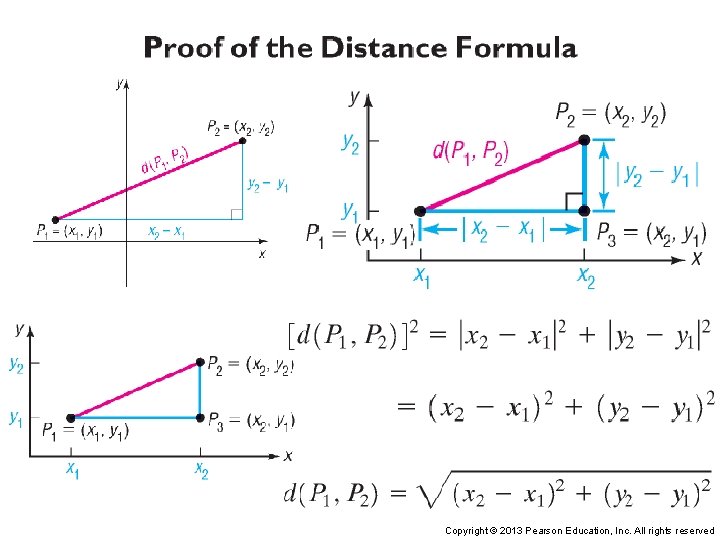
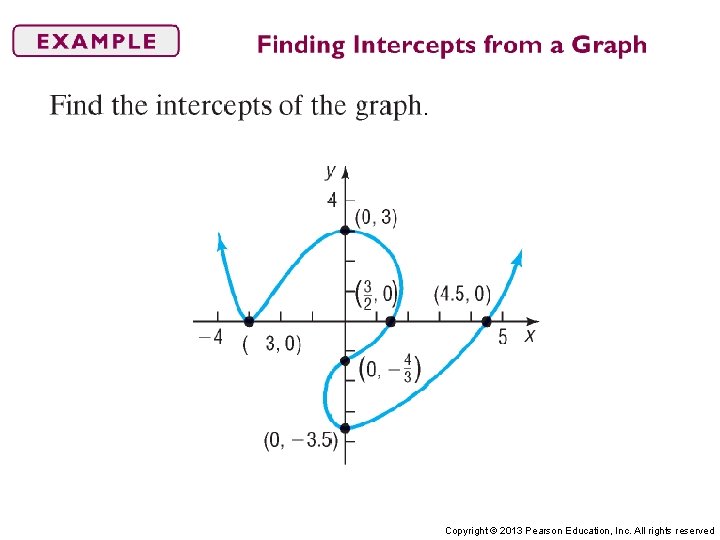
Section 1 1 The Distance and Midpoint Formulas
























- Slides: 43

Section 1. 1 The Distance and Midpoint Formulas; Graphing Utilities; Introduction to Graphing Equations Copyright © 2013 Pearson Education, Inc. All rights reserved

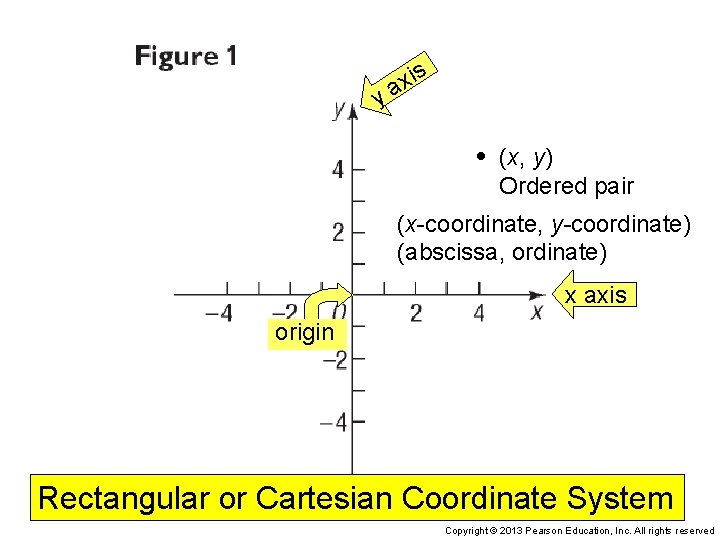
y is x a • (x, y) Ordered pair (x-coordinate, y-coordinate) (abscissa, ordinate) x axis origin Rectangular or Cartesian Coordinate System Copyright © 2013 Pearson Education, Inc. All rights reserved

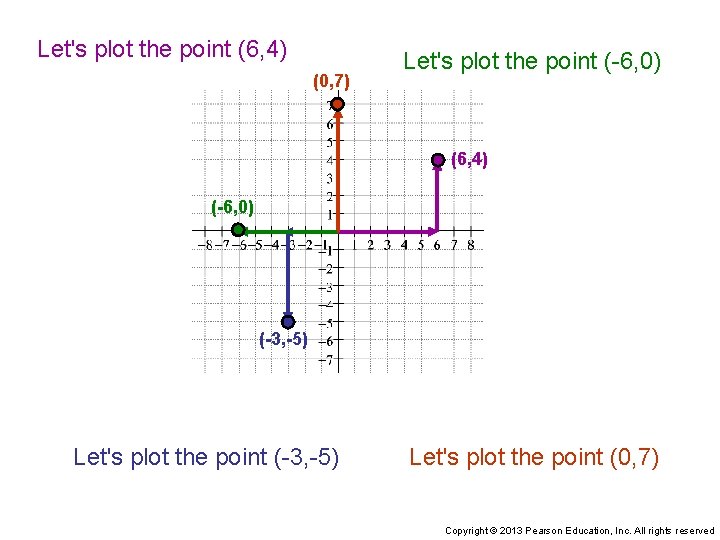
Let's plot the point (6, 4) (0, 7) Let's plot the point (-6, 0) (6, 4) (-6, 0) (-3, -5) Let's plot the point (0, 7) Copyright © 2013 Pearson Education, Inc. All rights reserved

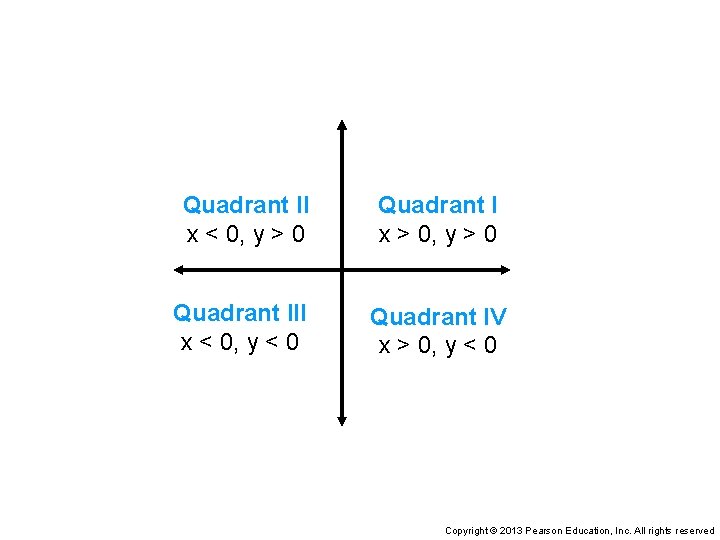
Quadrant II x < 0, y > 0 Quadrant I x > 0, y > 0 Quadrant III x < 0, y < 0 Quadrant IV x > 0, y < 0 Copyright © 2013 Pearson Education, Inc. All rights reserved

All graphing utilities (graphing calculators and computer software graphing packages) graph equations by plotting points on a screen. The screen of a graphing utility will display the coordinate axes of a rectangular coordinate system. Copyright © 2013 Pearson Education, Inc. All rights reserved

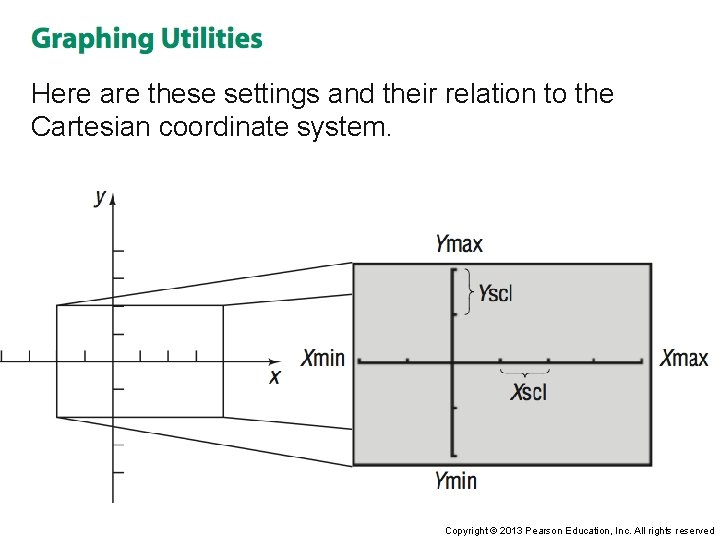
You must set the scale on each axis. You must also include the smallest and largest values of x and y that you want included in the graph. This is called setting the viewing rectangle or viewing window. Copyright © 2013 Pearson Education, Inc. All rights reserved

Here are these settings and their relation to the Cartesian coordinate system. Copyright © 2013 Pearson Education, Inc. All rights reserved

Finding the Coordinates of a Point Shown on a Graphing Utility Screen Find the coordinates of the point shown. Assume the coordinates are integers. Viewing Window 2 ticks to the left on the horizontal axis (scale = 1) and 1 tick up on the vertical axis (scale = 2), point is (– 2, 2) Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

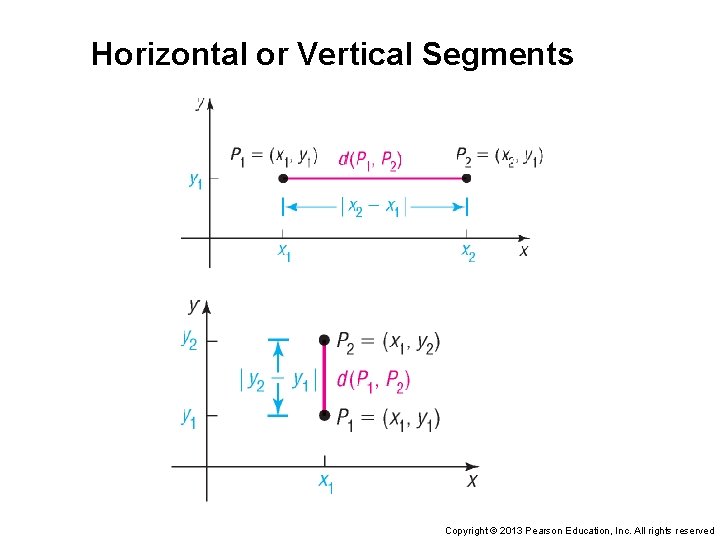
Horizontal or Vertical Segments Copyright © 2013 Pearson Education, Inc. All rights reserved

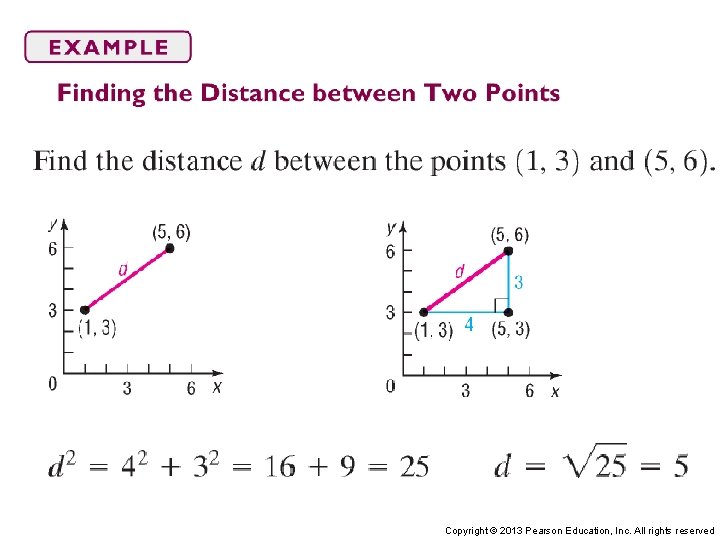
Find the distance d between the points (2, – 4) and (– 1, 3). Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

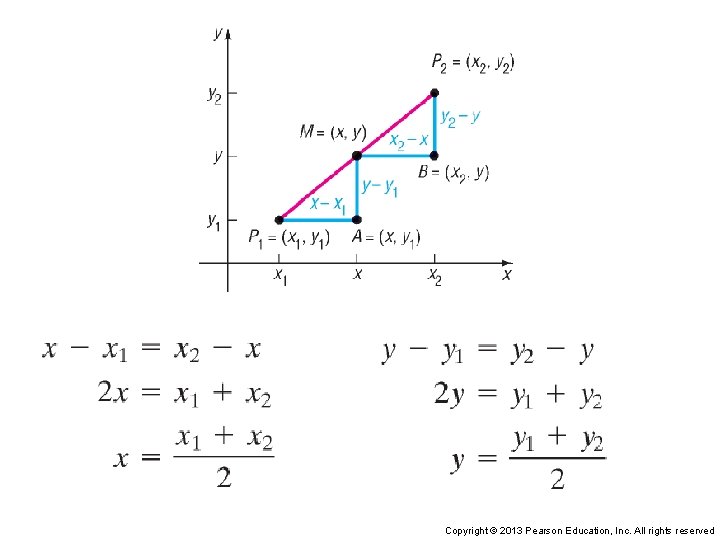
Find the midpoint of the line segment from P 1 = (4, – 2) to P 2 = (2, – 5). Plot the points and their midpoint. P 1 M P 2 Copyright © 2013 Pearson Education, Inc. All rights reserved

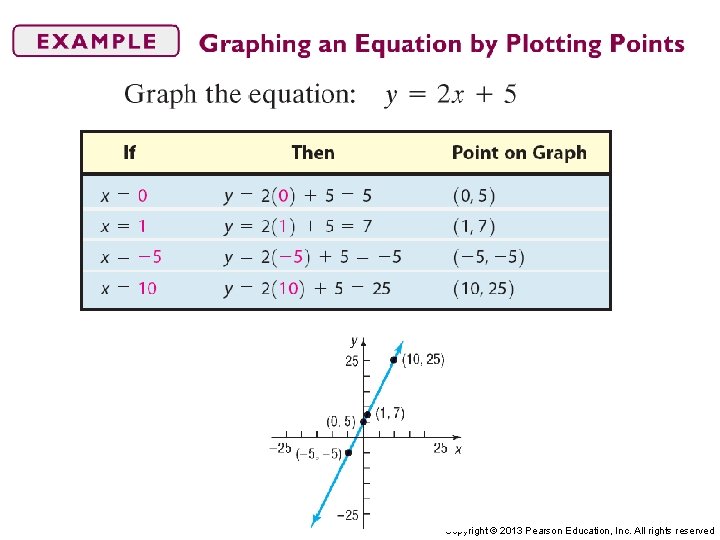
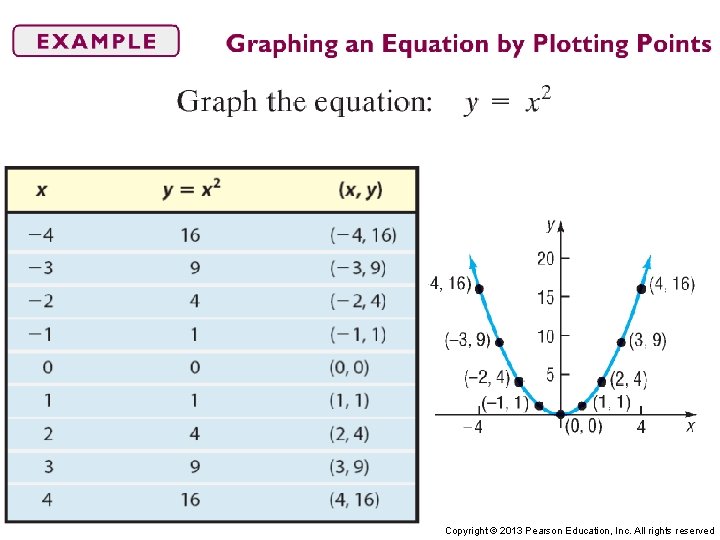
Graph Equations by Hand by Plotting Points Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

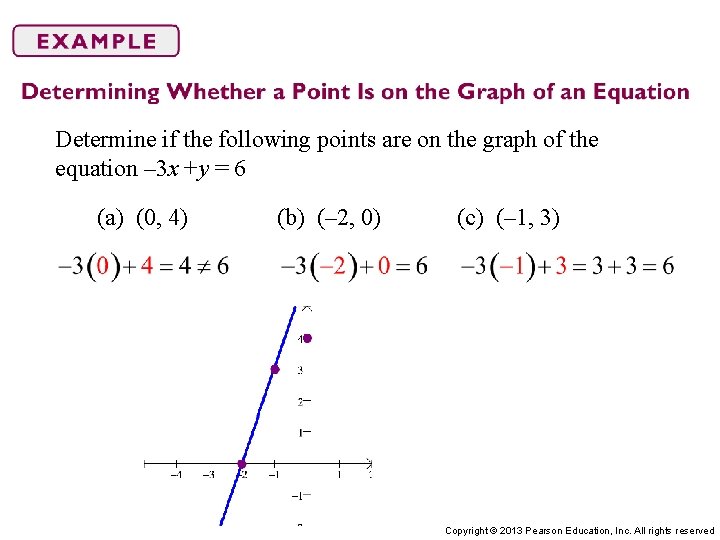
Determine if the following points are on the graph of the equation – 3 x +y = 6 (a) (0, 4) (b) (– 2, 0) (c) (– 1, 3) Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Graph Equations Using a Graphing Utility Copyright © 2013 Pearson Education, Inc. All rights reserved

To graph an equation in two variables x and y using a graphing utility requires that the equation be written in the form y = {expression in x}. If the original equation is not in this form, rewrite it using equivalent equations until the form y = {expression in x} is obtained. In general, there are four ways to obtain equivalent equations. Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Expressing an Equation in the Form y = {expression in x} Solve for y: 2 y + 3 x – 5 = 4 We replace the original equation by a succession of equivalent equations. Copyright © 2013 Pearson Education, Inc. All rights reserved

Graphing an Equation Using a Graphing Utility Use a graphing utility to graph the equation: 6 x 2 + 2 y = 36 Step 1: Solve for y. Copyright © 2013 Pearson Education, Inc. All rights reserved

Graphing an Equation Using a Graphing Utility Step 2: Enter the equation into the graphing utility. Step 3: Choose an initial viewing window. Copyright © 2013 Pearson Education, Inc. All rights reserved

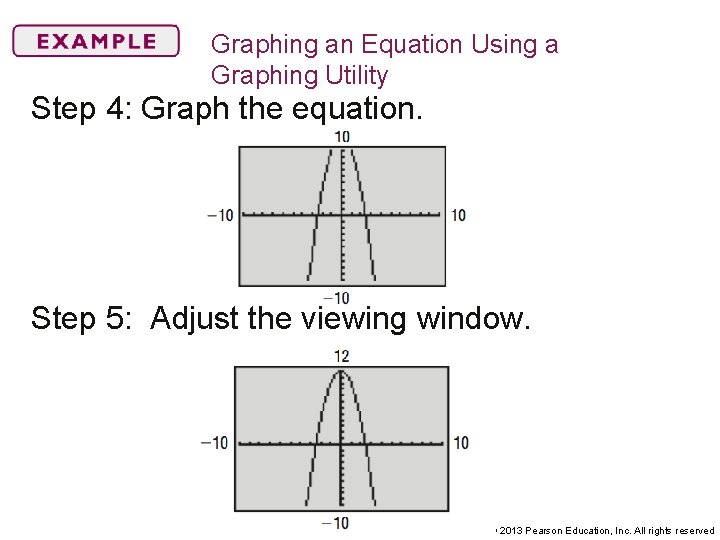
Graphing an Equation Using a Graphing Utility Step 4: Graph the equation. Step 5: Adjust the viewing window. Copyright © 2013 Pearson Education, Inc. All rights reserved

Use a Graphing Utility to Create Tables Copyright © 2013 Pearson Education, Inc. All rights reserved

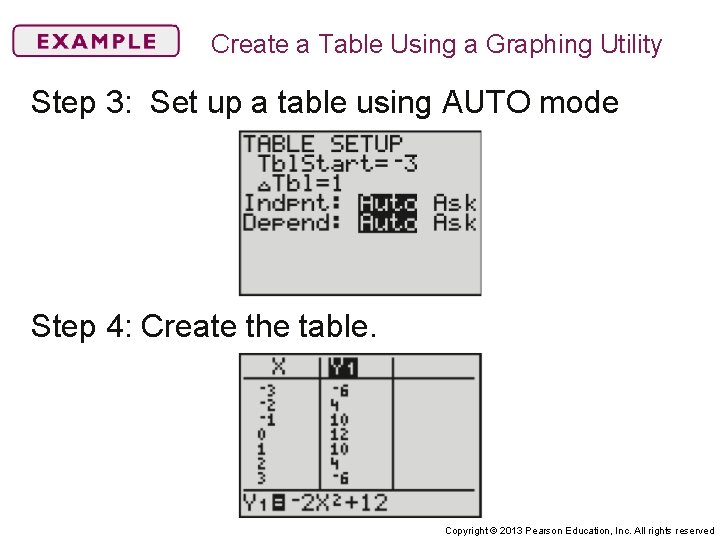
Create a Table Using a Graphing Utility Create a table that displays the points on the graph of 6 x 2 + 3 y = 36 for x = – 3, – 2, – 1, 0, 1, 2, and 3. Step 1: Solve for y: y = – 2 x 2 + 12 Step 2: Enter the equation into the graphing utility. Copyright © 2013 Pearson Education, Inc. All rights reserved

Create a Table Using a Graphing Utility Step 3: Set up a table using AUTO mode Step 4: Create the table. Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

Copyright © 2013 Pearson Education, Inc. All rights reserved

. Copyright © 2013 Pearson Education, Inc. All rights reserved

Use a Graphing Utility to Approximate Intercepts Copyright © 2013 Pearson Education, Inc. All rights reserved

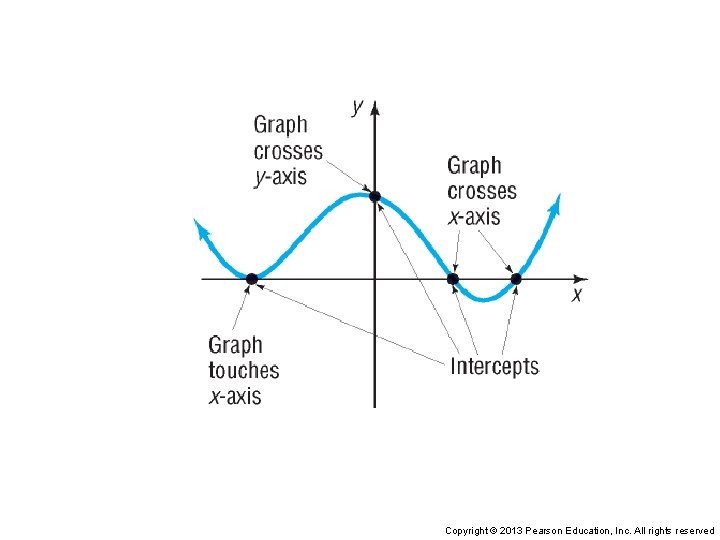
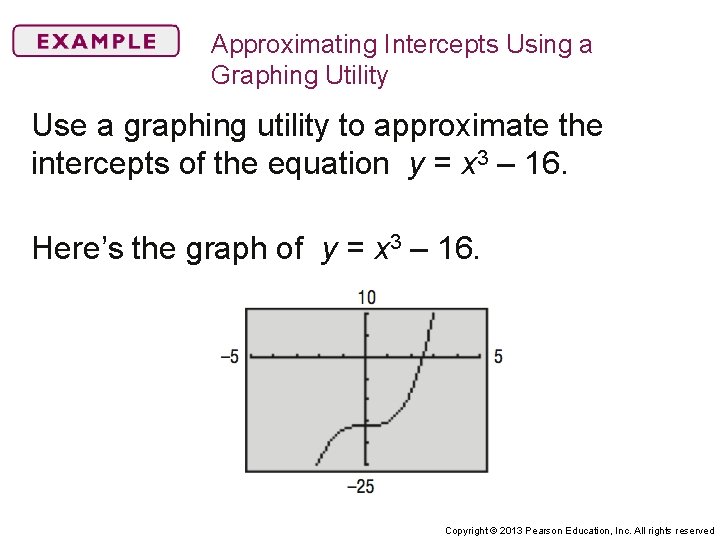
Approximating Intercepts Using a Graphing Utility Use a graphing utility to approximate the intercepts of the equation y = x 3 – 16. Here’s the graph of y = x 3 – 16. Copyright © 2013 Pearson Education, Inc. All rights reserved

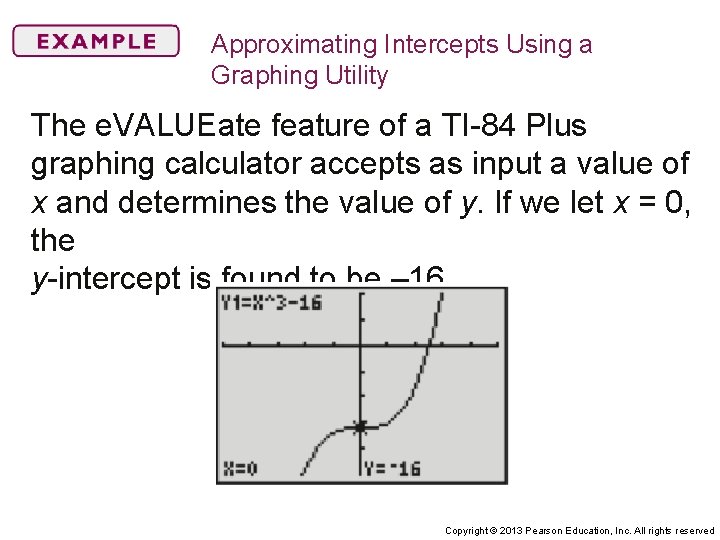
Approximating Intercepts Using a Graphing Utility The e. VALUEate feature of a TI-84 Plus graphing calculator accepts as input a value of x and determines the value of y. If we let x = 0, the y-intercept is found to be – 16. Copyright © 2013 Pearson Education, Inc. All rights reserved

Approximating Intercepts Using a Graphing Utility The ZERO feature of a TI-84 Plus is used to find the x-intercept(s). Rounded to two decimal places, the x-intercept is 2. 52. Copyright © 2013 Pearson Education, Inc. All rights reserved