Sect 7 7 Conservative Non Conservative Forces Conservative

Sect. 7. 7: Conservative & Non. Conservative Forces

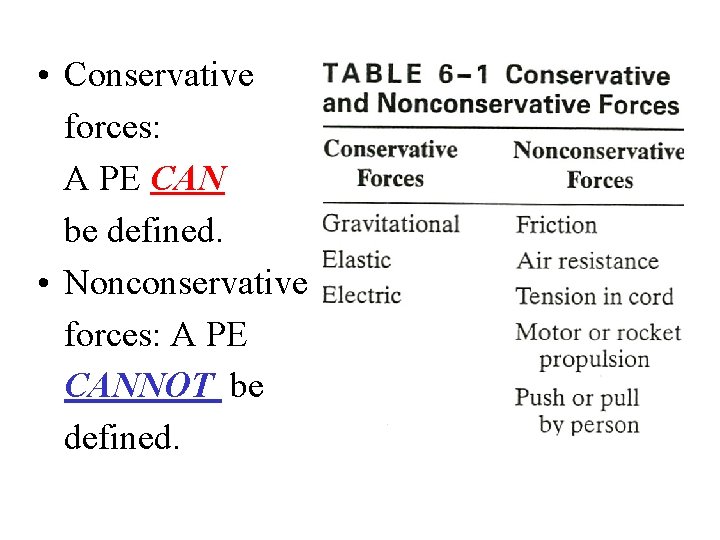
Conservative Forces • Conservative Force The work done by that force depends only on initial & final conditions & not on path taken between the initial & final positions of the mass. A PE CAN be defined for conservative forces • Non-Conservative Force The work done by that force depends on the path taken between the initial & final positions of the mass. A PE CANNOT be defined for non-conservative forces • The most common example of a non-conservative force is FRICTION

• Conservative forces: A PE CAN be defined. • Nonconservative forces: A PE CANNOT be defined.

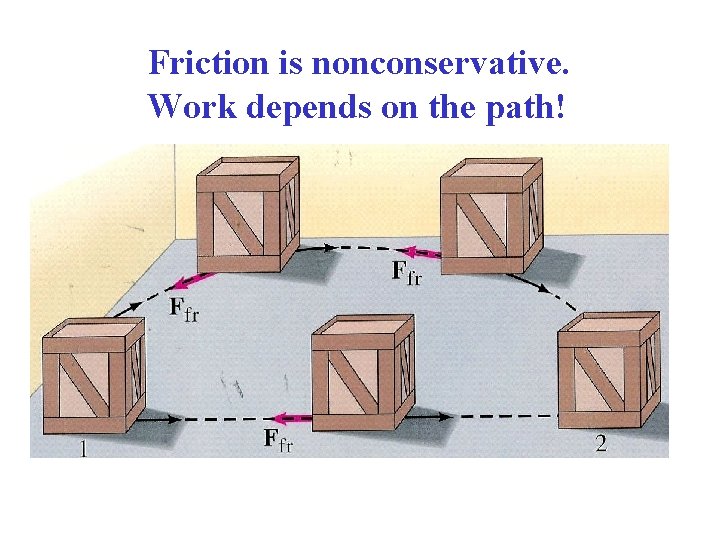
Friction is nonconservative. Work depends on the path!

• If several forces act (conservative & nonconservative): The total work done is: Wnet = WC + WNC WC = work done by conservative forces WNC = work done by non-conservative forces • The work-kinetic energy theorem still holds: Wnet = K • For conservative forces (by definition of PE U): OR: WC = - U KE = - U + WNC = K + U

In general, WNC = K + U Work done by non-conservative forces = total change in KE + total change in PE

Mechanical Energy & its Conservation • GENERAL: In any process, total energy is neither created nor destroyed. • Energy can be transformed from one form to another & from one body to another, but the total amount remains constant. Law of Conservation of Energy

• In general, we found: WNC = K + U • For the Special case of conservative forces only WNC = 0 K + U = 0 Principle of Conservation of Mechanical Energy • Note: This is NOT (quite) the same as the Law of Conservation of Energy! It is a special case of this law (where the forces are conservative)

Conservation of Mechanical Energy • For conservative forces ONLY! In any process K + U = 0 Conservation of Mechanical Energy • Define mechanical energy: E K+U Conservation of mechanical energy In any process, E = 0 = K + U OR: E = K + P = Constant In any process, the sum of the K and the U is unchanged (energy changes form from U to K or K to U, but the sum remains constant).

• Conservation of Mechanical Energy K + U = 0 E = K + U = Constant OR For conservative forces ONLY (gravity, spring, etc. ) • Suppose, initially: E = K 1 + U 1 & finally: E = K 2+ U 2 E = Constant K 1 + U 1 = K 2+ U 2 A powerful method of calculation!!

• Conservation of Mechanical Energy OR K + U = 0 E = K + U = Constant • For gravitational PE: Ug = mgy E = K 1 + U 1 = K 2+ U 2 (½)m(v 1)2 + mgy 1 = (½)m(v 2)2 + mgy 2 y 1 = Initial height, v 1 = Initial velocity y 2 = Final height, v 2 = Final velocity

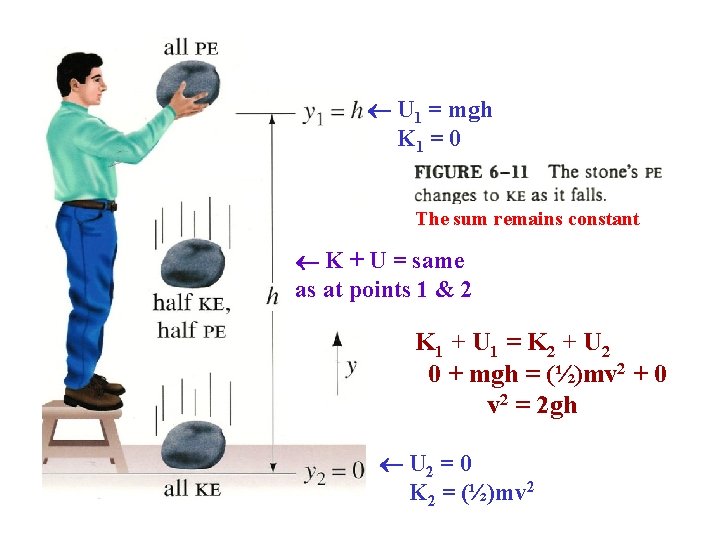
U 1 = mgh K 1 = 0 The sum remains constant K + U = same as at points 1 & 2 K 1 + U 1 = K 2 + U 2 0 + mgh = (½)mv 2 + 0 v 2 = 2 gh U 2 = 0 K 2 = (½)mv 2

Example • Energy “buckets” are for visualization only! Not real!! • Speed at y = 1. 0 m? • Conservation of mechanical energy! (½)m(v 1)2 + mgy 1 = (½)m(v 2)2 + mgy 2 (Mass cancels in equation!) y 1 = 3. 0 m, v 1 = 0 y 2 = 1. 0 m, v 2 = ? Find: v 2 = 6. 3 m/s PE only Part PE, part KE only

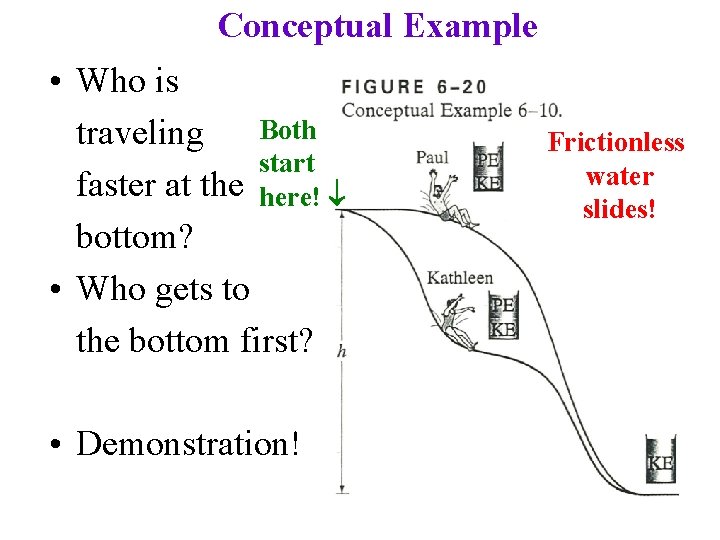
Conceptual Example • Who is Both traveling start faster at the here! bottom? • Who gets to the bottom first? • Demonstration! Frictionless water slides!

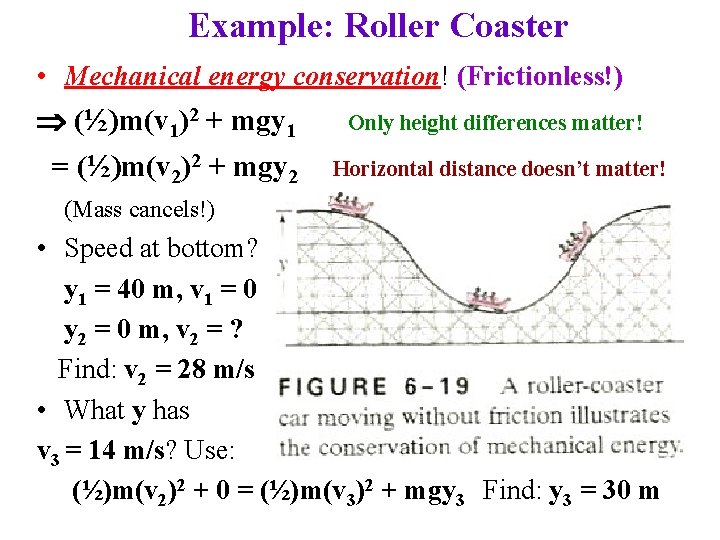
Example: Roller Coaster • Mechanical energy conservation! (Frictionless!) (½)m(v 1)2 + mgy 1 = (½)m(v 2)2 + mgy 2 Only height differences matter! Horizontal distance doesn’t matter! (Mass cancels!) • Speed at bottom? y 1 = 40 m, v 1 = 0 y 2 = 0 m, v 2 = ? Find: v 2 = 28 m/s • What y has v 3 = 14 m/s? Use: (½)m(v 2)2 + 0 = (½)m(v 3)2 + mgy 3 Find: y 3 = 30 m