Sect 7 3 Scalar Product of 2 Vectors

Sect. 7. 3: Scalar Product of 2 Vectors

Scalar Product of 2 Vectors • Pure math discussion for a short time. • We now know that work done by a constant force is: W = F||Δr = FΔr cosθ • Note that both F & Δr are vectors, while W is a scalar. • W has the mathematical form that mathematicians call the Scalar Product of Two Vectors • If A & B are vectors, their Scalar Product is defined as: A B ≡ AB cosθ

Scalar Product of two vectors A & B: A B ≡ AB cosθ • So, the work done by a constant force, W = FΔr cosθ, could be written as W ≡ F Δr • Basic math properties of the Scalar Product: 1. Commutative: A B = B A 2. Distributive: A (B + C) = A B + A C

Scalar Product of 2 Vectors Using Components Scalar Product: A B ≡ AB cosθ • From the discussion of vector components & unit vectors: A 3 dimensional vector V can be written as V = Vxi + Vyj + Vzk i, j, k are unit vectors along the x, y, z axes, Vx, Vy, Vz are the x, y, z components of V Unit vectors i, j, k are dimensionless & have length 1 • From scalar product definition & because the angles between i, j, k are all 90 [cos(90°) = 0, cos(0°) = 1] we can easily show: i i = j j = k k = 1 i j= i k = j k = 0

• For two 3 d vectors A & B using this notation: A = Axi + Ayj + Azk, B = Bxi + Byj + Bzk • Consider the scalar product of A & B in this form: A B = (Axi + Ayj + Azk) (Bxi + Byj + Bzk) • Rewriting this (long form, 9 terms!): A B = (Ax. Bx)(i i) + (Ax. By)(i j) + (Ax. Bz)(i k) + (Ay. Bx)(j i) + (Ay. By)(j j) + (Ay. Bz)(j k) + (Az. Bx)(k i) + (Az. By)(k j) + (Az. Bz)(k k) • Using i i = j j = k k = 1, i j= i k = j k = 0 gives A B = Ax. Bx + Ay. By + Az. Bz (1) This form will be convenient sometimes! • Also, consider the case where A = B. Then, (1) becomes: A A = Ax. Ax + Ay. Ay + Az. Az or A A = (Ax)2 + (Ay)2 + (Az)2 (2)

or A A = (Ax)2 + (Ay)2 + (Az)2 A A = |A|2 = square of length of A The scalar product of a vector with itself is the square of the length of that vector. • Examples 7. 2 & 7. 3

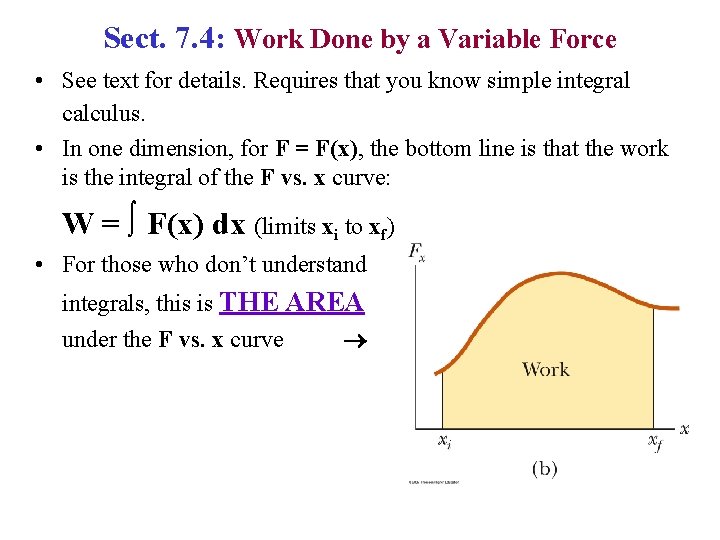
Sect. 7. 4: Work Done by a Variable Force • See text for details. Requires that you know simple integral calculus. • In one dimension, for F = F(x), the bottom line is that the work is the integral of the F vs. x curve: W = ∫ F(x) dx (limits xi to xf) • For those who don’t understand integrals, this is THE AREA under the F vs. x curve

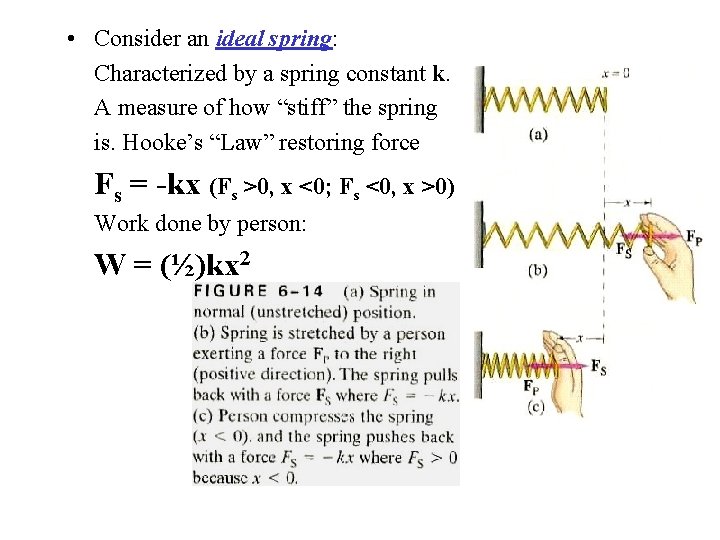
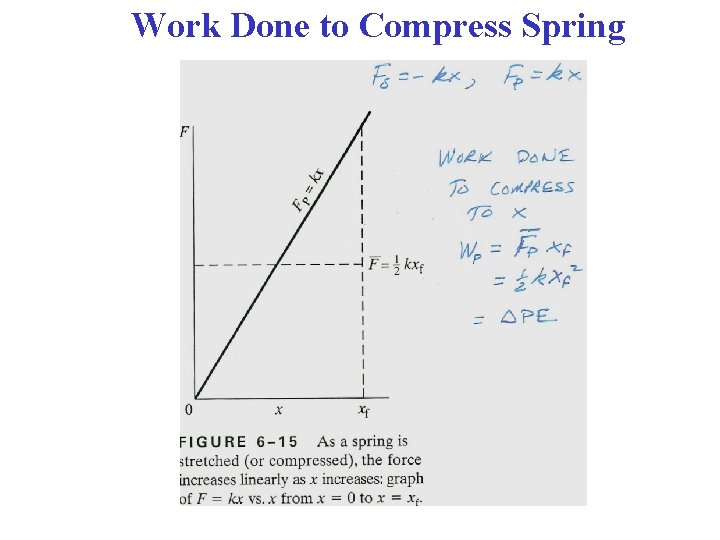
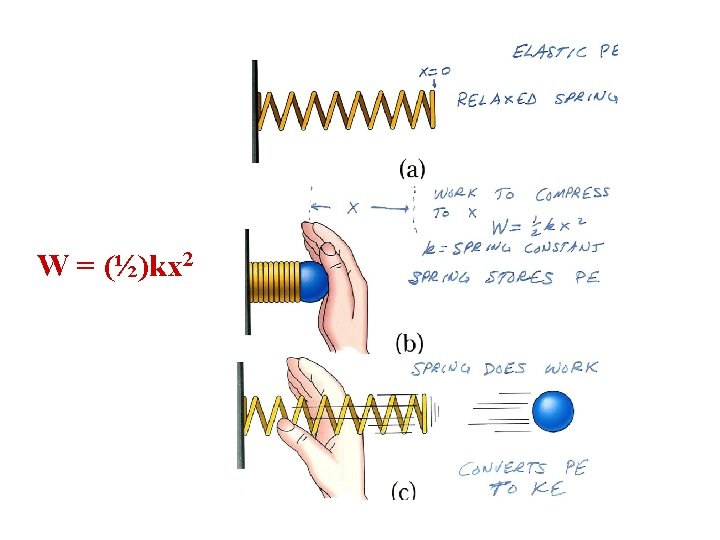
• Consider an ideal spring: Characterized by a spring constant k. A measure of how “stiff” the spring is. Hooke’s “Law” restoring force Fs = -kx (Fs >0, x <0; Fs <0, x >0) Work done by person: W = (½)kx 2

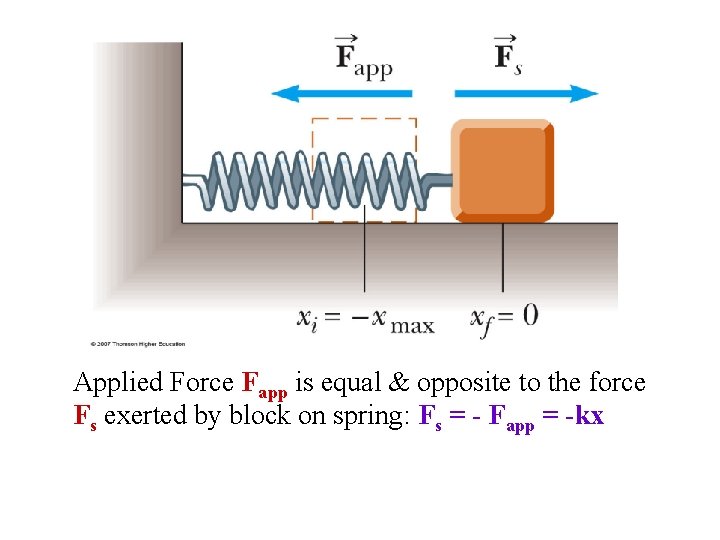
Applied Force Fapp is equal & opposite to the force Fs exerted by block on spring: Fs = - Fapp = -kx

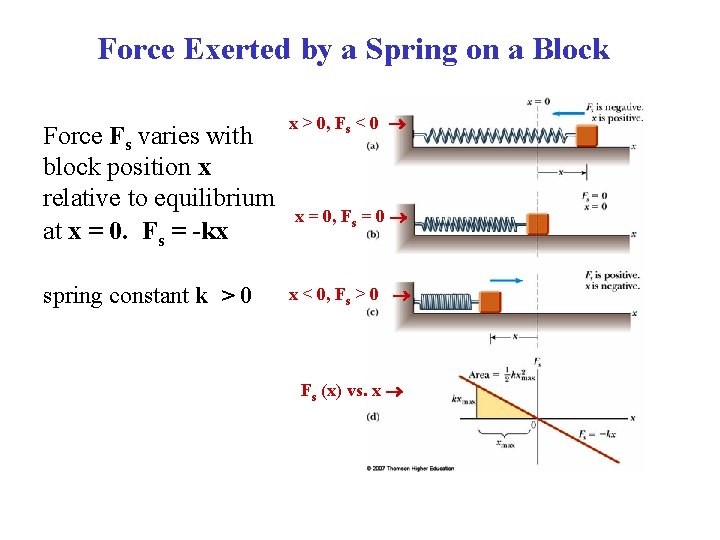
Force Exerted by a Spring on a Block Force Fs varies with block position x relative to equilibrium at x = 0. Fs = -kx spring constant k > 0 x > 0, Fs < 0 x = 0, Fs = 0 x < 0, Fs > 0 Fs (x) vs. x

Work Done to Compress Spring

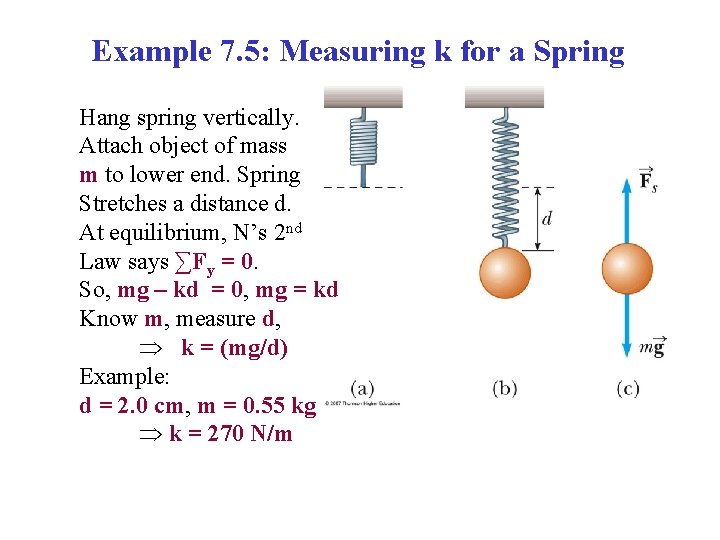
Example 7. 5: Measuring k for a Spring Hang spring vertically. Attach object of mass m to lower end. Spring Stretches a distance d. At equilibrium, N’s 2 nd Law says ∑Fy = 0. So, mg – kd = 0, mg = kd Know m, measure d, k = (mg/d) Example: d = 2. 0 cm, m = 0. 55 kg k = 270 N/m