Sect 4 4 Euler Angles Back to PHYSICS

Sect. 4. 4: Euler Angles • Back to PHYSICS! GOAL: Describe rigid body motion (especially rotations) with a Lagrangian formalism. What generalized coordinates to use? • General coord transformation, described by matrix A. Representation of A in terms of direction cosines of new axes with respect to old: aij cosθij: a 11 a 12 a 13 A a 21 a 22 a 23 a 31 a 32 a 33 • 9 aij , 6 orthogonality relns: aijaik = δj, k 3 indep functions of aij could be chosen as indep generalized coords. Choice of these is ~ arbitrary. Here, we discuss conventional choice: Euler Angles

• We found, for determinant of general orthogonal transformation A : |A| = 1 • In addition to orthogonality relns: aijaik = δj, k another requirement that matrix elements aij of must satisfy to describe rigid body motion: Must have |A| = +1 • Mathematically, |A| = -1 is allowed. However, PHYSICALLY, cannot describe rigid body motion with an A which has |A| = -1 • Proper Transformations Orthogonal transformations with |A| = +1 • Improper Transformations Orthogonal transformations with |A| = -1

• Discussion of why A with |A| = -1 cannot correspond to a physical rotation of a rigid body: • Consider a specific transformation described by -1 0 0 S= 0 -1 0 -1 Clearly, |S| = -1 0 0 -1 • Applying S to coords gives x = Sx xi = - xj (i = 1, 23) S Inversion transformation Changes sign of each component and changes right hand coord system into a left handed one.

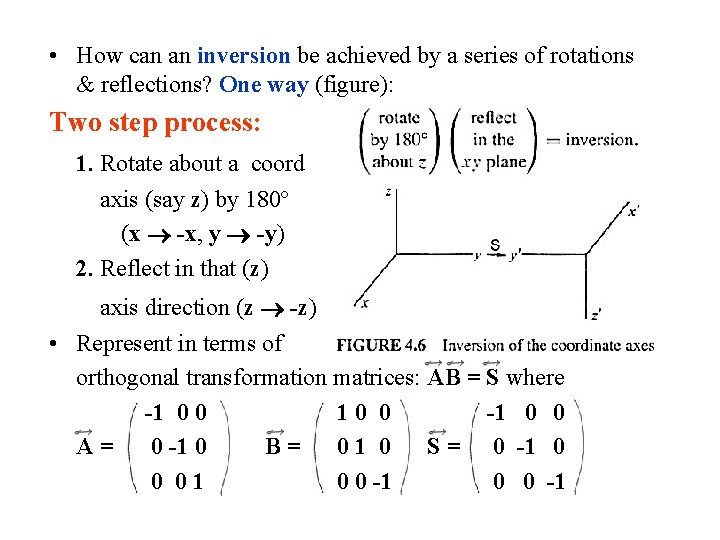
• How can an inversion be achieved by a series of rotations & reflections? One way (figure): Two step process: 1. Rotate about a coord axis (say z) by 180º (x -x, y -y) 2. Reflect in that (z) axis direction (z -z) • Represent in terms of orthogonal transformation matrices: AB = S where -1 0 0 10 0 -1 0 0 A= 0 -1 0 B= 01 0 S = 0 -1 0 0 01 0 0 -1

• Inversion: -1 0 0 S= 0 -1 0 0 0 -1 • Cannot get this by a rigid change of axes orientation! Inversion S can never correspond to a physical displacement of a rigid body. • Also true for ANY transformation A with |A| = -1. True because any A like this can be written A = A S where |A | = +1 (since |A| = |A ||S| = - |A |) Transformations A representing rigid body motion MUST have |A| = +1

• Goal: Describe motion of rigid bodies in a Lagrangian formulation. Seek 3 indep parameters (generalized coords) to specify rigid body orientation. Require resulting orthogonal transformation A have |A| = +1 • Once such generalized coords are found, write Lagrangian in terms of them. • No unique choices for these coords. Most common & useful: Euler (Eulerian) Angles.

Euler Angles • Can express general orthogonal transformation from one coord system (x, y, z) to another (x , y , z ) by three successive counterclockwise rotations, carried out in a specific sequence. Euler angles are then defined as the 3 rotation angles. – Convention for the choice of rotation sequence & of rotation angles is arbitrary. See text’s extensive discussion, p 151 & p 154, of this fact. See also footnote, p. 152. – Goldstein’s choice is a convention which is used in celestial mechanics, applied mechanics, solid state physics. For other conventions: See p. 152 & Appendix A.

• General transformation from (x, y, z) to (x , y , z ): 3 successive COUNTERCLOCKWISE rotations: 1. Rotate initial (x, y, z) by an angle about the z axis. Call new coords (ξ, η, ζ) “(xsi, eta, zeta)”. The orthogonal transformation which does this D. ξ Dx 2. Rotate (ξ, η, ζ) by an angle θ about the ξ axis. Call new coords (ξ , η , ζ ). The orthogonal transformation which does this C. ξ Cξ. The ξ axis is at intersection of the x-y and ξ - η planes “LINE OF NODES” 3. Rotate (ξ , η , ζ ) by an angle ψ about the ζ axis to produce (x , y , z ) coords. The orthogonal transformation which does this B. x Bξ

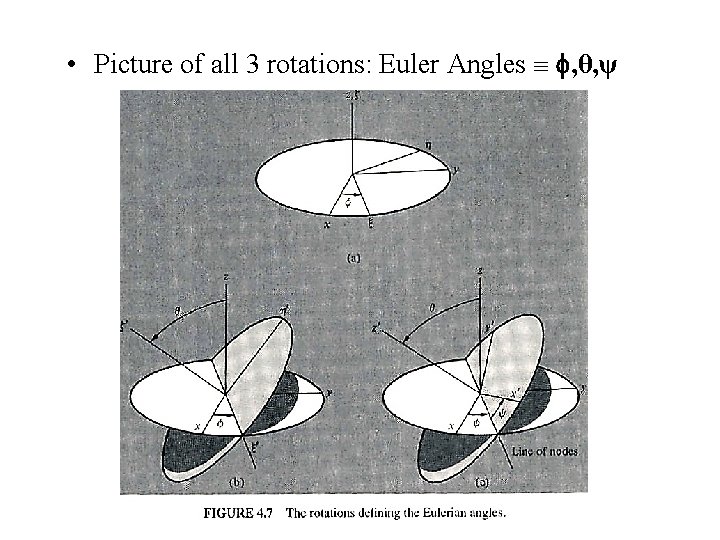
• Picture of all 3 rotations: Euler Angles , θ, ψ

• Express each successive rotation as an orthogonal transformation matrix. Multiply to get the total transformation. ξ Dx, ξ Cξ = CDx x Bξ = BCDx Or: x Ax where A BCD • Since we already know the form of the transformation matrix for rotation through one angle, it’s easy to write down the matrices D, C, B. Then, matrix multiply to get A = BCD

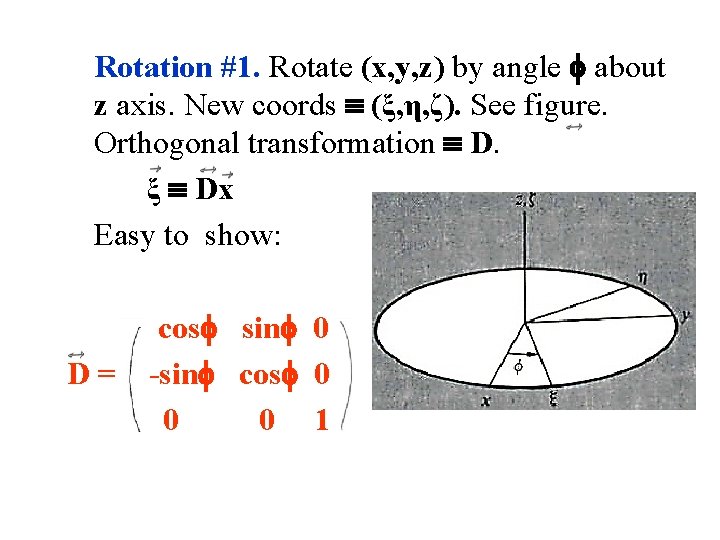
Rotation #1. Rotate (x, y, z) by angle about z axis. New coords (ξ, η, ζ). See figure. Orthogonal transformation D. ξ Dx Easy to show: D= cos sin 0 -sin cos 0 0 0 1

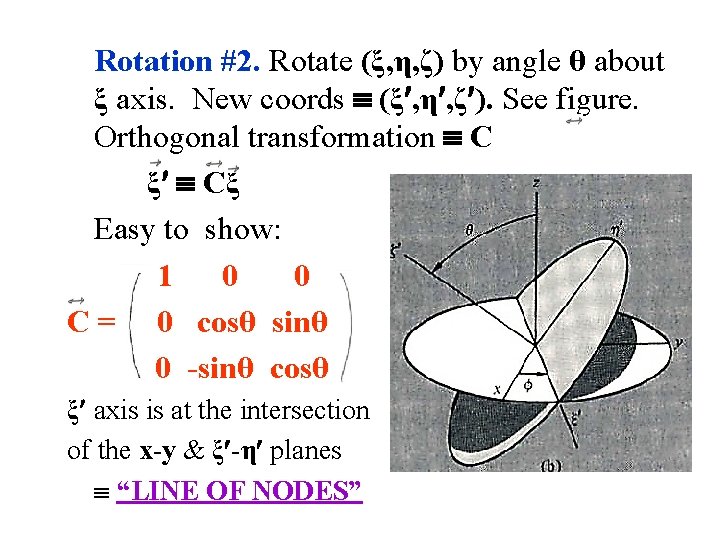
Rotation #2. Rotate (ξ, η, ζ) by angle θ about ξ axis. New coords (ξ , η , ζ ). See figure. Orthogonal transformation C ξ Cξ Easy to show: 1 0 0 C = 0 cosθ sinθ 0 -sinθ cosθ ξ axis is at the intersection of the x-y & ξ -η planes “LINE OF NODES”

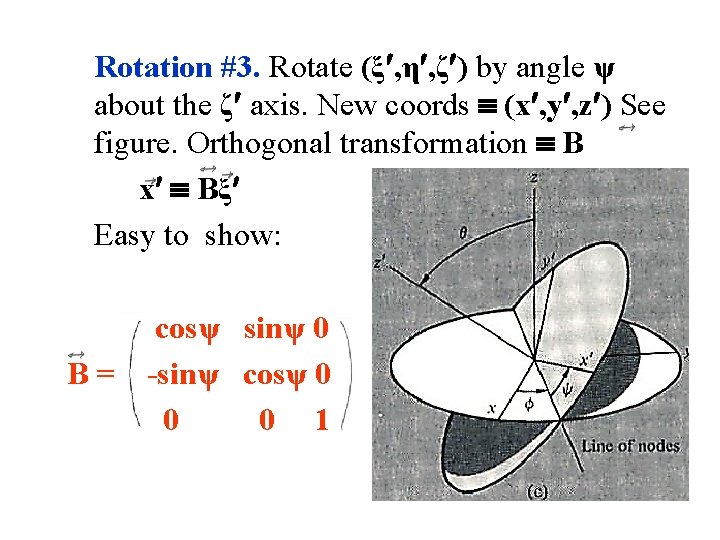
Rotation #3. Rotate (ξ , η , ζ ) by angle ψ about the ζ axis. New coords (x , y , z ) See figure. Orthogonal transformation B x Bξ Easy to show: B= cosψ sinψ 0 -sinψ cosψ 0 0 0 1

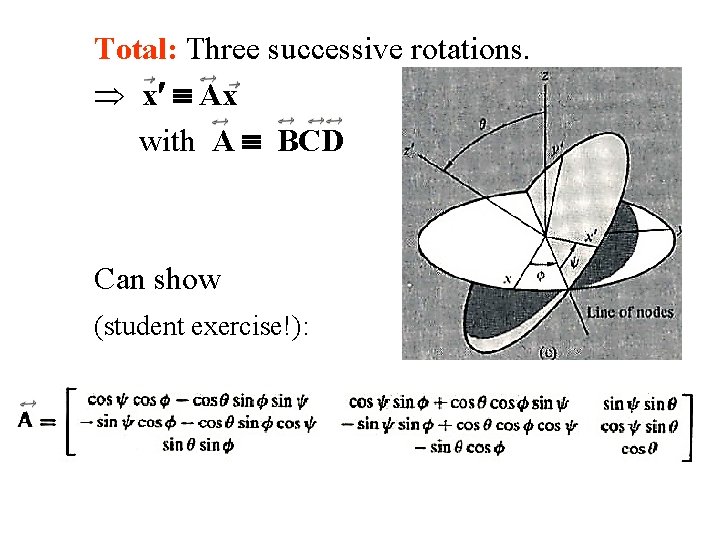
Total: Three successive rotations. x Ax with A BCD Can show (student exercise!):

Total: x Ax with Of course, the inverse transformation is: x A-1 x . Since, by earlier discussion A-1 = Ã Transpose of A, can get:

• Note: the sequence of rotations is ~ arbitrary. – Initial rotation: Could be taken about any of the 3 Cartesian axes. – 2 nd & 3 rd rotations: The only limitation = no 2 successive rotations can be about the same axis. 12 possible conventions to define Euler angles! (For right handed coord systems! If we include left handed coord systems, 12 more!) – The 2 most common ones: Differ in the axis choice for the 2 nd rotation (θ). Here: we rotate about intermediate x axis (ξ axis) “x convention” In QM often take this rotation about intermediate y axis (η axis) “y convention” – 3 rd convention (engineering): Used to describe the orientation of moving air (or space) craft. See p. 154 for discussion. See also Appendix A for more conventions!