Sect 2 4 HP for NonHolonomic Systems Can

Sect. 2. 4: HP for Non-Holonomic Systems • Can formally extend HP to include some types of non-holonomic systems. – Derivation of Lagrange’s Eqtns: Holonomic constraint requirement does not appear until last step. (When δqi are considered independent). • Holonomic constraints: m constraint eqtns: fα(q 1, q 2, …qn, t) = 0 (α = 1, . . m)

• Extension of HP to “semi-holonomic” systems for which constraint eqtns can be written: fα(q 1, q 2, …qn; q 1, q 2, …, qn) = 0 (α = 1, . . m) – Alternately, differential form: ∑kaαkdqk + aαtdt = 0 – Latter version is non-holonomic unless it can be integrated (unless it is an exact differential, in which case it is holonomic): aαk = ( fα/ qk) aαt = ( fα/ t)

• Consider “semi-holonomic” systems with constraints: fα(q 1, q 2, …qn; q 1, q 2, …qn) = 0 (α = 1, . . m) (1) • Multiply (1) by some unknown function λα = λα(q 1, q 2, …qn; t), & sum over all α ∑ α λ α fα = 0 (2) λα Lagrange’s undetermined multipliers • HP δ∫Ldt = 0 (limits t 1 < t 2) Combining with (2) gives: δ∫(L + ∑αλαfα) = 0 (3) (limits t 1 < t 2)

• HP δ∫(L + ∑αλαfα) = 0 (limits t 1 < t 2) (3) λα Lagrange’s undetermined multipliers • Follow the derivation from before of Lagrange’s Eqtns from HP & get: (d/dt)[( L/ qk)] - ( L/ qk) = Qk (4) (k = 1, 2, 3, … n) With generalized constraint force Qk is given as: Qk = ∑α{λα[( fα/ qk) - (d/dt)( fα/ qk)] - (dλα/dt)( fα/ qk)} (4) & (5): Lagrange’s Eqtns with undetermined multipliers (5)

• Recipe for Lagrange formalism with semiholonomic constraints: 1. For each constraint, introduce a multiplier λα = λα (t) 2. Apply Eqtns (4) & (5): (d/dt)[( L/ qk)] - ( L/ qk) = Qk (4) (j = 1, 2, 3, … n) Qk = ∑α{λα[( fα/ qk) - (d/dt)( fα/ qk)] - (dλα/dt)( fα/ qk)} (5) 3. Combine with m constraint eqtns: fα(qk; qk) = 0 Results Eqtns of motion for each qk PLUS eqtns which give the unknown multipliers λα

Physical Interpretation of λα • Qk = ∑α{λα[( fα/ qk) - (d/dt)( fα/ qk)] - (dλα/dt)( fα/ qk)} (5) • See text, Qk Generalized forces of constraint. From this formalism get eqtns of motion for qk PLUS generalized constraint forces. • Holonomic constraint eqtn of the form fα(q 1, q 2, …qn) = 0 (α = 1, . . m) is a special case of a semi-holonomic constraint eqtn: fα(q 1, q 2, …qn; q 1, q 2, …qn) = 0 (α = 1, . . m) Can also use this formalism with holonomic constraints. Useful if want to find constraint forces.

Example 1 • Particle with Lagrangian: L = (½)m[(x)2 + (y)2 + (z)2] - V(x, y, z) Subject to constraint: f(x, y, y) = x y + ky = 0 (1) • Eqtns of motion: mx +λy + ( V/ x) = 0 (2) my + λx -kλ + λx + ( V/ y) = 0 (3) mz + ( V/ z) = 0 (4) (1), (2), (3), (4): 4 coupled (differential) eqtns, 4 unknowns: x(t), y(t), z(t), λ(t)

• (1), (2), (3), (4): 4 coupled (differential) eqtns, 4 unknowns: x(t), y(t), z(t), λ(t) • Once solved (very messy math!), compute generalized constraint forces: Qk = λ[( f/ qk) - (d/dt)( f/ qk)] - (dλ/dt)( f/ qk) • Constraint eqtn: f(x, y, y) = x y + ky = 0 Qx = - λy; Qy = λ[k - x] - λx; Qz = 0

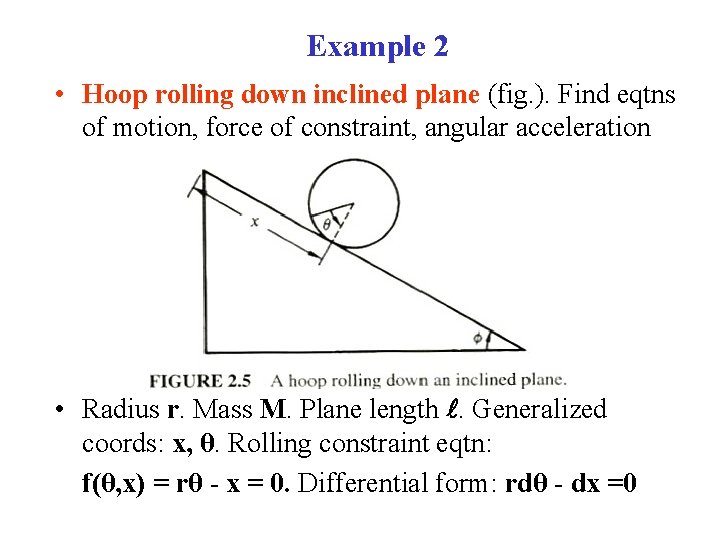
Example 2 • Hoop rolling down inclined plane (fig. ). Find eqtns of motion, force of constraint, angular acceleration • Radius r. Mass M. Plane length . Generalized coords: x, θ. Rolling constraint eqtn: f(θ, x) = rθ - x = 0. Differential form: rdθ - dx =0

• Constraint: rdθ - dx = 0 – Or, rθ - x = f (θ, x) = 0 Note: ( f/ θ) = r; ( f/ θ) = -1 ( f/ θ) = 0; ( f/ x) = 0 T = (½)M(x)2 + (½)Mr 2(θ)2 Moment of inertia of hoop = I = Mr 2 V = Mg( -x) sin L = T - V = (½)M(x)2 + (½)Mr 2(θ)2 - Mg( -x)sin • One Lagrange multiplier λ • Lagrange’s Eqtns: (k = r, θ) (d/dt)[( L/ qk)] - ( L/ qk) = Qk Qk = λ[( f/ qk) - (d/dt)( f/ qk)] - (dλ /dt)( f/ qk)

• rθ - x = 0 (1) – ( f/ θ) = r; ( f/ θ) = 0, ( f/ x) = -1, ( f/ x) = 0 Mx - Mg sin + λ = 0 (2) Mr 2θ - λr = 0 (3) • (1), (2), (3): 3 eqtns, 3 unknowns: x(t), θ(t), λ(t). Linear acceleration down the plane: x = (½)gsin Angular acceleration of hoop: θ = (½)(gsin )/r = (x/r) Lagrange multiplier: λ = (½)Mgsin = “Normal force” between hoop & plane

Lagrange multiplier: λ = (½)Mgsin • Generalized forces of constraint: Qx = λ[( f/ x) - (d/dt)( f/ x)] - (dλ/dt)( f/ x) = -λ = -(½)Mgsin = “Normal force” between the hoop & the plane Q = λ[( f/ θ) - (d/dt)( f/ θ)] - (dλ/dt)( f/ θ) = λr = -(½)Mgsin = Torque about hoop axis produced by the “normal force” between the hoop & the plane

Example from Marion • A mass m starts from rest on top of a frictionless hemisphere, radius a (fig. ). Find: Eqtns of motion, force of constraint & angle at which m leaves the hemisphere. On the blackboard!

Solution, page 1!!

Solution, page 2!!