Sect 13 4 The Gravitational Field Gravitational Field

Sect. 13. 4: The Gravitational Field

Gravitational Field • A Gravitational Field , exists at all points in space. • If a particle of mass m is placed at a point where the gravitational field is , it experiences a force: • The field exerts a force on the particle. • The gravitational field is defined as • Gravitational field = Gravitational Force experienced by a “test” particle placed at that point divided by the mass of the test particle. – The presence of the test particle is not necessary for the field to exist • The source particle creates the field

• The gravitational field vectors point in the direction of the acceleration a particle would experience if it were placed in that field. Figure • The magnitude is that of the freefall acceleration, g, at that location. • The gravitational field describes the “effect” that any object has on the empty space around itself in terms of the force that would be present if a second object were somewhere in that space

Sect. 13. 5: Gravitational Potential Energy

• The gravitational force is conservative • Recall Ch. 8 discussion of conservative forces: Only for conservative forces can a potential energy U be defined & Total Mechanical Energy is Conserved for Conservative Forces ONLY. Just as in Ch. 8, define the change in Gravitational Potential Energy associated with a displacement of a mass m is as the negative of the work done by the gravitational force on m during the displacement. That is: F(r) is the Gravitational Force. For a mass m in the Earth’s gravitational field,

• Doing this integral: This gives As always, the reference point where the potential energy is zero is arbitrary. Usually choose it at ri , so (1/ri) 0 and Ui 0. This gives • For example, as a particle moves from point A to B, as in the figure its gravitational potential energy changes by DU =

Notes on Gravitational Potential Energy in the Earth’s Gravity • We’ve chosen the zero for the gravitational potential energy at ri where the gravitational force is also zero. This means that Ui = 0 when ri or that This is valid only for r < RE ≥ RE & NOT for r – That is, it is valid outside the Earth’s surface but NOT inside it! – U is negative because of the choice of Ui

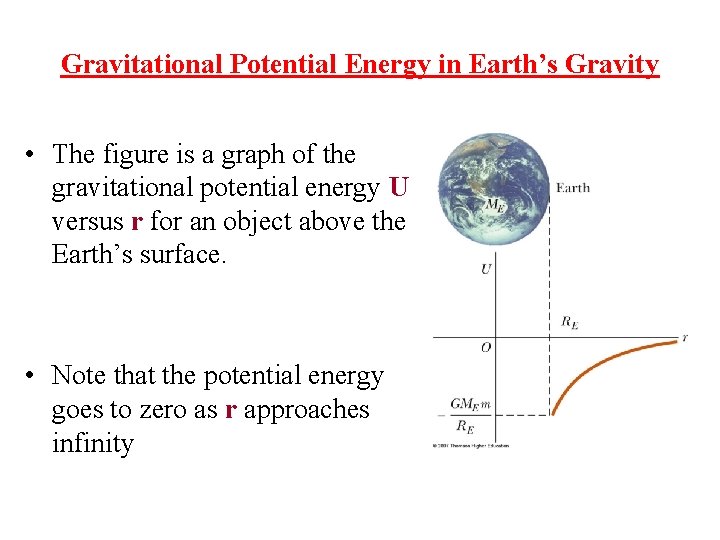
Gravitational Potential Energy in Earth’s Gravity • The figure is a graph of the gravitational potential energy U versus r for an object above the Earth’s surface. • Note that the potential energy goes to zero as r approaches infinity

Gravitational Potential Energy: General Discussion • For any two particles, masses m 1 & m 2, the gravitational potential energy function is • The gravitational potential energy between any two particles varies as 1/r. (Recall that the force varies as 1/r 2) • The potential energy is negative because the force is attractive & we’ve chosen the potential energy to be zero at infinite separation. • Some external energy must be supplied to do the positive work needed to increase the separation between 2 objects – The external work done produces an increase in gravitational potential energy as the particles are separated & U becomes less negative

Binding Energy • The absolute value of the potential energy for mass m can be thought of as the binding energy of m. (The energy of binding of m to the object which is attracting it gravitationally). • Consider two masses m 1 & m 2 attracting each other gravitationally. If an external force is applied to m 1 & m 2 giving them an energy larger than the binding energy, the excess energy will be in the form of kinetic energy of m 1 & m 2 when they are at infinite separation.

Systems with Three or More Particles • For systems with more than two masses, the total gravitational potential energy of the system is the sum of the gravitational potential energy over all pairs of particles. • Because of this, gravitational potential energy is said to obey the superposition principle. Each pair of particles in the system contributes a term to Utotal. • Example; assume 3 particles as in the figure. The result is shown in the equation • The absolute value of Utotal represents the work needed to separate the particles by an infinite distance

Sect. 13. 6: Energy Considerations in Satellite Motion

Energy and Satellite Motion • Consider an object of mass m moving with a speed v in the vicinity of a large mass M – Assume that M >> m as is the case for a small object orbiting a large one. • The total mechanical energy is the sum of the system’s kinetic and potential energies. • Total mechanical energy: E = K +U • In a system in which m is bound in an orbit around M, can show that E must be less than 0

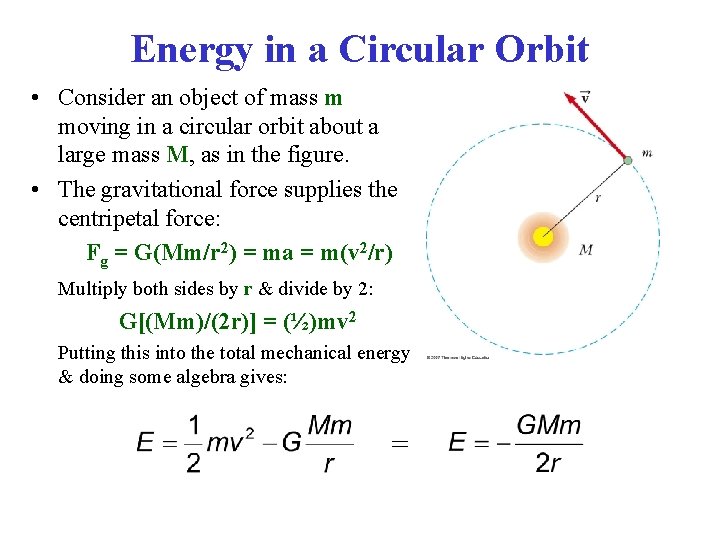
Energy in a Circular Orbit • Consider an object of mass m moving in a circular orbit about a large mass M, as in the figure. • The gravitational force supplies the centripetal force: Fg = G(Mm/r 2) = ma = m(v 2/r) Multiply both sides by r & divide by 2: G[(Mm)/(2 r)] = (½)mv 2 Putting this into the total mechanical energy & doing some algebra gives: =

• The total mechanical energy is negative in for a circular orbit. • The kinetic energy is positive and is equal to half the absolute value of the potential energy • The absolute value of E is equal to the binding energy of the system

Energy in an Elliptical Orbit • It can be shown that, for an elliptical orbit, the radius of the circular orbit is replaced by the semimajor axis, a, of the ellipse. This gives: • The total mechanical energy is negative • The total energy is conserved if the system is isolated

Escape Speed from Earth • Consider an object of mass m projected upward from the Earth’s surface with an initial speed, vi as in the figure. • Use energy to find the minimum value of the initial speed vi needed to allow the object to move infinitely far away from Earth. E is conserved (Ei = Ef), so, to get to a maximum distance away (rmax) & then stop (v = 0): (½)mvi 2 - G[(MEm)/(RE)] = -G[(MEm)/(rmax)] We want vi for rmax the right side is 0 so (½)mvi 2 = G[(MEm)/(RE)]. Solve for vi = vescape This is independent of the direction of vi & of the object mass m!

Escape Speed, General • The result for Earth can be extended to any planet • The table gives escape speeds from various objects. • Note: Complete escape from an object is not really possible – Gravitational force extends to infinity so some force will always be felt no matter how far away you get • This explains why some planets have atmospheres and others do not – Lighter molecules have higher average speeds and are more likely to reach escape speeds