Secret keys and random numbers from quantum non

Secret keys and random numbers from quantum non locality Serge Massar

Message of this talk: Quantum Information uses the weirdness of quantum mechanics to realise tasks impossible classicaly

Message of this talk: Quantum Information uses the weirdness of quantum mechanics to realise tasks impossible classicaly Device Independent approach uses the weirdness of quantum non locality to realise tasks impossible within the usual paradigm of quantum information. Device Independent: • QKD • Certified Random Number Generation • Device Independent quantum state estimation • Self Testing of Quantum Computers

Summary of Talk • Entanglement & Non Locality • Device Independent: – Quantum Key Distribution – Random Number Generator – State Estimation – Self Testing of Quantum Computers • Conclusion
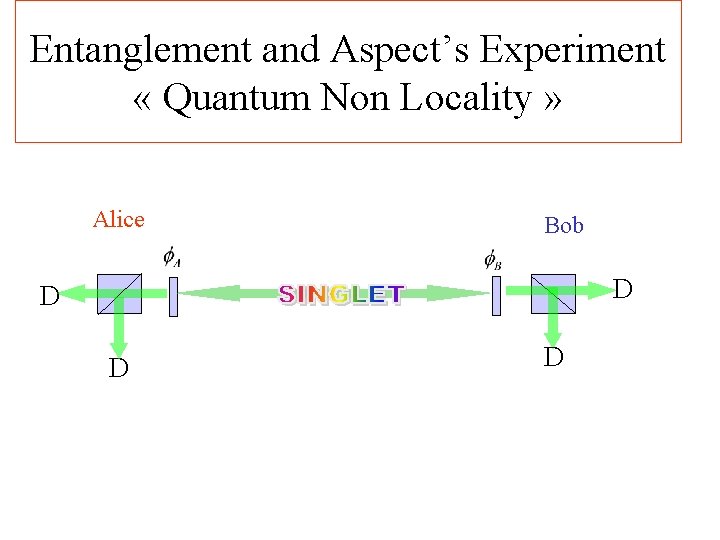
Entanglement and Aspect’s Experiment « Quantum Non Locality » Alice Bob D D
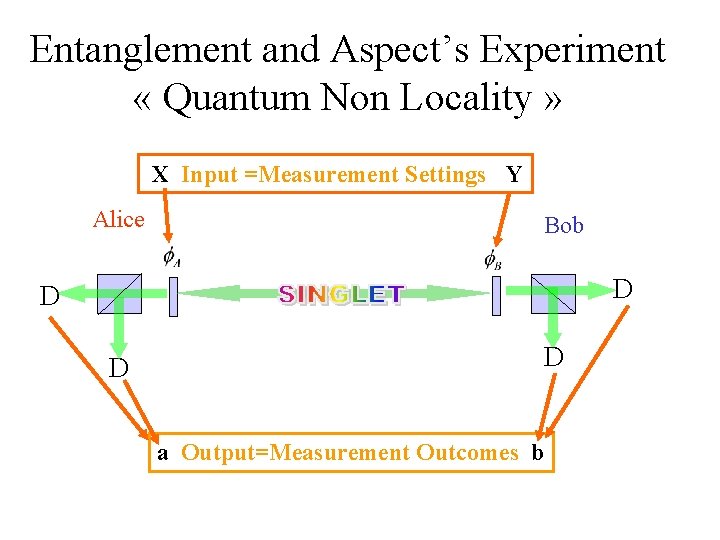
Entanglement and Aspect’s Experiment « Quantum Non Locality » X Input =Measurement Settings Y Alice Bob D D a Output=Measurement Outcomes b
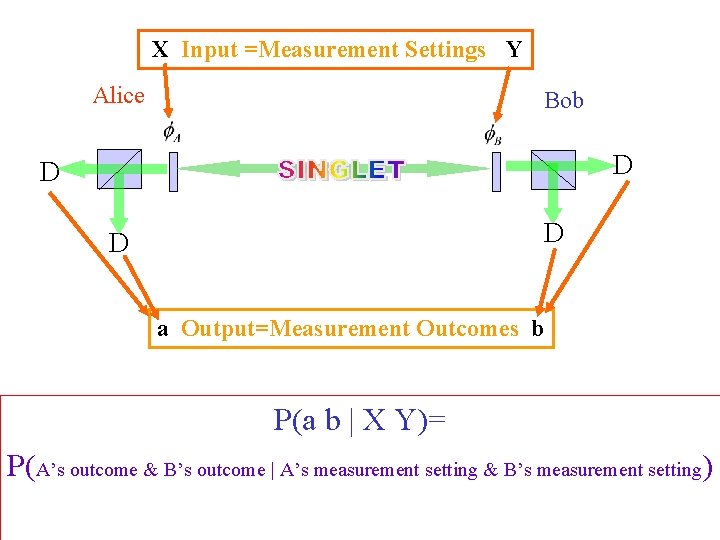
X Input =Measurement Settings Y Alice Bob D D a Output=Measurement Outcomes b P(a b | X Y)= P(A’s outcome & B’s outcome | A’s measurement setting & B’s measurement setting)

P(a b | X Y) Properties of Probabilities: X=Alice’s setting a=Alice’s outcome Y=Bob’s setting b=Bob’s outcome No Signalling Conditions
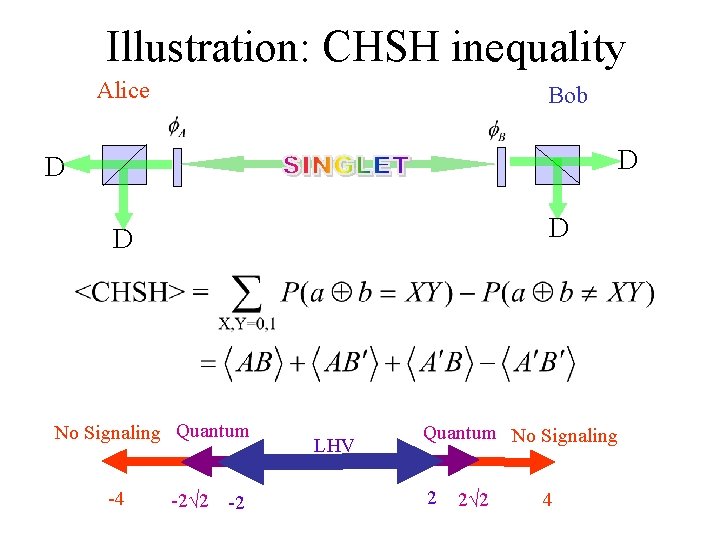
Illustration: CHSH inequality Alice Bob D D No Signaling Quantum -4 -2√ 2 -2 LHV Quantum No Signaling 2 2√ 2 4
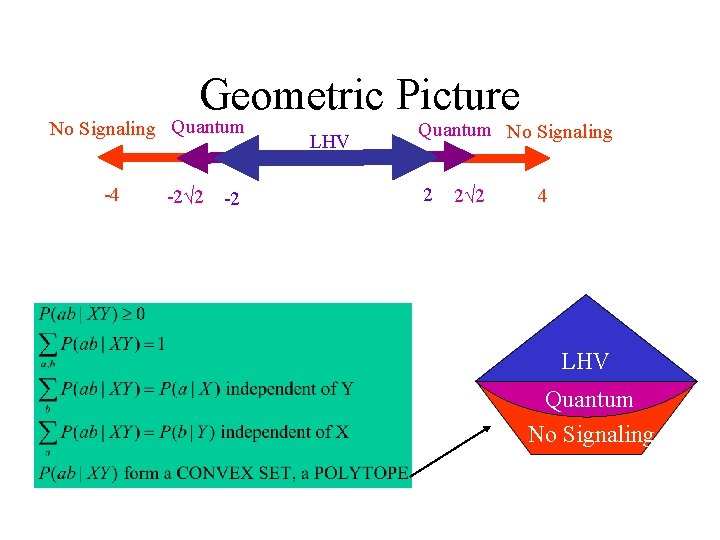
Geometric Picture No Signaling Quantum -4 -2√ 2 -2 LHV Quantum No Signaling 2 2√ 2 4 quantum LHV Quantum No Signaling

4 Interpretations-4 Models Local Hidden Variables • • • Compatible with Determinism Hidden variables determine in advance the results of measurements No Signaling Information cannot travel faster than the speed of light Contradicts Experiments (Except for detection loophole)

4 Interpretations-4 Models Quantum Mechanics • Non Deterministic Outcomes of measurements not defined in advance • No Signaling Information cannot travel faster than the speed of light • Agrees with Observations «Quantum Non Locality»

4 Interpretations-4 Models Non Local Hidden Variables • Compatible with Determinism Hidden variables determine in advance the results of measurements • Non Local The hidden variables are global. Information travels faster than c Contradicts Relativity Exponentially Inefficient • •

4 Interpretations-4 Models Conspiracy Theories • • Everything is Predetermined No Freedom to Choose Measurement Settings No Free Will Contradicts the Locality of Physical Interactions • Exponentially Inefficient ?

Implications for Crypto Local Hidden Variables • • • Compatible with Determinism Hidden variables determine in advance the results of measurements No Signaling Information cannot travel faster than the speed of light Contradicts Experiments (Except for detection loophole) Quantum Mechanics • Non Deterministic Outcomes of measurements not defined in advance • No Signaling Information cannot travel faster than the speed of light • Agrees with Observations «Quantum Non Locality» Non Local Hidden Variables Conspiracy Theories • Compatible with Determinism Hidden variables determine in advance the results of measurements • Non Local The hidden variables are global. Information travels faster than c Contradicts Relativity Exponentially Inefficient ? Contradicts the Locality of Physical Interactions • • Everything is Predetermined No Freedom to Choose Measurement Settings No Free Will • Exponentially Inefficient ?
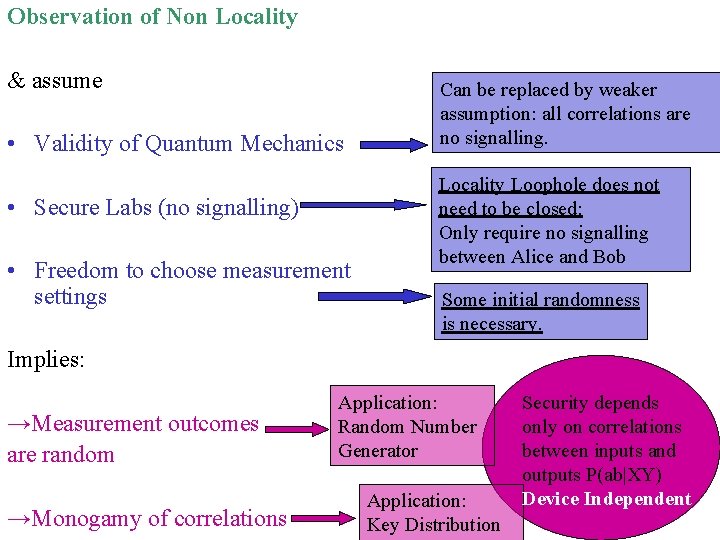
Observation of Non Locality & assume • Validity of Quantum Mechanics • Secure Labs (no signalling) • Freedom to choose measurement settings Can be replaced by weaker assumption: all correlations are no signalling. Locality Loophole does not need to be closed: Only require no signalling between Alice and Bob Some initial randomness is necessary. Implies: →Measurement outcomes are random →Monogamy of correlations Application: Random Number Generator Application: Key Distribution Security depends only on correlations between inputs and outputs P(ab|XY) Device Independent

And the Experimental Situation ? !!!!!!! Rate = m. Hz !!!!!!!!

Quantum Key Distribution What about Security?
Quantum Key Distribution What about Security?

Quantum Key Distribution What about Security?

Quantum Key Distribution What about Security? Practical QKD Beware of the hidden side channel Beware of inefficient detectors Solution: Device Independent Approach

Device Independent QKD • • • Ekert 1991 Mayers and Yao 2004 Barrett Hardy and Kent 2005 Acín Brunner Gisin Massar Pironio and Scarani 2007 M. Mc. Kague, ar. Xiv: 0908. 0503 • Key Idea: Monogamy of Non Local Correlations

Device Independent QKD • Key Idea: Monogamy of Non Local Correlations • Security depends only on the correlations between inputs and outputs • No hypothesis needed – on Hilbert space dimension – on workings of devices • they could even be provided by an adversary

Device Independent QKD To make the concept practical: • Theory needed: security proof when the same devices are used in succession • Experiment needed: Non Locality Experiments with: – detection loophole closed – High data rate – Long Distance Communication • Not necessary to close locality loophole !! – Security of Laboratories is Necessary for crypto – Security of Laboratories Sufficient to enforce No Signalling • Could even be secure against Post-Quantum Adversary – Only require that No Signalling Conditions be Enforced.

Random Number Generators

Random Number Generators Are RNG’s secure? -Are the bits random? (statistical tests only say that they look random) -Are they secret? (maybe the device has failed, is preprogramed)

Device Independent Random Number Generator Kollbeck, Ph. D thesis Pironio Acin Massar Boyer de la Giroday Matsukevich Maunz Olmschenk Hayes Luo Manning Monroe, submitted • Key Ideas: – Monogamy of Non Local Correlations P(abe|XYE)≈P(ab|XY)P(e|E) → adversary has no knowledge of a, b – Violation of a Bell inequality implies that outcomes a, b are random → new random numbers are generated

Device Independent Random Number Generator • Key Idea: – Monogamy of Non Local Correlations P(abe|XYE)≈P(ab|XY)P(e|E) → adversary has no knowledge of a, b – Violation of a Bell inequality implies that outcomes a, b are random → new random numbers are generated Even Secure Against Post Quantum adversary limited only by No-Signalling

Device Independent Random Number Generator • Key Idea: – Monogamy of Non Local Correlations P(abe|XYE)≈P(ab|XY)P(e|E) → adversary has no knowledge of a, b – Violation of a Bell inequality implies that outcomes a, b are random → new random numbers are generated • Randomness Expansion: – Most of the time choose X=Y=0 – From time to time test other settings → Use O(n Log n) random bits to produce O(n 2) new random bits

Experimental Demonstration Theory: takes into account possible memory of devices Use two ions in two traps separated by about 1 m !!Not Necessary to close Locality Loophole!! Detection loophole closed

Experimental Demonstration Theory: takes into account possible memory of devices Use two ions in two traps separated by about 1 m !!Not Necessary to close Locality Loophole!! Detection loophole closed • Number of events n=3016 • Data acquisition time: 1 month • <CHSH>=2. 414 • 42 new private random bits produced at 99% confidence level

Experimental Demonstration Theory: takes into account possible memory of devices Use two ions in two traps separated by about 1 m !!Not Necessary to close Locality Loophole!! Detection loophole closed • Number of events n=3016 • Data acquisition time: 1 month • <CHSH>=2. 414 • 42 new private random bits produced at 99% confidence level For the first time, the randomness of a source can be certified by something more fundamental than statistical tests.
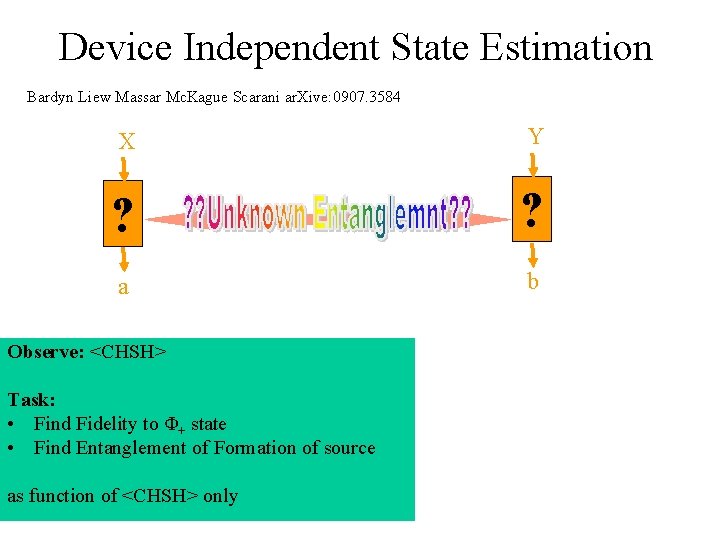
Device Independent State Estimation Bardyn Liew Massar Mc. Kague Scarani ar. Xive: 0907. 3584 X Y ? ? a b Observe: <CHSH> Task: • Find Fidelity to Φ+ state • Find Entanglement of Formation of source as function of <CHSH> only
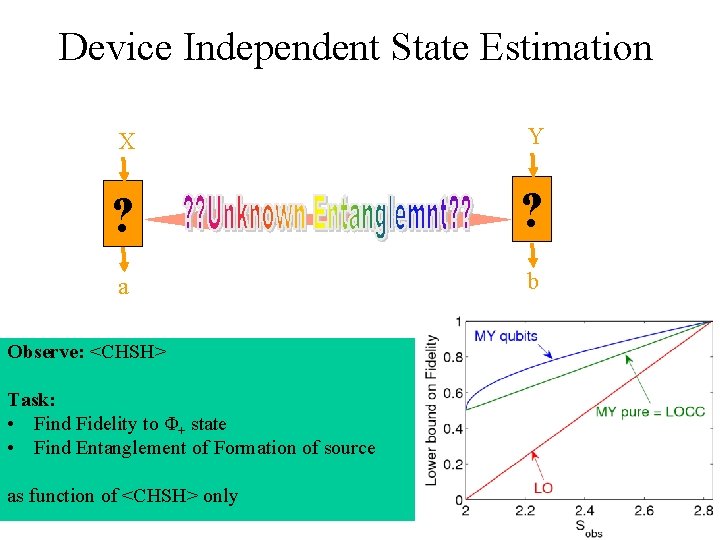
Device Independent State Estimation X Y ? ? a b Observe: <CHSH> Task: • Find Fidelity to Φ+ state • Find Entanglement of Formation of source as function of <CHSH> only

Dimension Witnesses Brunner Pironio Acin Gisin Méthot Scarani 2008 Vertesi Pal ar. Xiv: 0812. 1572 Briet Buhrman Toner ar. Xiv: 0901. 2009 X Y ? ? a b Observe: Violation of Bell inequality Task: • Find Lower Bound on Dimension of Entangled State as function of violation of Bell inequality only

Self Testing of Quantum Computers Mayers Yao 2004 Magniez Mayers Mosca Ollivier 2006 First Quantum Computer ? output Repeatedly measure Second Quantum Computer ? Results of measurements Certify that computer output is correct Repeated Use of Unknown Quantum Computer, using Unknown Entanglement, with intermediate measurements can Certify that output of computation is correct.

Message of this talk: Use the weirdness of quantum non locality to realise tasks impossible within the usual paradigm of quantum information: Device Independent • Quantum Key Distribution • Certified Random Number Generation • Quantum State Estimation • Self Testing of Quantum Computers Overview: A. Ekert, Less Reality, More Security, Physics World, Sept 2009, pp. 28 -32
- Slides: 37