Second Semester2009 CPCS 222 Discrete Structures I Intro

Second Semester/2009 CPCS 222 Discrete Structures I Intro + Sets I. Asmaa & I. Omaima & I. Suha 1

Second semester 2010 Welcome to CPCS 222 n Meet your Instructor. n Course Syllabus available at course group: n http: // n groups. yahoo. com/group/2010 DS_Second Term n Textbook: “Discrete Mathematics and Its Applications”, by Kenneth Rosen, 6 th ed. I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Welcome to CPCS 222 n Important Dates: n 1 st Exam: chapters 1, 2 n 2 nd Exam: chapters 8, 5 n Important Notes: n Absence Policy n Class Behavior I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Why study Discrete Structures n Digital computers are based on discrete “atoms” (bits). n Therefore, both a computer’s n structure (circuits) and n operations (execution of algorithms) n can be described by discrete math. I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Why study Discrete Structures n Uses of Discrete Math in Computer Science n Graphics & animation algorithms, game engines n Advanced algorithms & data structures n Programming language n Compilers & interpreters n Database management systems n Computer networks n Operating systems n Computer architecture n Error correction codes n Software Engineering n Artificial Intelligence n Security & Cryptography I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Basic Structures: Sets & Functions Sets I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Set definition n Set is the fundamental discrete structure on which all other discrete structures are built. n Sets are used to group objects together. Often, the objects in a set have similar properties. n A set is an unordered collection of objects. n The objects in a set are called the elements, or members, of the set I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Some Important Sets The set of natural numbers: N = {0, 1, 2, 3, . . . } The set of integers: Z = {. . . , − 2, − 1, 0, 1, 2, . . . } The set of positive integers: Z+ = {1, 2, 3, . . . } The set of fractions: Q = {0, ½, – 5, 78/13, …} Q ={p/q | pЄ Z , qЄZ, and q≠ 0 } The set of Real: R = {– 3/2, 0, e, π2, sqrt(5), …} I. Asmaa & I. Omaima & I. Suha 8

Second semester 2010 Notation used to describe membership in sets n a set A is a collection of elements. n If x is an element of A, we write x A; If not: x A. n x A Say: “x is a member of A” or “x is in A”. n Note: Lowercase letters are used for elements, capitals for sets. n Two sets are equal if and only if they have the same elements A= B : x( x A x B) I. Asmaa & I. Omaima & I. Suha 9

Second semester 2010 How to describe a set? n List all the members of a set, when this is possible. We use a notation where all members of the set are listed between braces. { } Example : {dog, cat, horse} n Sometimes the brace notation is used to describe a set without listing all its members. Some members of the set are listed, and then ellipses (. . . ) are used when the general pattern of the elements is obvious. Example: The set of positive integers less than 100 can be denoted by {1, 2, 3, . . . , 99}. I. Asmaa & I. Omaima & I. Suha

Second semester 2010 How to describe a set? n Another way to describe a set is to use set builder notation. We characterize all those elements in the set by stating the property or properties they must have to be members. n Example: the set O of all odd positive integers less than 10 can be written as: O = {x | x is an odd positive integer <10} or, specifying the universe as the set of positive integers, as O = {x Z+ | x is odd and x<10}. I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Sets The Empty Set (Null Set) We use to denote the empty set, i. e. the set with no elements. For example: the set of all positive integers that are greater than their squares is the null set. Singleton set A set with one element is called a singleton set. I. Asmaa & I. Omaima & I. Suha 12

Second semester 2010 Sets n Computer Science n Note that the concept of a datatype, or type, in computer science is built upon the concept of a set. In particular, a datatype is the name of a set, together with a set of operations that can be performed on objects from that set. n For example, Boolean is the name of the set {0, 1} together with operators on one or more elements of this set, such as AND, OR, and NOT. I. Asmaa & I. Omaima & I. Suha

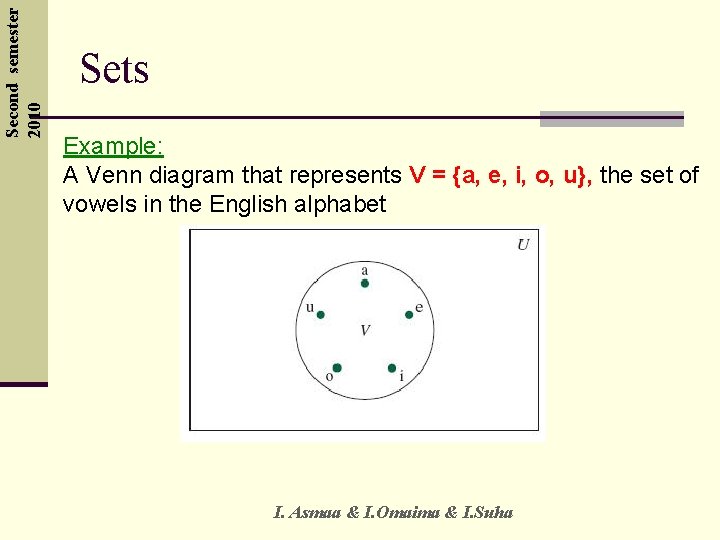
Second semester 2010 Sets Venn diagrams q Sets can be represented graphically using Venn diagrams. q In Venn diagrams the universal set U, which contains all the objects under consideration, is represented by a rectangle. q Inside this rectangle, circles or other geometrical figures are used to represent sets. q Sometimes points are used to represent the particular elements of the set. I. Asmaa & I. Omaima & I. Suha 14

Second semester 2010 Sets Example: A Venn diagram that represents V = {a, e, i, o, u}, the set of vowels in the English alphabet I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Subset q The set A is said to be a subset of B if and only if every element of A is also an element of B. q We use the notation A B to indicate that A is a subset of the set B. q We see that A B if and only if the quantification x (x A → x B) is true. I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Finite and Infinite Sets Finite set q Let S be a set. If there are exactly n distinct elements in S where n is a nonnegative integer, we say that S is a finite set and that n is the cardinality of S. q The cardinality of S is denoted by |S|. Infinite set A set is said to be infinite if it is not finite. For example, the set of positive integers is infinite. 17 I. Asmaa & I. Omaima & I. Suha

Second semester 2010 The power of a set q Many problems involve testing all combinations of elements of a set to see if they satisfy some property. q To consider all such combinations of elements of a set S, we build a new set that has as its members all the subsets of S. q Given a set S, the power set of S is the set of all subsets of the set S. The power set of S is denoted by P(S). q if a set has n elements , then the power has 2 n elements I. Asmaa & I. Omaima & I. Suha 18

Second semester 2010 The power of a set Example: What is the power set of the set {0, 1, 2}? P({0, 1, 2}) is the set of all subsets of {0, 1, 2} P({0, 1, 2})= { , {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}} What is the power set of the empty set? What is the power set of the set { } P( )= { } P({ })= { , { }} 19 I. Asmaa & I. Omaima & I. Suha

Second semester 2010 Cartesian Products q The order of elements in a collection is often important. q Because sets are unordered, a different structure is needed to represent ordered collections. q This is provided by ordered n-tuples. q The ordered n-tuple (a 1, a 2, . . . , an) is the ordered collection that has a 1 as its first element, a 2 as its second element, . . . , and an as its nth element. I. Asmaa & I. Omaima & I. Suha 20

Second semester 2010 Cartesian Products q Let A and B be sets. The Cartesian product of A and B, denoted by A×B, is the set of all ordered pairs (a, b), where a A and b B. A×B = {(a, b) | a A b B}. A 1×A 2×…×An= {(a 1, a 2, …, an) | ai Ai for i=1, 2, …, n}. q A×B not equal to B×A Example: What is the Cartesian product A × B × C, where A = {0, 1}, B = {1, 2}, and C = {0, 1, 2}? I. Asmaa & I. Omaima & I. Suha 21

Second semester 2010 For You!! n Exercises: n Page#119: n 1(a, d). n 2(b, c) n 4 n Page#120: n 8(e, d, g) n 10 n 17(d) n 18(c) n 24 n 28 I. Asmaa & I. Omaima & I. Suha