Second Level Multiplication Building on what they learn

Second Level - Multiplication Building on what they learn at First Level • multiplication is commutative, i. e. 2 × 8 = 8 × 2 • multiplication and division are inverses of each other, • i. e. knowing. 2 × 8 = 16 leads to 16 ÷ 8 = 2 and 16 ÷ 2 = 8 many of the tables belong to the same family (e. g. 2, 4 and 8; 3, 6 and 9; 5 and 10) and by understanding how they are related to each other we can work out facts we may not be able to recall. • multiplying by powers of ten is an essential numeracy process. • These activities also use multiples of 10 and 100 to derive new facts from known table facts, e. g. 3 × 4 = 12, so 30 × 4 = 120 and 300 × 4 = 1, 200

Arrays • This array shows 7 rows of 8 dots which can be written as 7 × 8 = 56. Rotate it by a quarter turn and it shows 8 × 7 = 56, i. e. multiplication is commutative. • • • • • • • • • • • • • •

Arrays 7 • • • • • • • • • • • • • • • • X 16 • • • • • • • • • • • • • It shows 7 rows of 16. How does this help us figure out the answer? Partition it into manageable sums.

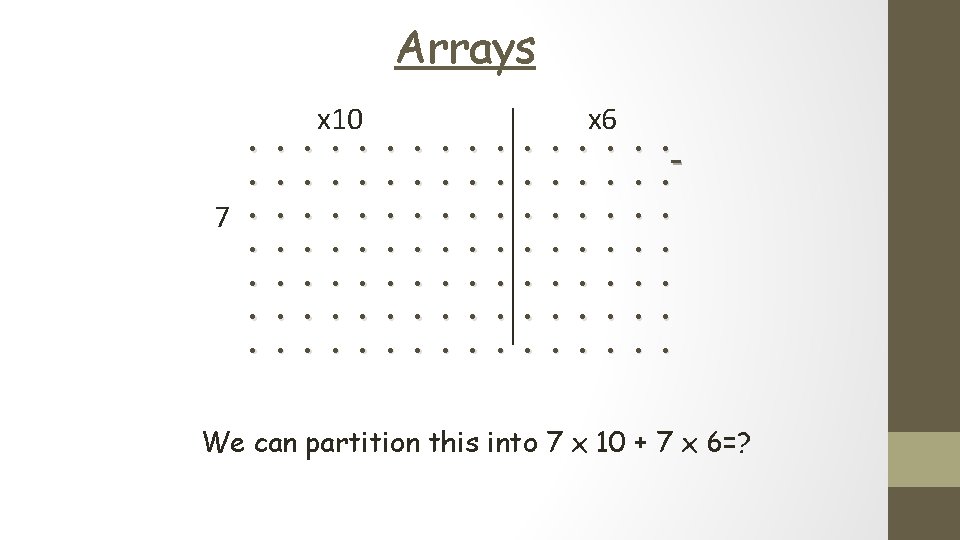
Brackets • This would be shown as (7 x 10) + 70 (7 x 6)= + 42 = 112 • Brackets are used to show the thinking behind the partitioning and children should be becoming increasingly confident with their use, understanding that the calculation within has to be done before any other combining.

Brackets • As multiplication is commutative, 2 × 7 × 5 is the same as 2 × 5 × 7. It is easier to swap the numbers round to make a calculation of (2 × 5) × 7 because we know that 2 × 5 makes 10 • We would look for a rounded number when we are using brackets and moving 3 or more multiplications around to help us. • Similarly we do the same with our arrays.

Arrays • We extend the use of arrays by dropping the dots within them and concentrating on the rectangles that can be partitioned into manageable sums. These look to use the example of the earlier arrays, and partitioning, to make multiplying a single digit by 2, 3 and more digits X 26 7

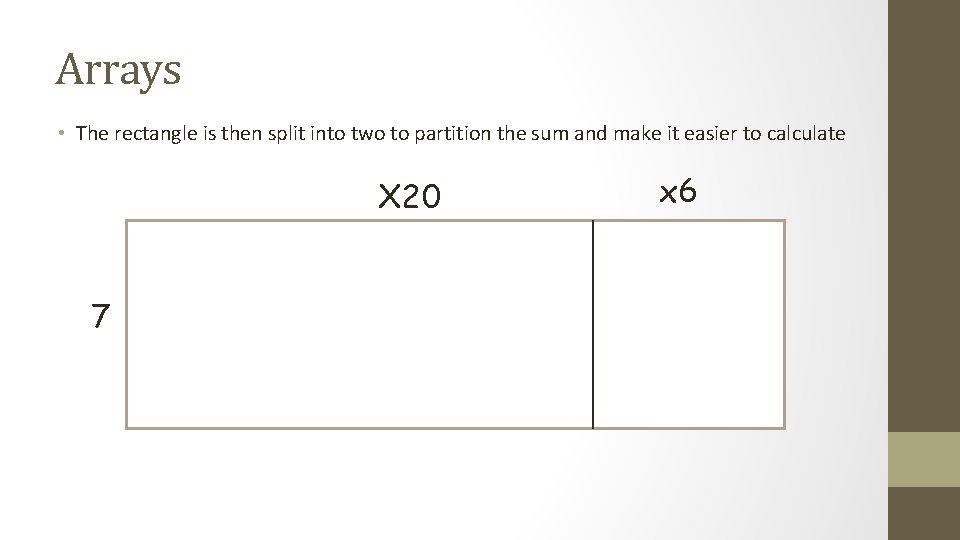
Arrays • The rectangle is then split into two to partition the sum and make it easier to calculate X 20 7 x 6

We then use Brackets to complete the sum (7 x 20) + (7 x 6) = 140 + 42 = 182 It then leads on towards the formal method. 26 x 7 140 42 182 (7 x 20) (7 x 6)

Division How we now approach long division calculations

What is division The action of separating something into parts. Introduced through the idea of sharing 18 sweets into 6 bags. What if the problem becomes 18 sweets to be shared amongst 6 bags? Repeated subtraction.

Long Division Our memories of long division? Why do most not have positive memories of the processes Only those who had confidence in all number would be successful in answering any long division questions. Endless pages of practice of the process to get the answer No need to understand the maths, just reliance on the written operations

Why change? We all carry a calculator in our pocket. Still require strong number skills to make sense of every day numbers Mobile phone sales people Politician statistics ……. .

So Chunking? Repeated subtraction Easier to link between multiplication and division More like the everyday mental process of division Does not rely as much on abilities to memorise all times tables and facts. Although sound tables awareness does make the whole process easier

Chunking 96÷ 6 92÷ 4 2 digit by 1 digit 153÷ 9 154÷ 7 3 digit by 1 digit 396÷ 12 540÷ 15 3 digits by 2 digits

Would you like a try? Text book examples ( pages 59 -65) Number Investigations Presenting to each other Games, Fact files, information/guide books Word problems in different context requiring choice of operation (textboog page 74 on) Setting partner challenges (Similar to the ones set above)