Secants Tangents and Angle Measures Find measures of

Secants, Tangents and Angle Measures • Find measures of angles formed by lines intersecting on or inside a circle. • Find measures of angles formed by lines intersecting outside the circle. Water droplet on a CD

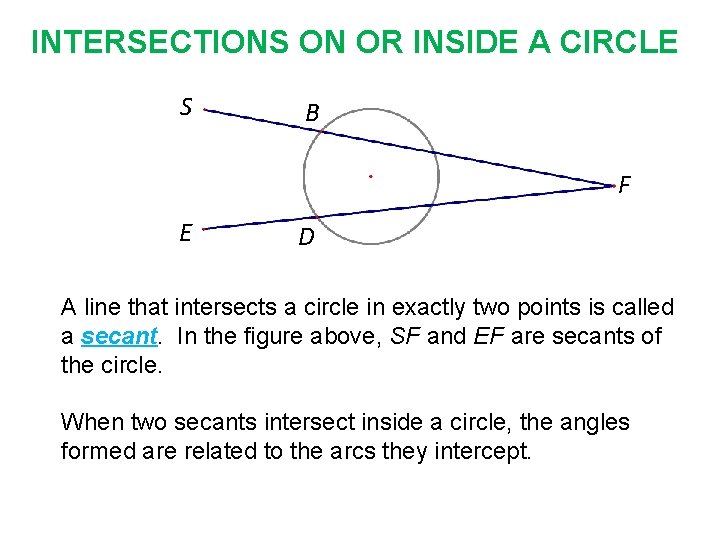
INTERSECTIONS ON OR INSIDE A CIRCLE S B F E D A line that intersects a circle in exactly two points is called a secant. In the figure above, SF and EF are secants of the circle. When two secants intersect inside a circle, the angles formed are related to the arcs they intercept.

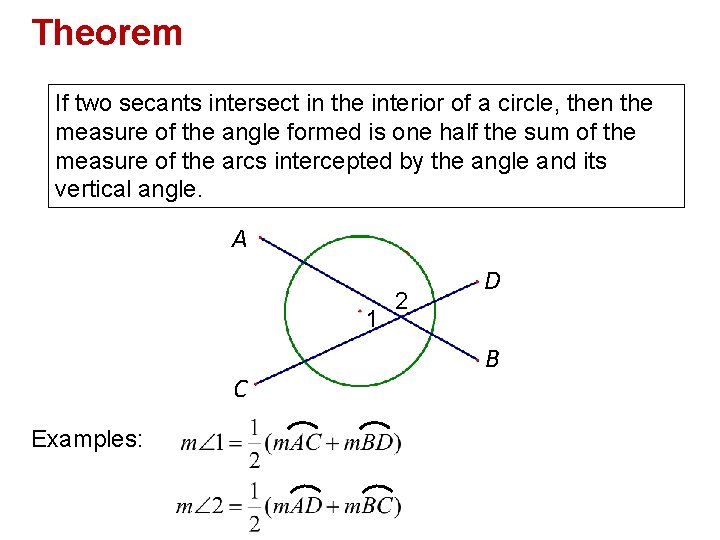
Theorem If two secants intersect in the interior of a circle, then the measure of the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle. A 1 C Examples: 2 D B

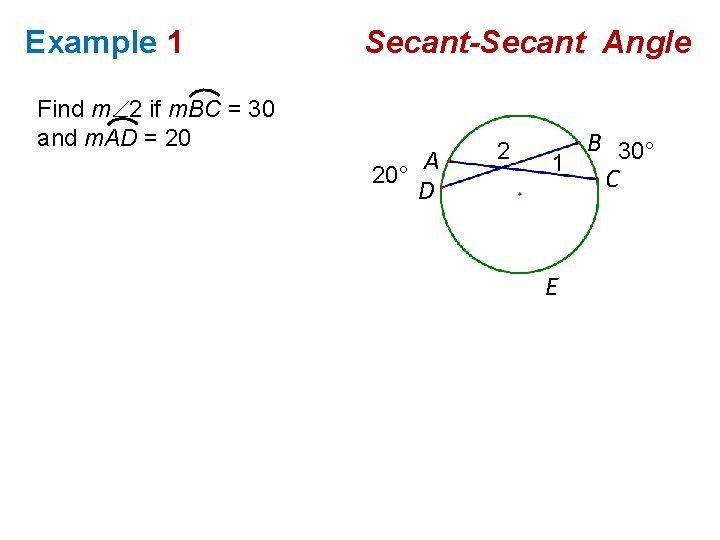
Example 1 Secant-Secant Angle Find m 2 if m. BC = 30 and m. AD = 20 20° A D 2 B 30° 1 C E

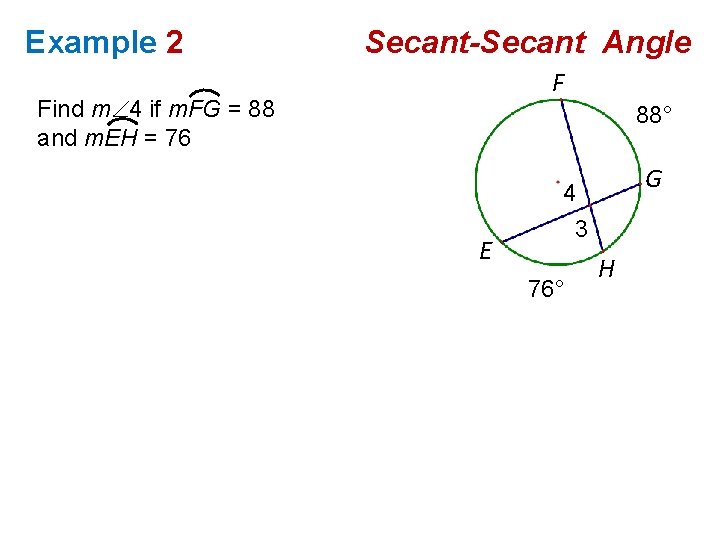
Example 2 Secant-Secant Angle F Find m 4 if m. FG = 88 and m. EH = 76 88° E G 4 3 76° H

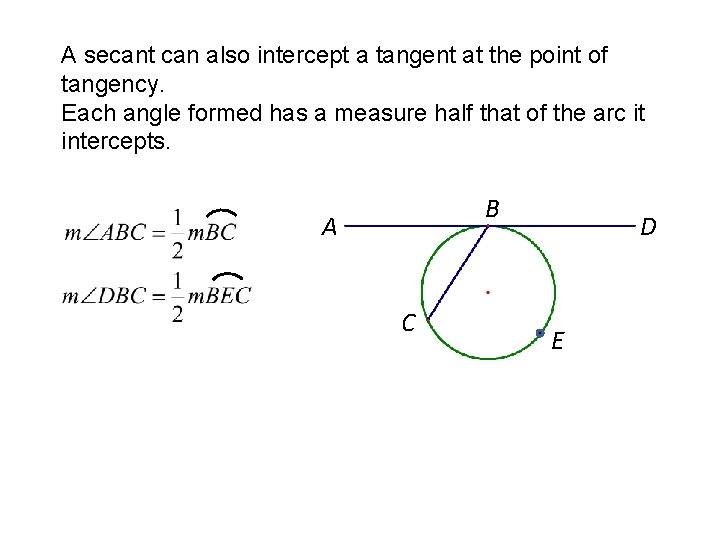
A secant can also intercept a tangent at the point of tangency. Each angle formed has a measure half that of the arc it intercepts. B A C D E

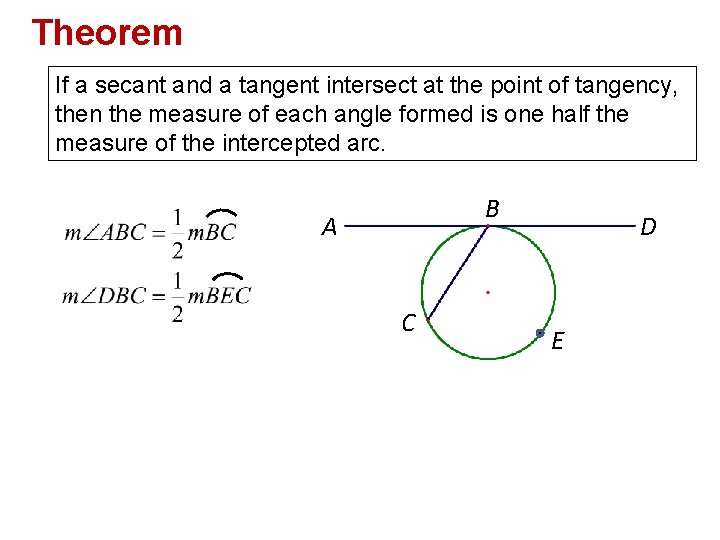
Theorem If a secant and a tangent intersect at the point of tangency, then the measure of each angle formed is one half the measure of the intercepted arc. B A C D E

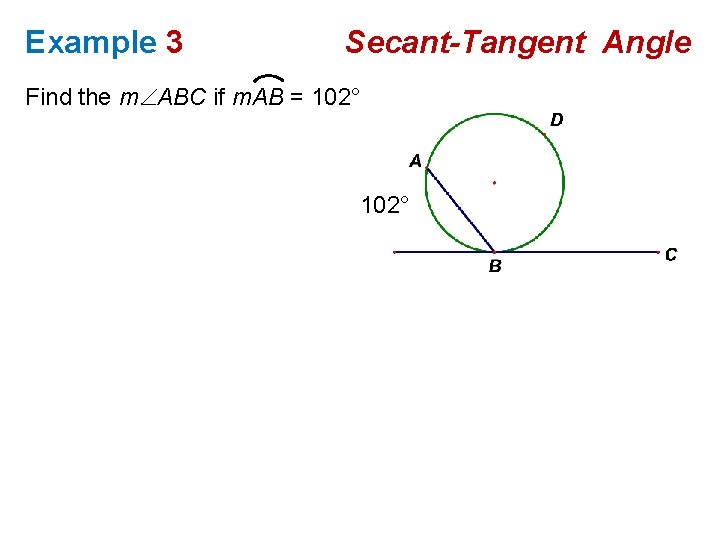
Example 3 Secant-Tangent Angle Find the m ABC if m. AB = 102°

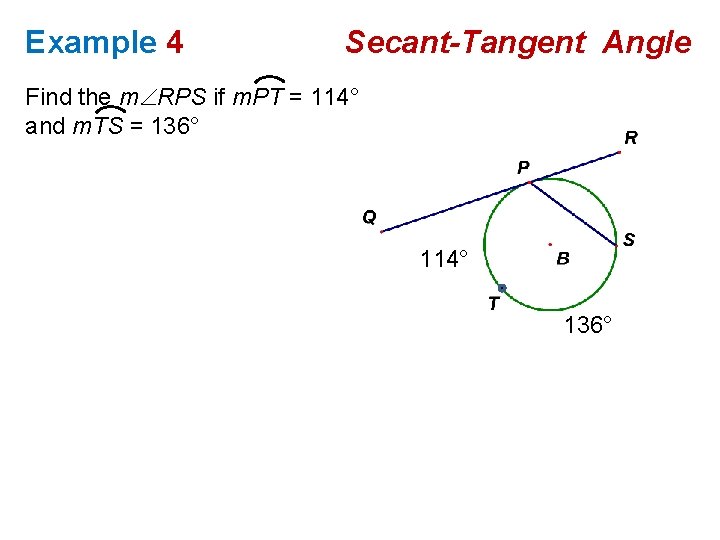
Example 4 Secant-Tangent Angle Find the m RPS if m. PT = 114° and m. TS = 136° 114° 136°

INTERSECTIONS OUTSIDE A CIRCLE Secants and tangents can also intersect outside a circle. The measure of the angle formed also involves half the measure of the arcs they intercept.

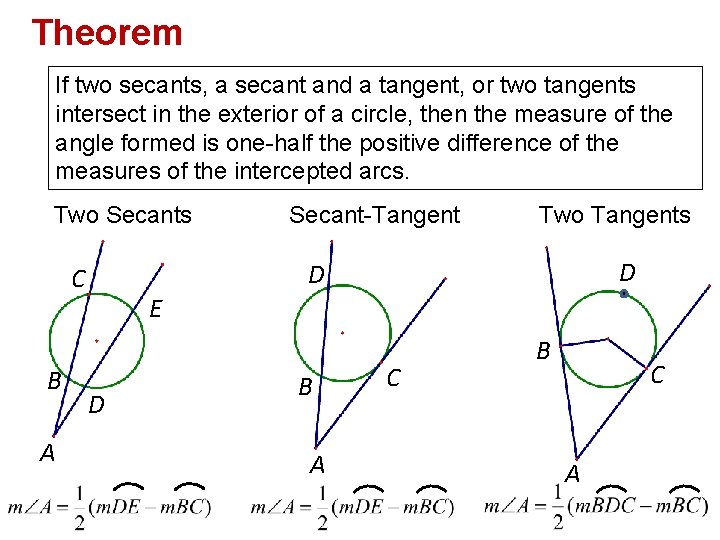
Theorem If two secants, a secant and a tangent, or two tangents intersect in the exterior of a circle, then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs. Two Secants A Two Tangents D D C B Secant-Tangent E D B A C B C A

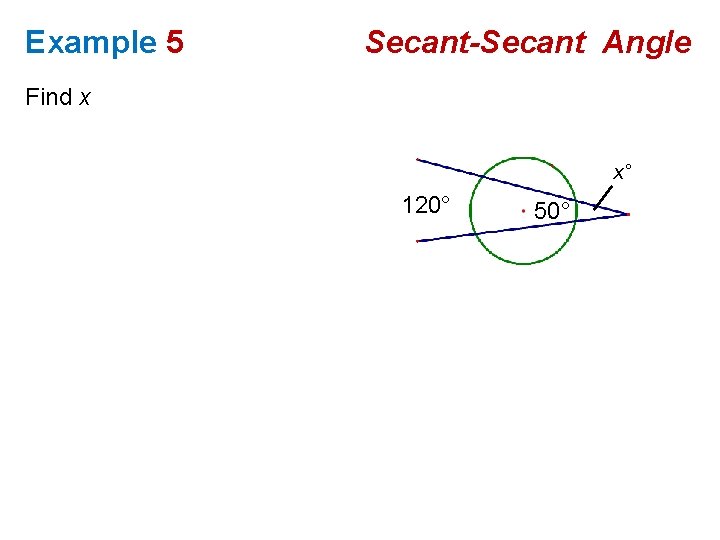
Example 5 Secant-Secant Angle Find x x° 120° 50°

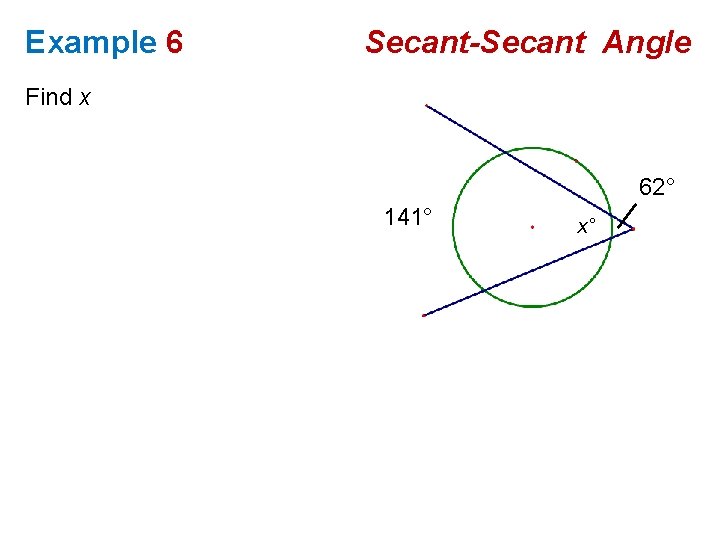
Example 6 Secant-Secant Angle Find x 62° 141° x°

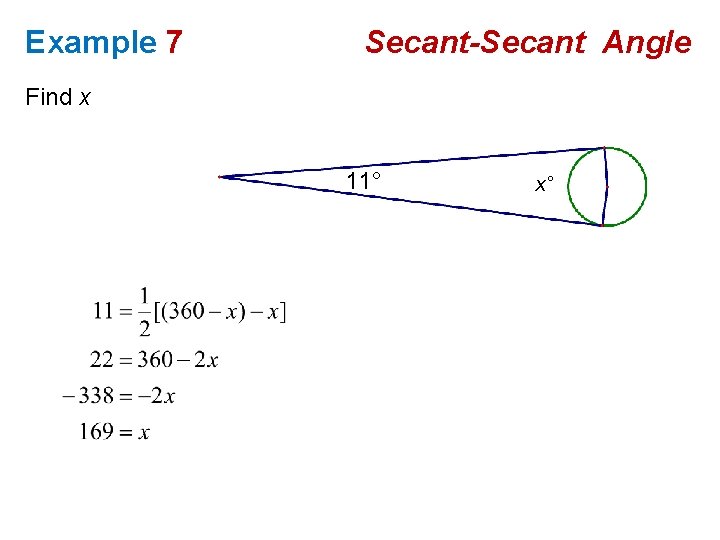
Example 7 Secant-Secant Angle Find x 11° x°