Secant Method Civil Engineering Majors Authors Autar Kaw

Secant Method Civil Engineering Majors Authors: Autar Kaw, Jai Paul http: //numericalmethods. eng. usf. edu Transforming Numerical Methods Education for STEM Undergraduates 3/4/2021 http: //numericalmethods. eng. usf. edu 1

Secant Method http: //numericalmethods. eng. usf. edu

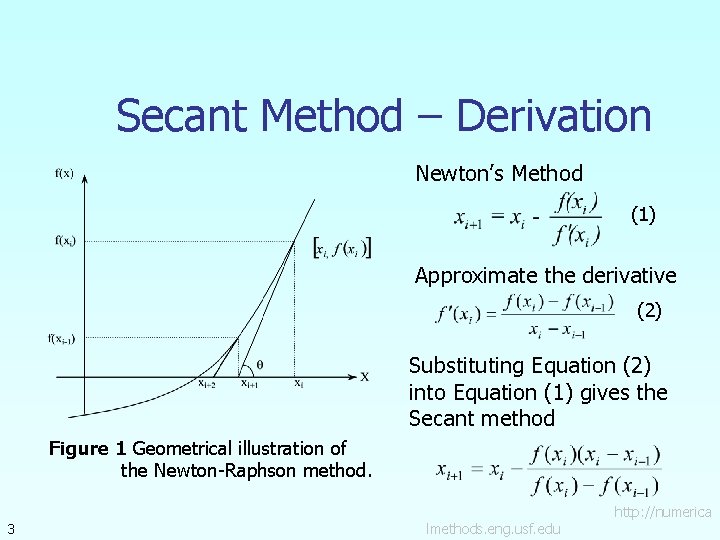
Secant Method – Derivation Newton’s Method (1) Approximate the derivative (2) Substituting Equation (2) into Equation (1) gives the Secant method Figure 1 Geometrical illustration of the Newton-Raphson method. 3 lmethods. eng. usf. edu http: //numerica

Secant Method – Derivation The secant method can also be derived from geometry: The Geometric Similar Triangles can be written as On rearranging, the secant method is given as Figure 2 Geometrical representation of the Secant method. 4 lmethods. eng. usf. edu http: //numerica

Algorithm for Secant Method 5 lmethods. eng. usf. edu http: //numerica

Step 1 Calculate the next estimate of the root from two initial guesses Find the absolute relative approximate error 6 lmethods. eng. usf. edu http: //numerica

Step 2 Find if the absolute relative approximate error is greater than the prespecified relative error tolerance. If so, go back to step 1, else stop the algorithm. Also check if the number of iterations has exceeded the maximum number of iterations. 7 lmethods. eng. usf. edu http: //numerica

Example 1 You are making a bookshelf to carry books that range from 8 ½ ” to 11” in height and would take 29”of space along length. The material is wood having Young’s Modulus 3. 667 Msi, thickness 3/8 ” and width 12”. You want to find the maximum vertical deflection of the bookshelf. The vertical deflection of the shelf is given by where x is the position where the deflection is maximum. Hence to find the maximum deflection we need to find where conduct the second derivative test. 8 lmethods. eng. usf. edu and http: //numerica

Example 1 Cont. The equation that gives the position x where the deflection is maximum is given by Figure 2 A loaded bookshelf. 9 Use the secant method of finding roots of equations to find the position where the deflection is maximum. Conduct three iterations to estimate the root of the above equation. Find the absolute relative approximate error at the end of each iteration and the number of significant digits at least correct at the end of each http: //numerica iteration. lmethods. eng. usf. edu

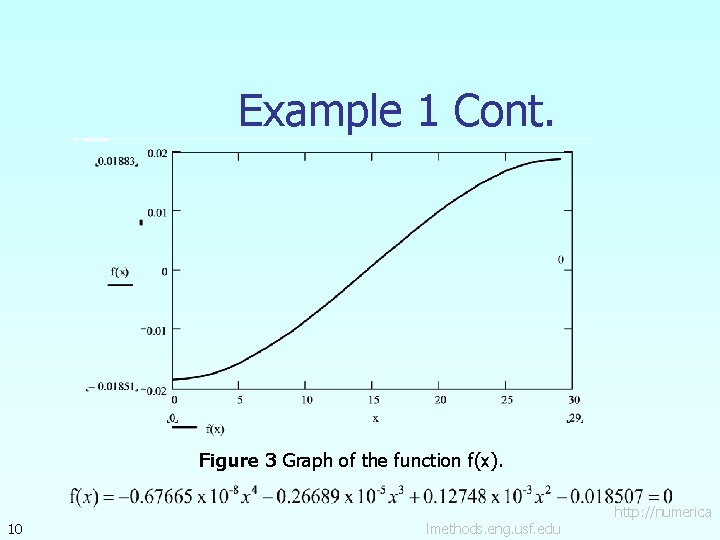
Example 1 Cont. Figure 3 Graph of the function f(x). 10 lmethods. eng. usf. edu http: //numerica

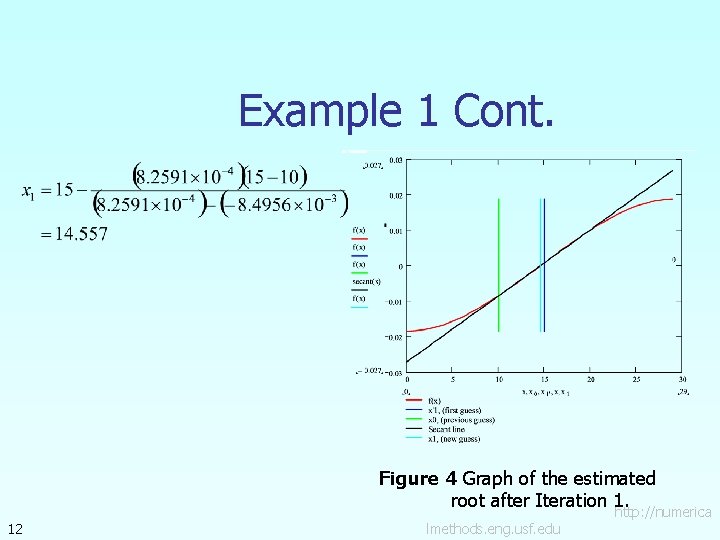
Example 1 Cont. Solution Let us take the initial guesses of the root of Iteration 1 The estimate of the root is 11 as lmethods. eng. usf. edu and . http: //numerica

Example 1 Cont. 12 Figure 4 Graph of the estimated root after Iteration 1. http: //numerica lmethods. eng. usf. edu

Example 1 Cont. The absolute relative approximate error at the end of Iteration 1 is The number of significant digits at least correct is 1, because the absolute relative approximate error is less than 5%. 13 lmethods. eng. usf. edu http: //numerica

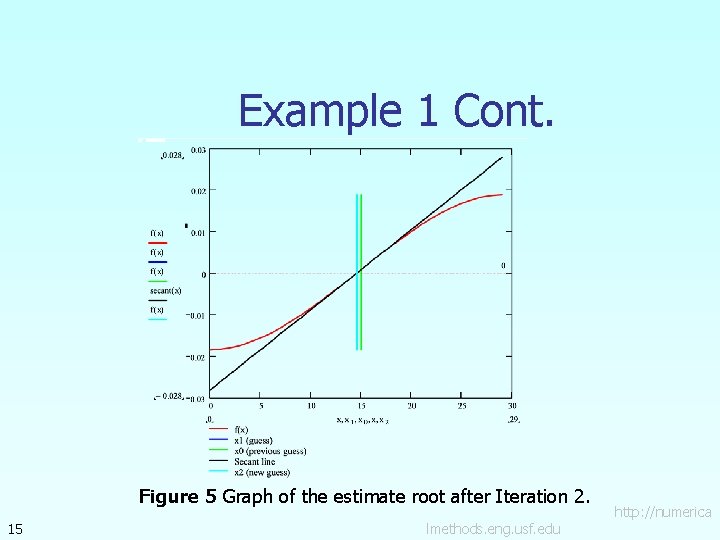
Example 1 Cont. Iteration 2 The estimate of the root is 14 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. Figure 5 Graph of the estimate root after Iteration 2. 15 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. The absolute relative approximate error at the end of Iteration 2 is The number of significant digits at least correct is 2, because the absolute relative approximate error is less than 0. 5%. 16 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. Iteration 3 The estimate of the root is 17 lmethods. eng. usf. edu http: //numerica

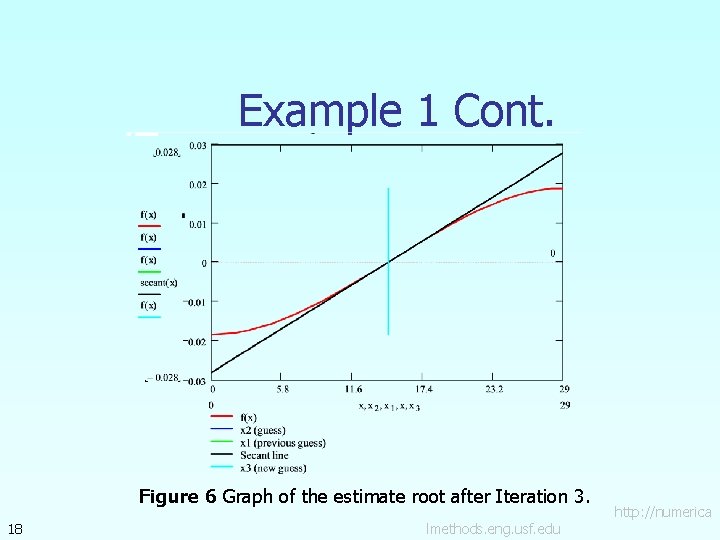
Example 1 Cont. Figure 6 Graph of the estimate root after Iteration 3. 18 lmethods. eng. usf. edu http: //numerica

Example 1 Cont. The absolute relative approximate error at the end of Iteration 3 is The number of significant digits at least correct is 6, because the absolute relative approximate error is less than 0. 00005%. 19 lmethods. eng. usf. edu http: //numerica

Advantages n n 20 Converges fast, if it converges Requires two guesses that do not need to bracket the root lmethods. eng. usf. edu http: //numerica

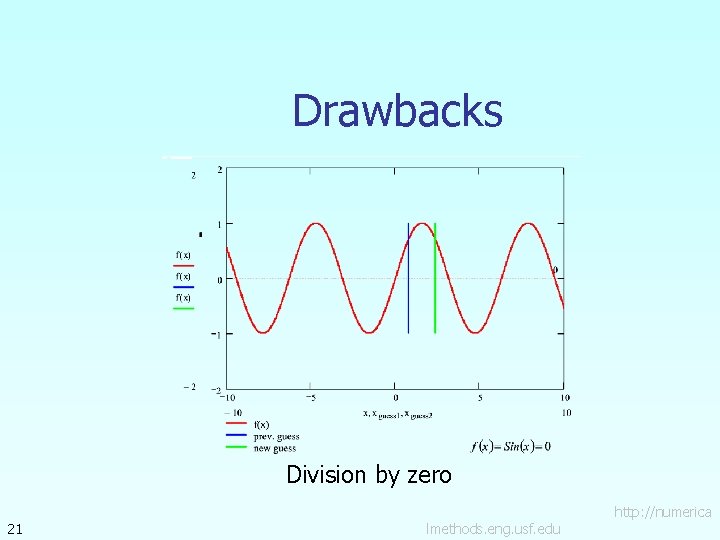
Drawbacks Division by zero 21 lmethods. eng. usf. edu http: //numerica

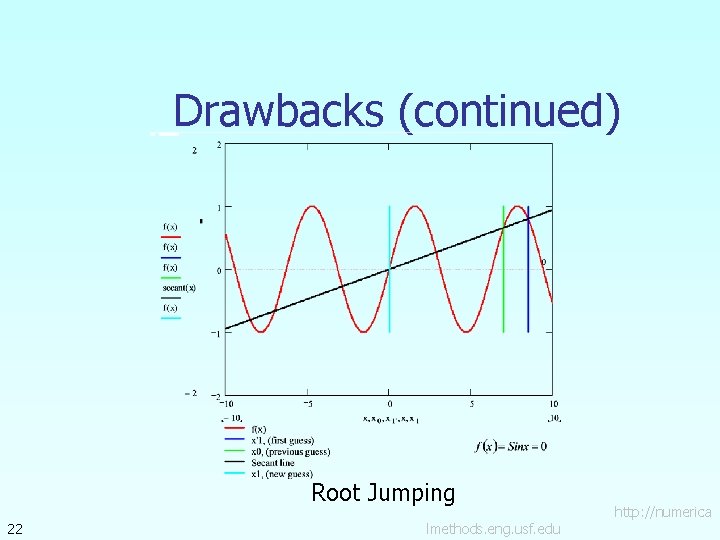
Drawbacks (continued) Root Jumping 22 lmethods. eng. usf. edu http: //numerica

Additional Resources For all resources on this topic such as digital audiovisual lectures, primers, textbook chapters, multiple-choice tests, worksheets in MATLAB, MATHEMATICA, Math. Cad and MAPLE, blogs, related physical problems, please visit http: //numericalmethods. eng. usf. edu/topics/secant_me thod. html

THE END http: //numericalmethods. eng. usf. edu