Sec 7 3 The Jacobi and Gauss Siedel

Sec: 7. 3 The Jacobi and Gauss. Siedel Iterative Techniques

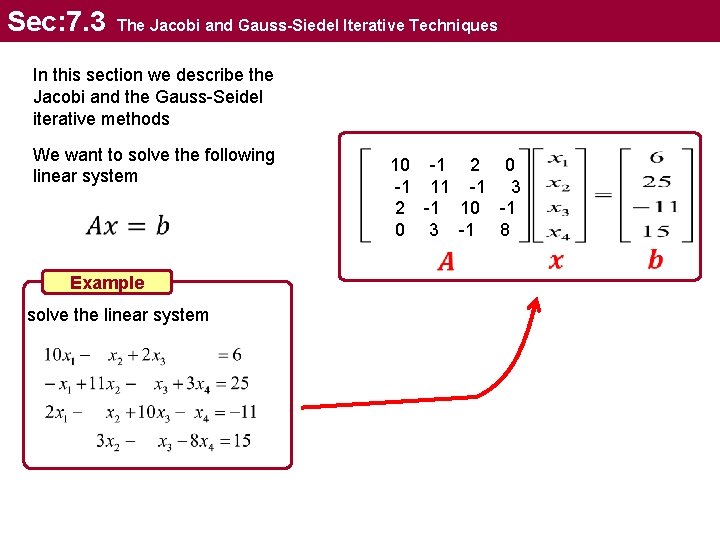
Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques In this section we describe the Jacobi and the Gauss-Seidel iterative methods We want to solve the following linear system Example solve the linear system 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques We want to solve the following linear system Example solve the linear system Keep the diagonal on the left hand side Jacobi Iterative Method Change the coeff of LHS to be one by division

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi Iterative Method

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi Iterative Method 0. 6000 1. 0473 0. 9326 1. 0152 0. 9890 2. 2727 1. 7159 2. 0533 1. 9537 2. 0114 -1. 1000 -0. 8052 -1. 0493 -0. 9681 -1. 0103 1. 8750 0. 8852 1. 1309 0. 9738 1. 0214 1. 0032 0. 9981 1. 0006 0. 9997 1. 0001 1. 9922 2. 0023 1. 9987 2. 0004 1. 9998 -0. 9945 -1. 0020 -0. 9990 -1. 0004 -0. 9998 0. 9944 1. 0036 0. 9989 1. 0006 0. 9998

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi iteration for general n:

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Gauss Seidel Method

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Gauss Seidel Method Note that in the Jacobi iteration one does not use the most recently available information. 0. 6000 1. 0302 1. 0066 2. 3273 2. 0369 2. 0036 -0. 9873 -1. 0145 -1. 0025 0. 8789 0. 9843 0. 9984 1. 0009 2. 0003 -1. 0003 0. 9998 1. 0001 2. 0000 -1. 0000 Note that Jacobi’s method in this example required twice as many iterations for the same accuracy.

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi iteration for general n: Gauss-Seidel iteration for general n:

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques General Iteration Methods

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques General Iteration Methods Splittings and Convergence Example DEF: Splitting A large family of iteration where

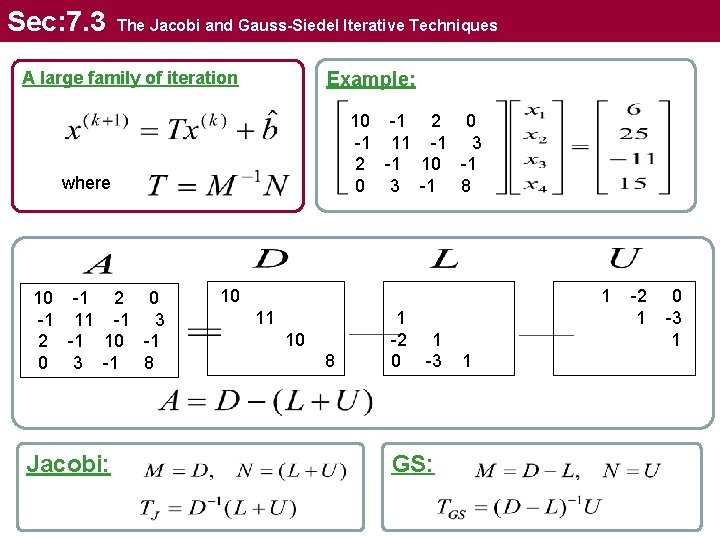
Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Example: A large family of iteration 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 where 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 Jacobi: 10 1 11 10 8 1 -2 0 1 -3 GS: 1 -2 1 0 -3 1

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques We want to solve the following linear system Example solve the linear system Keep the diagonal on the left hand side Change the coeff of LHS to be one by division Jacobi Iterative Method

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Jacobi: GS: A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8]; b = [6; 25; -11; 15]; U=-triu(A, 1); L=-tril(A, -1); D=diag(diag(A)); TJ= D(L+U); b. J = Db; Tgs=(D-L)U; bg = (D-L)b; x=[0; 0; 0; 0]; for i=1: 10 x = TJ*x + b. J; end x x=[0; 0; 0; 0]; for i=1: 5 x = Tgs*x + bg; end x

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques GS: Jacobi: A large family of iteration THM: All eigenvalues of T in absolute value are less than one. where DEF: be nxn matrix with eigenvalues spectral radius of T is defined to be Example

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques A large family of iteration THM: where

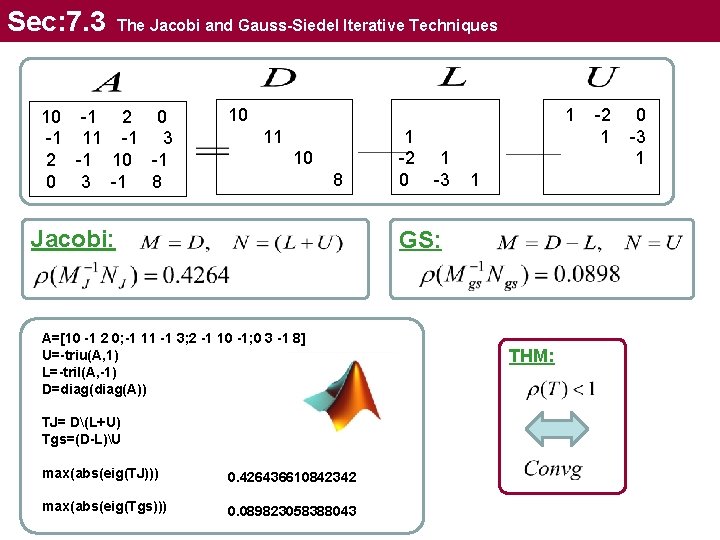
Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 10 1 11 10 8 Jacobi: 1 -2 0 1 -3 1 GS: A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8] U=-triu(A, 1) L=-tril(A, -1) D=diag(A)) TJ= D(L+U) Tgs=(D-L)U max(abs(eig(TJ))) 0. 426436610842342 max(abs(eig(Tgs))) 0. 089823058388043 THM: -2 1 0 -3 1

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Convergence Criterion for the Gauss-Seidel Method A large family of iteration THM: where We can now give easily verified sufficiency conditions for convergence of the Gauss-Seidel methods. Definition A is strictly diagonally dominant That is, the diagonal coefficient in each of the equations must be larger than the sum of the absolute values of the other coefficients in the equation

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Convergence Criterion for the Gauss-Seidel Method Definition A is strictly diagonally dominant Example 1 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 THM: A is strictly diagonally dominant That is, the diagonal coefficient in each of the equations must be larger than the sum of the absolute values of the other coefficients in the equation Example 2 10 -1 2 0 -1 4 -1 3 2 -1 4 -1 0 3 -1 2

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques Definition Example 1 norm of the vector x = (x 1, x 2, x 3)t gives the length of the straight line joining the points (0, 0, 0) and (x 1, x 2, x 3). the distance between two vectors is defined as the norm of the difference of the vectors

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8]; b = [6; 25; -11; 15]; U=-triu(A, 1); L=-tril(A, -1); D=diag(A)); Tgs=(D-L)U; bg = (D-L)b; x=[0; 0; 0; 0]; for i=1: 5 x = Tgs*x + bg; end x Stopping Criteria: residual Example: 10 -1 2 0 -1 11 -1 3 2 -1 10 -1 0 3 -1 8 function [x, iter] = gauss_seidel(A, b, x 0, tol) U=-triu(A, 1); L=-tril(A, -1); D=diag(A)); Tgs=(D-L)U; bg = (D-L)b; imax=200; iter=imax; xold = x 0; for i=1: imax x = Tgs*xold + bg; dif = norm(x-xold); resd = norm(b-A*x); xold = x; if dif < tol & resd < tol; iter =i; break; end; end clear; clc A=[10 -1 2 0; -1 11 -1 3; 2 -1 10 -1; 0 3 -1 8]; b = [6; 25; -11; 15]; x 0=[0; 0; 0; 0]; tol=1 e-4; [x, iter] = gauss_seidel(A, b, x 0, tol)

Sec: 7. 3 The Jacobi and Gauss-Siedel Iterative Techniques