Sec 5 5 Variation of Parameters Sec 5

Sec 5. 5: Variation of Parameters

Sec 5. 5: Variation of Parameters Method ( (2 ed order) ) Solve: Step 1 Solve: Step 2 Step 3 Remark: Step 4 Make sure it is f(x) where coeff of y’’ is 1 Step 5 Step 6 Step 7 No need for constants of integration

Sec 5. 5: Variation of Parameters Method ( ) Step 1 Solve: General solution: Step 2 Step 3 Step 4 Solve IVP: Step 5 Step 6 Step 7 No need for constants of integration (2 ed order)

Sec 5. 5: Variation of Parameters (2 ed order) Method ( ) Solve: Step 1 Step 2 Why? ? ? Step 3 Step 4 Step 5 Step 6 Step 7 No need for constants of integration

Sec 5. 5: Variation of Parameters Method ( ) Solve: Step 1 Step 2 Step 3 Step 4 (Delete i-th col by Step 5 Step 6 Step 7 No need for constants of integration

Linearly independent functions Linearly Independent Linearly independent if the only solution for is Linearly Independent Linearly independent is if the only solution for

Linearly independent functions DEF: Linearly Independent Linearly independent if the only solution for is TEST: Linearly Independent using Wronskian DEF: n functions Wronskian

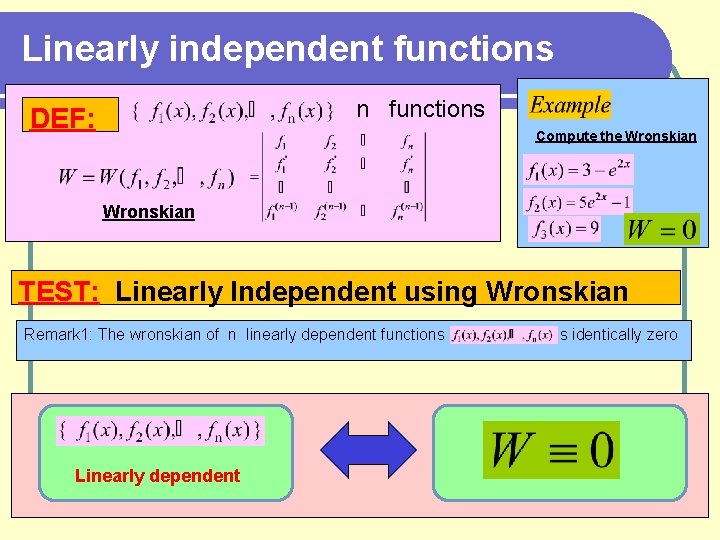
Linearly independent functions n functions DEF: Wronskian Compute the Wronskian

Linearly independent functions n functions DEF: Compute the Wronskian TEST: Linearly Independent using Wronskian Remark 1: The wronskian of n linearly dependent functions Linearly dependent is identically zero

Linearly independent functions n functions DEF: Compute the Wronskian TEST: Linearly Independent using Wronskian Remark 2: To show that the functions are linearly independent on the interval I, it suffices to show that their Wronskian is nonzero at just one point of I Linearly independent