Sec 5 4 INDEFINITE INTEGRALS AND THE NET

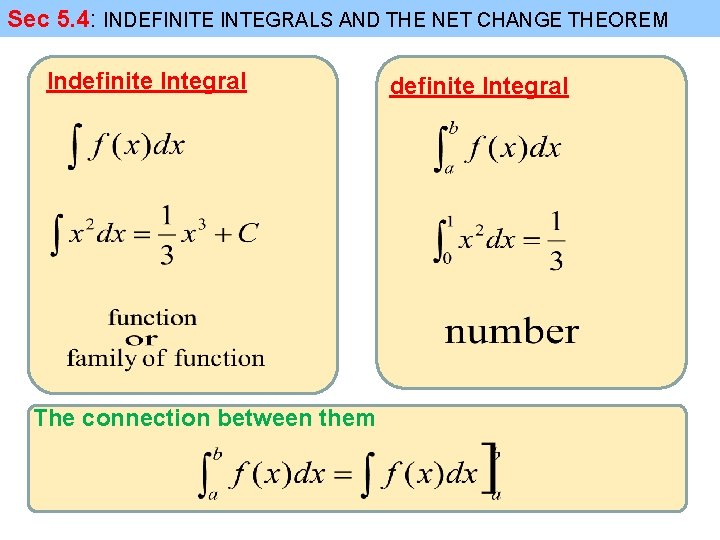
Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM Indefinite Integral Note 1: Note 2: Example: is traditionally used for an antiderivative of is called an indefinite integral

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM Indefinite Integral The connection between them definite Integral

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM TERM-092 Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM TERM-092 Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM TERM-092 Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM TERM-082 Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM TERM-082 Table Indefinite Integrals

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM represents the rate of change of represents the net change in displacement, and total distance If an object moves along a straight line with position function , then its velocity is the net change of position, or displacement,

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM displacement, and total distance If an object moves along a straight line with position function , then its velocity is the net change of position, or displacement, the net change of position = ? ? Total distance traveled = ? ?

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM displacement If an object moves along a straight line with position function , then its velocity is the net change of position, or displacement, total distance traveled

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM displacement If an object moves along a straight line with position function , then its velocity is the net change of position, or displacement, total distance traveled

Sec 5. 4: INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM