Sec 5 2 The Bisection Method Sec 5

Sec: 5. 2 The Bisection Method

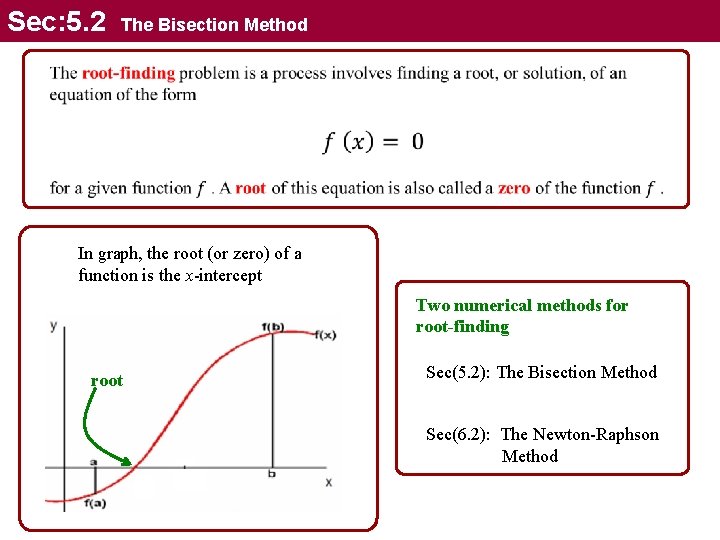
Sec: 5. 2 The Bisection Method In graph, the root (or zero) of a function is the x-intercept Two numerical methods for root-finding root Sec(5. 2): The Bisection Method Sec(6. 2): The Newton-Raphson Method

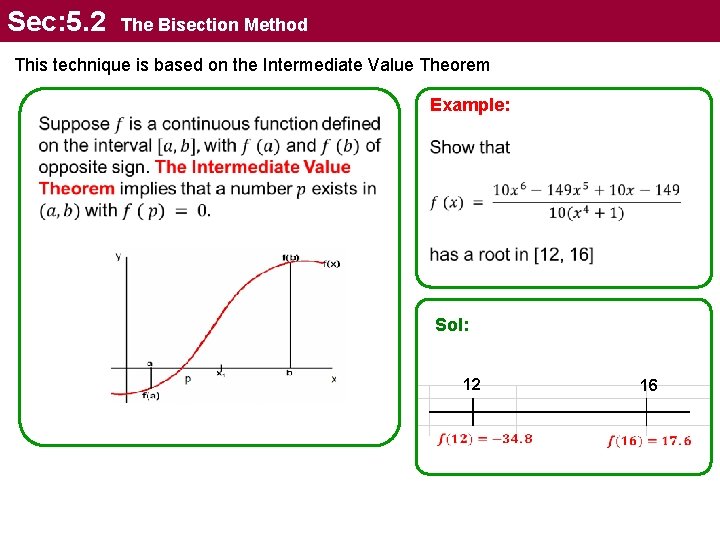
Sec: 5. 2 The Bisection Method This technique is based on the Intermediate Value Theorem Example: Sol: 12 16

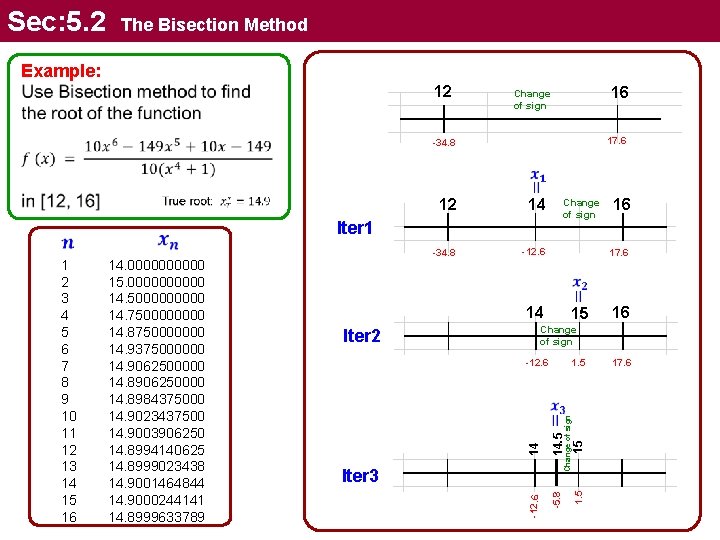
Sec: 5. 2 The Bisection Method Example: 12 16 Change of sign 17. 6 -34. 8 12 14 -34. 8 -12. 6 Change of sign Iter 1 17. 6 14 15 16 Change of sign Iter 2 1. 5 14. 5 15 -5. 8 1. 5 Change of sign -12. 6 14 14. 00000 15. 00000 14. 500000 14. 750000 14. 8750000000 14. 9375000000 14. 9062500000 14. 8906250000 14. 8984375000 14. 9023437500 14. 9003906250 14. 8994140625 14. 8999023438 14. 9001464844 14. 9000244141 14. 8999633789 Iter 3 -12. 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 16 17. 6

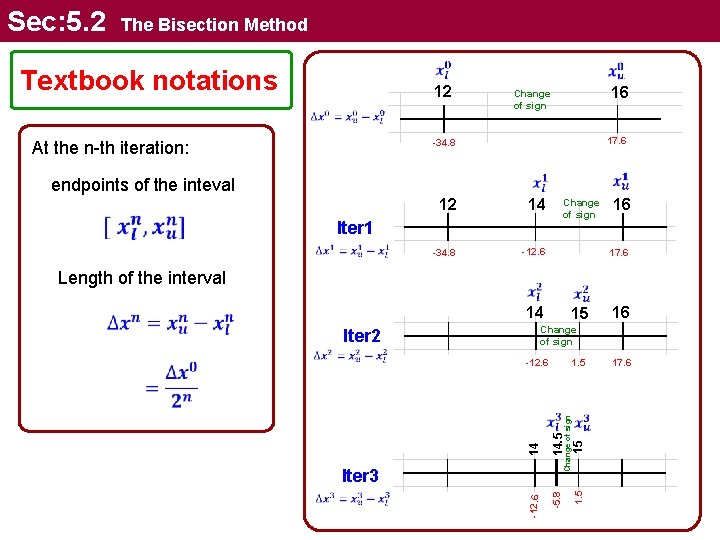
Sec: 5. 2 The Bisection Method Textbook notations 12 16 Change of sign 17. 6 -34. 8 At the n-th iteration: endpoints of the inteval 12 14 -34. 8 -12. 6 Change of sign Iter 1 16 17. 6 Length of the interval 14 15 16 Change of sign Iter 2 14. 5 15 1. 5 Change of sign 1. 5 -5. 8 14 -12. 6 Iter 3 17. 6

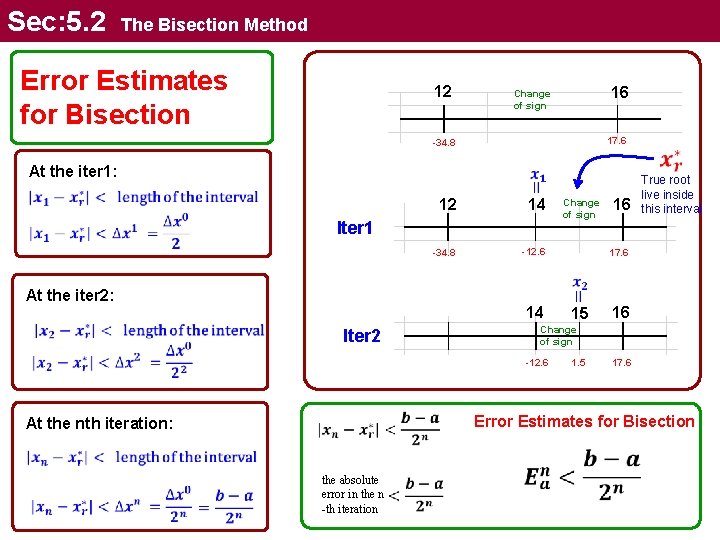
Sec: 5. 2 The Bisection Method Error Estimates for Bisection 12 16 Change of sign 17. 6 -34. 8 At the iter 1: 12 14 -34. 8 -12. 6 Iter 1 At the iter 2: 14 Iter 2 Change of sign 16 True root live inside this interval 17. 6 15 16 Change of sign -12. 6 1. 5 17. 6 Error Estimates for Bisection At the nth iteration: the absolute error in the n -th iteration

Sec: 5. 2 The Bisection Method Error Estimates for Bisection 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 14. 00000 15. 00000 14. 500000 14. 750000 14. 8750000000 14. 9375000000 14. 9062500000 14. 8906250000 14. 8984375000 14. 9023437500 14. 9003906250 14. 8994140625 14. 8999023438 14. 9001464844 14. 9000244141 14. 8999633789 -9. 00000 e-01 1. 00000 e-01 -4. 00000 e-01 -1. 500000 e-01 -2. 500000 e-02 3. 750000 e-02 6. 250000 e-03 -9. 3750000000 e-03 -1. 5625000000 e-03 2. 3437500000 e-03 3. 9062500000 e-04 -5. 8593750000 e-04 -9. 7656250000 e-05 1. 4648437500 e-04 2. 4414062500 e-05 -3. 6621093750 e-05

Sec: 5. 2 The Bisection Method Stopping Criteria function [xr, err, yc, iter, x]=bisect_ver 1(f, a, b, es) function [xr, err, yc, iter, x]=bisect_ver 2(f, a, b, es) %Input: f is the function, a, b are endpts % es is the tolerance, imax is max iter %Output: c is the zero, yc= f(c) ya=f(a); yb=f(b); iter =0; if ya*yb > 0, return, end for k=1: 1000 iter = iter +1; xr=(a+b)/2; yc=f(xr); x(k)=xr; if yc==0 a=xr; b=xr; elseif yb*yc>0 b=xr; yb=yc; else a=xr; ya=yc; end if b-a < es, break, end ya=f(a); yb=f(b); iter =0; if ya*yb > 0, return, end max 1=1+round((log(b-a)-log(es))/log(2)); for k=1: max 1 iter = iter +1; xr=(a+b)/2; yc=f(xr); x(k)=xr; if yc==0 a=xr; b=xr; elseif yb*yc>0 b=xr; yb=yc; else a=xr; ya=yc; end % if b-a < es, iter=k; break, end xr=(a+b)/2; err=abs(b-a); yc=f(xr); a=12; b=16; es=1 e-4; % [xr, err, yc, iter, x]=bisect_ver 2(f, a, b, es); [xr, err, yc, iter, x]=bisect_ver 1(f, a, b, es); iteration = [1: iter]'; res = [ iteration, x'-14. 9] fprintf(' %d %14. 10 f %14. 10 e n', res'); xr=(a+b)/2; err=abs(b-a); yc=f(xr);

Sec: 5. 2 The Bisection Method