Sec 5 1 Areas and Distances Example Formula

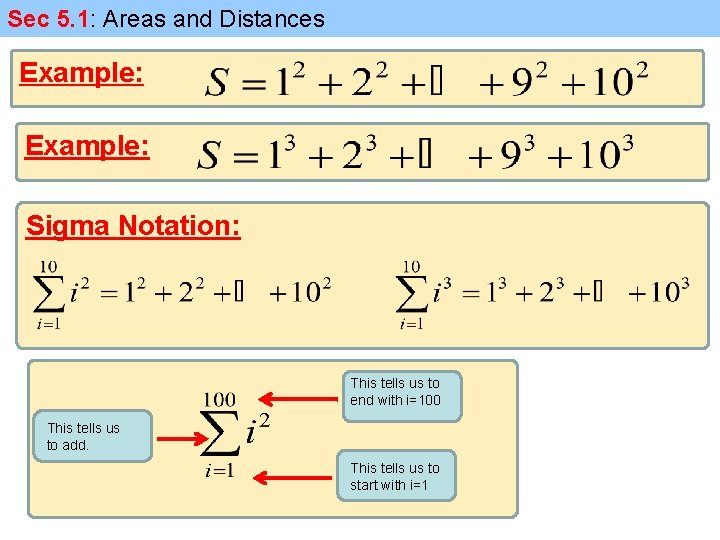
Sec 5. 1: Areas and Distances Example: Formula:

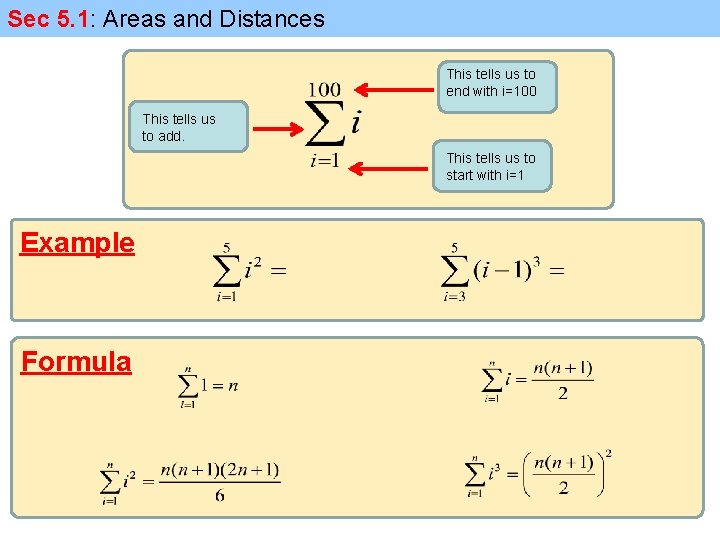
Sec 5. 1: Areas and Distances Example: Sigma Notation: This tells us to end with i=100 This tells us to add. This tells us to start with i=1

Sec 5. 1: Areas and Distances This tells us to end with i=100 This tells us to add. This tells us to start with i=1 Example Formula

Sec 5. 1: Areas and Distances

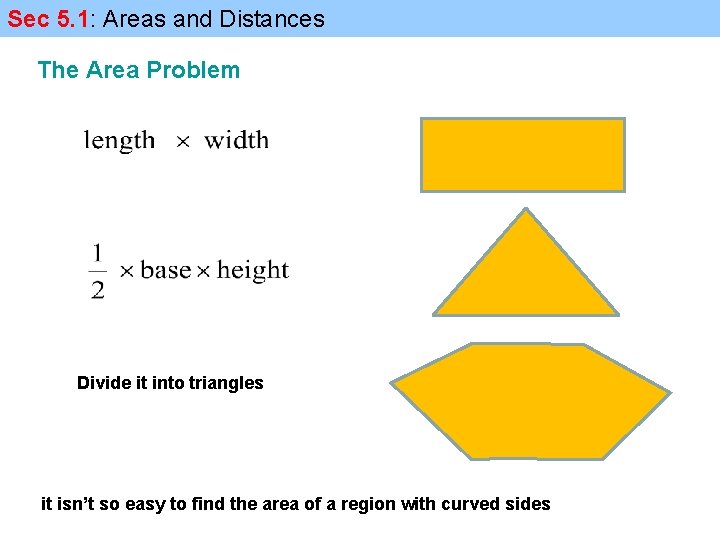
Sec 5. 1: Areas and Distances The Area Problem Divide it into triangles it isn’t so easy to find the area of a region with curved sides

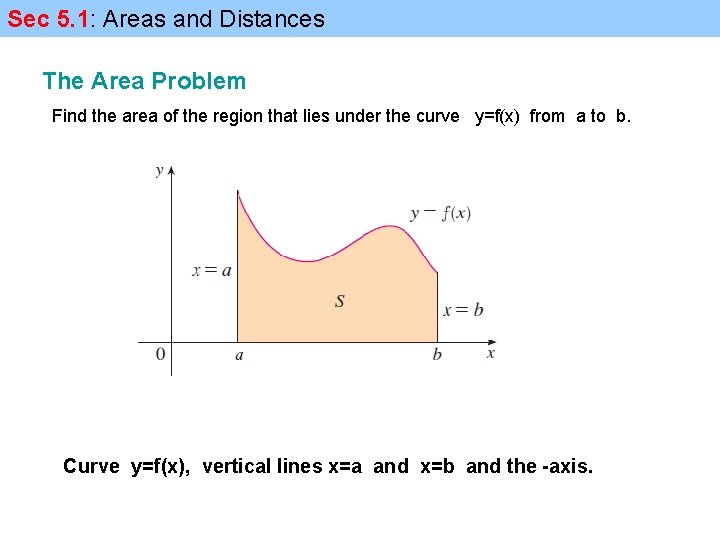
Sec 5. 1: Areas and Distances The Area Problem Find the area of the region that lies under the curve y=f(x) from a to b. Curve y=f(x), vertical lines x=a and x=b and the -axis.

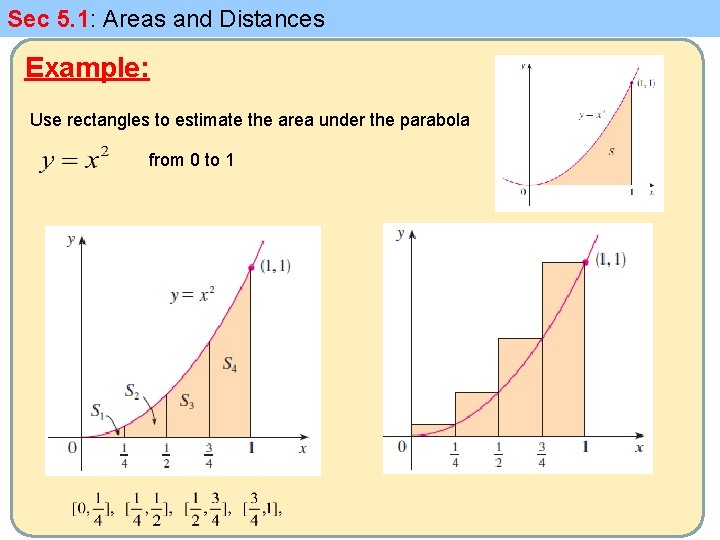
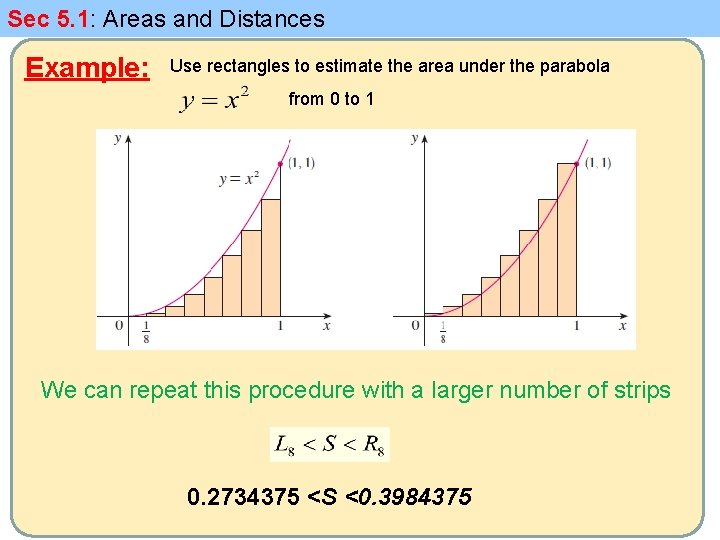
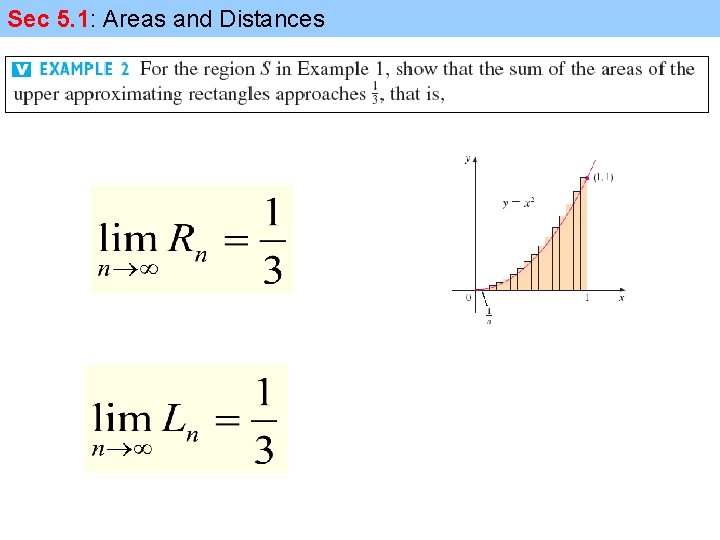
Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1

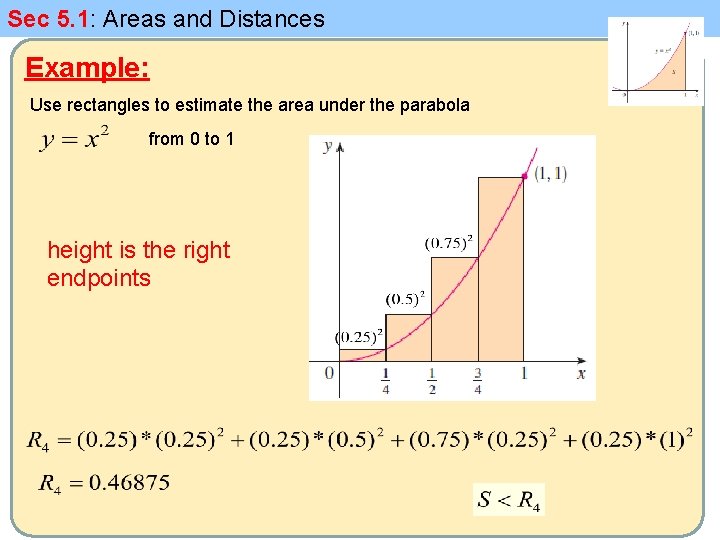
Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1 height is the right endpoints

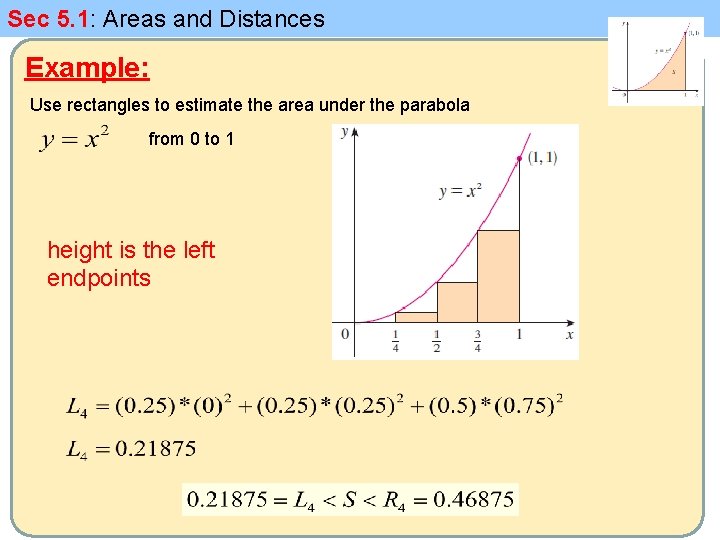
Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1 height is the left endpoints

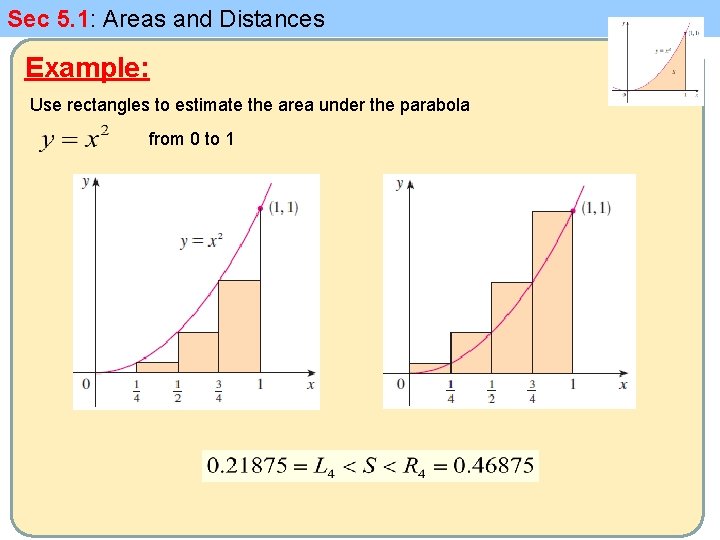
Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1

Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1 We can repeat this procedure with a larger number of strips 0. 2734375 <S <0. 3984375

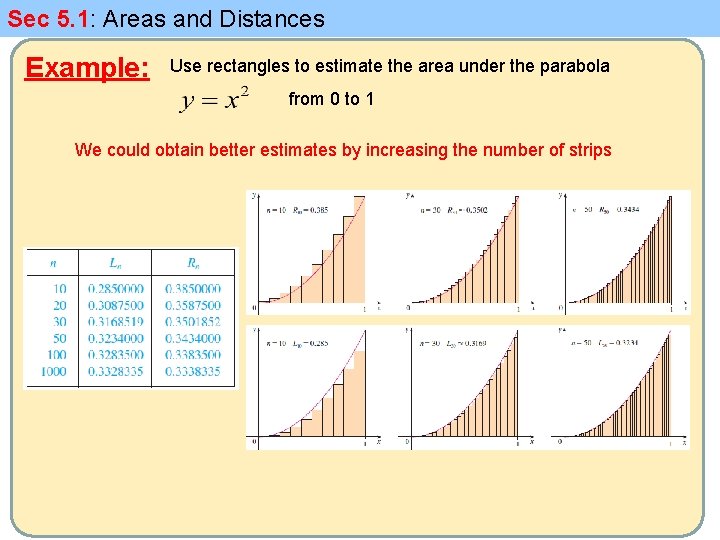
Sec 5. 1: Areas and Distances Example: Use rectangles to estimate the area under the parabola from 0 to 1 We could obtain better estimates by increasing the number of strips

Sec 5. 1: Areas and Distances Example:

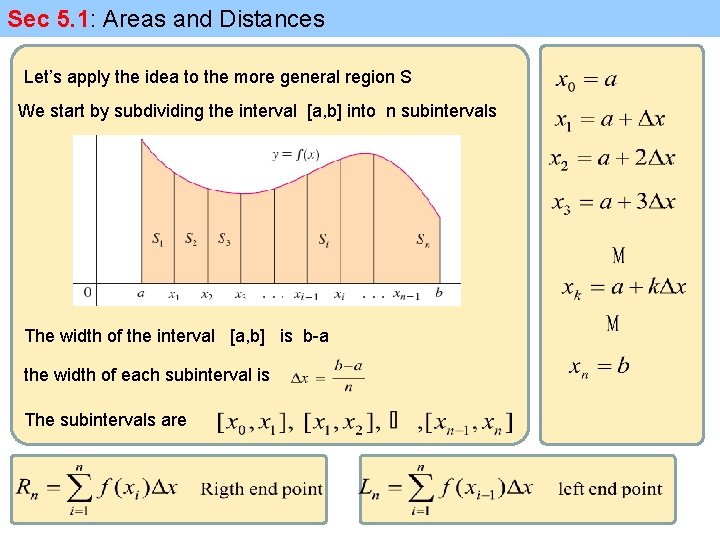
Sec 5. 1: Areas and Distances Let’s apply the idea to the more general region S We start by subdividing the interval [a, b] into n subintervals The width of the interval [a, b] is b-a the width of each subinterval is The subintervals are

Sec 5. 1: Areas and Distances

Sec 5. 1: Areas and Distances Example:

Sec 5. 1: Areas and Distances Example:

Sec 5. 1: Areas and Distances

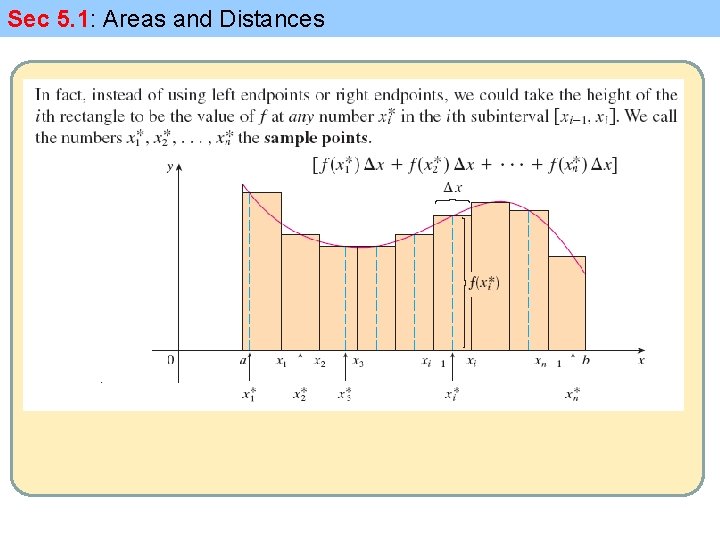
Sec 5. 1: Areas and Distances Note: Area under a curve = limit of summation Note:

Sec 5. 1: Areas and Distances HW HW

Sec 5. 1: Areas and Distances EXAM-1 TERM-102

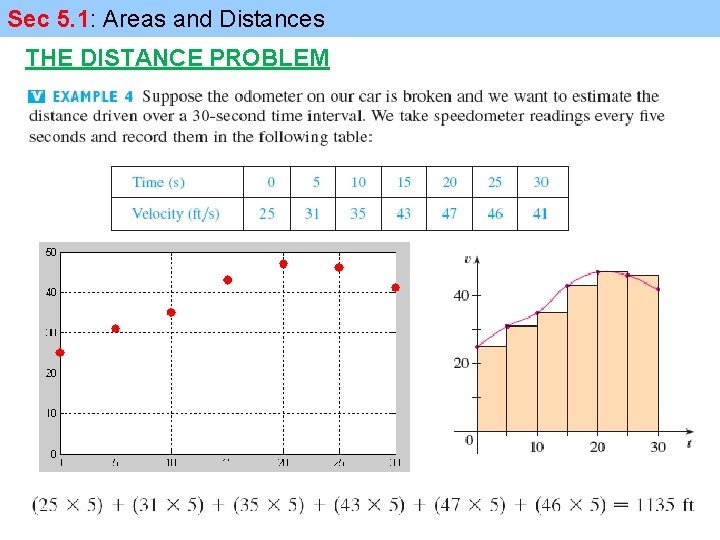
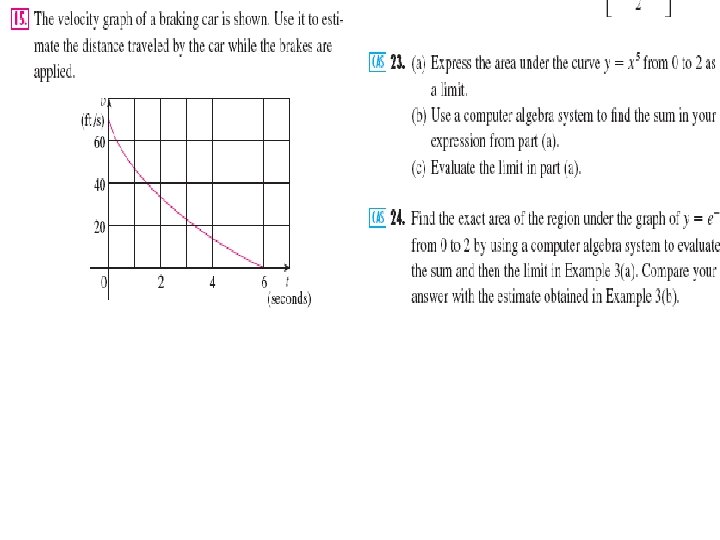
Sec 5. 1: Areas and Distances THE DISTANCE PROBLEM Find the distance traveled by an object during 10 seconds if the velocity of the object is 35 ft/s distance = velocity x time Here the velocity is constant But if the velocity varies, it’s not so easy to find the distance traveled.

Sec 5. 1: Areas and Distances THE DISTANCE PROBLEM