Sec 4 5 SUMMARY OF CURVE SKETCHING Asymptotes

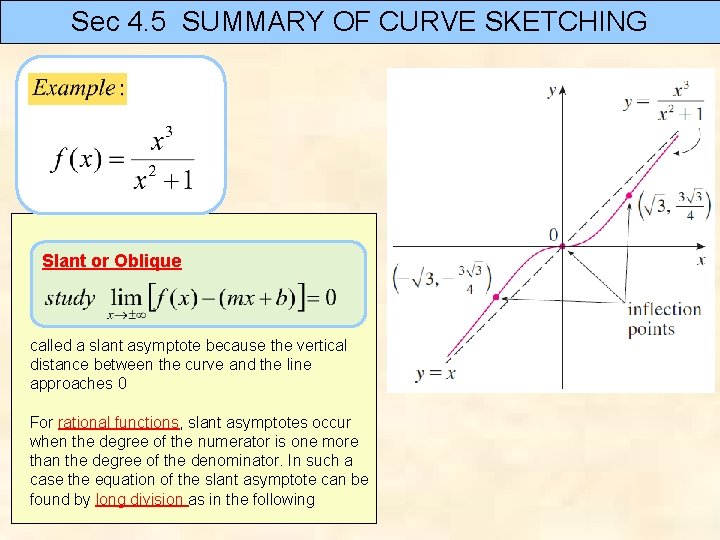
Sec 4. 5 SUMMARY OF CURVE SKETCHING Asymptotes 1)Vertical Asymptotes 2) Horizontal Asymptotes 3) Slant Asymptotes Vertical Slant or Oblique called a slant asymptote because the vertical distance between the curve and the line approaches 0. For rational functions, slant asymptotes occur when the degree of the numerator is one more than the degree of the denominator. In such a case the equation of the slant asymptote can be found by long division as in the following Horizontal

Sec 4. 5 SUMMARY OF CURVE SKETCHING Slant or Oblique called a slant asymptote because the vertical distance between the curve and the line approaches 0 For rational functions, slant asymptotes occur when the degree of the numerator is one more than the degree of the denominator. In such a case the equation of the slant asymptote can be found by long division as in the following

Sec 4. 5 SUMMARY OF CURVE SKETCHING Asymptotes 1)Vertical Asymptotes 2) Horizontal Asymptotes 3) Slant Asymptotes Horizontal Special Case: (Rational function) Horizontal or Slant Degree Example Horizontal Slant Deg(num)<Deg(den) Deg(num)=Deg(den)+1 3

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 091

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 101

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 081

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 092

Sec 4. 5 SUMMARY OF CURVE SKETCHING Slant or Oblique called a slant asymptote because the vertical distance between the curve and the line approaches 0 For rational functions, slant asymptotes occur when the degree of the numerator is one more than the degree of the denominator. In such a case the equation of the slant asymptote can be found by long division as in the following

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 101 9

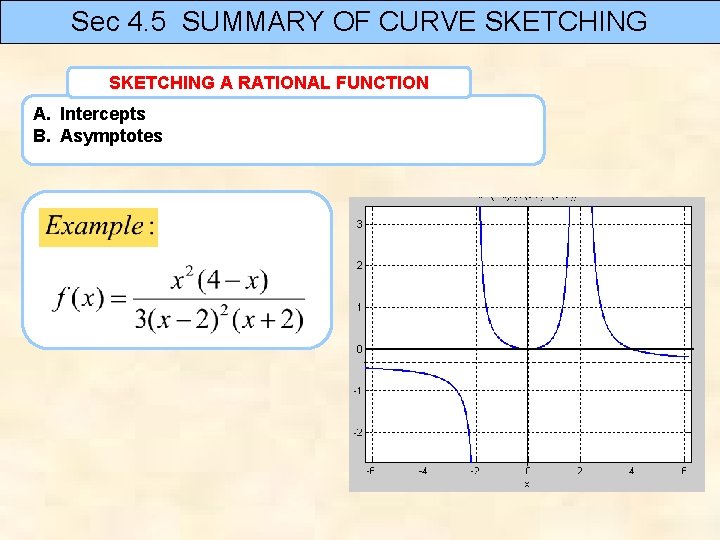
Sec 4. 5 SUMMARY OF CURVE SKETCHING A RATIONAL FUNCTION A. Intercepts B. Asymptotes

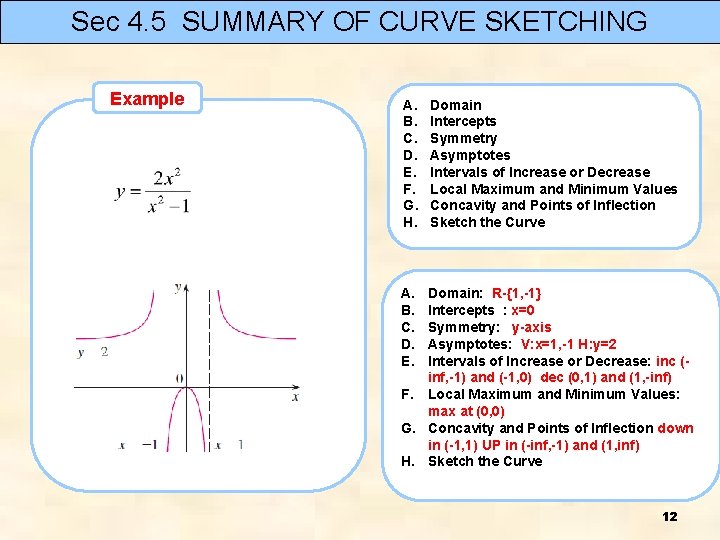
Sec 4. 5 SUMMARY OF CURVE SKETCHING GUIDELINES FOR SKETCHING A CURVE A. B. C. D. E. F. G. H. Domain Intercepts Symmetry Asymptotes Intervals of Increase or Decrease Local Maximum and Minimum Values Concavity and Points of Inflection Sketch the Curve Symmetry symmetric about the y-axis symmetric about the origin

Sec 4. 5 SUMMARY OF CURVE SKETCHING Example A. B. C. D. E. F. G. H. Domain Intercepts Symmetry Asymptotes Intervals of Increase or Decrease Local Maximum and Minimum Values Concavity and Points of Inflection Sketch the Curve A. B. C. D. E. Domain: R-{1, -1} Intercepts : x=0 Symmetry: y-axis Asymptotes: V: x=1, -1 H: y=2 Intervals of Increase or Decrease: inc (inf, -1) and (-1, 0) dec (0, 1) and (1, -inf) F. Local Maximum and Minimum Values: max at (0, 0) G. Concavity and Points of Inflection down in (-1, 1) UP in (-inf, -1) and (1, inf) H. Sketch the Curve 12

Sec 4. 5 SUMMARY OF CURVE SKETCHING F 081

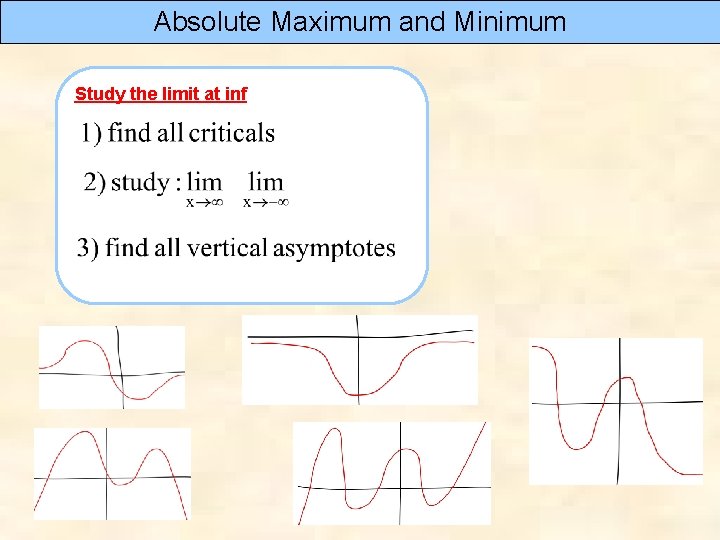
Absolute Maximum and Minimum Easy to sketch: Study the limit at inf

Absolute Maximum and Minimum Study the limit at inf

Absolute Maximum and Minimum Study the limit at inf

F 083

F 091 18

F 091 19