Sec 3 7 Implicit Differentiation Example Sec 3

Sec 3. 7: Implicit Differentiation Example:

Sec 3. 7: Implicit Differentiation Example: In some cases it is possible to solve such an equation for as an explicit function Example: In many cases it is difficult (impossible to write y in terms of x) Fortunately, we don’t need to solve an equation for y in terms of x in order to find the derivative of y. Instead we can use the method of implicit differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’.

Sec 3. 7: Implicit Differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule,

Sec 3. 7: Implicit Differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule, Example:

Sec 3. 7: Implicit Differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule, Example:

Sec 3. 7: Implicit Differentiation This consists of differentiating both sides of the equation with respect to x and then solving the resulting equation for y’. Remember: y is a function of x and using the Chain Rule,

Sec 3. 7: Implicit Differentiation Example: Remember: In finding y’’ you may use the original equation fat circle

Sec 3. 7: Implicit Differentiation 101_E 2

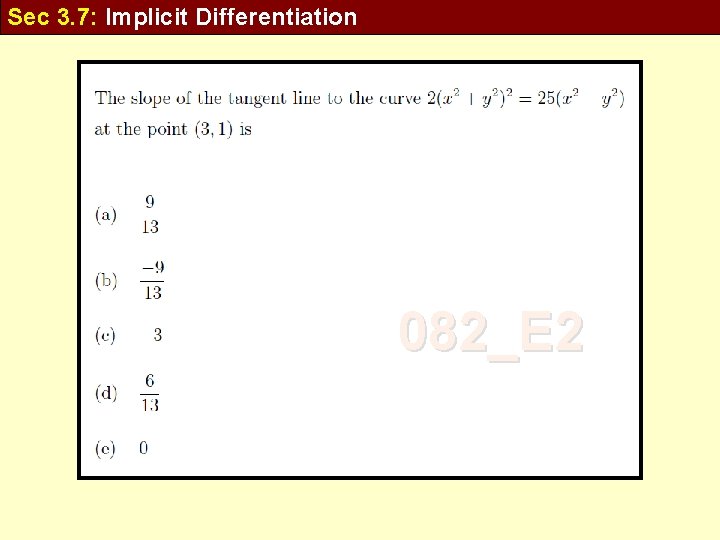
Sec 3. 7: Implicit Differentiation 082_E 2

Sec 3. 7: Implicit Differentiation 082_E 2

Sec 3. 7: Implicit Differentiation 082_E 2

Sec 3. 7: Implicit Differentiation 101_E 2

Sec 3. 7: Implicit Differentiation 093_E 2

Sec 3. 7: Implicit Differentiation 081_E 2

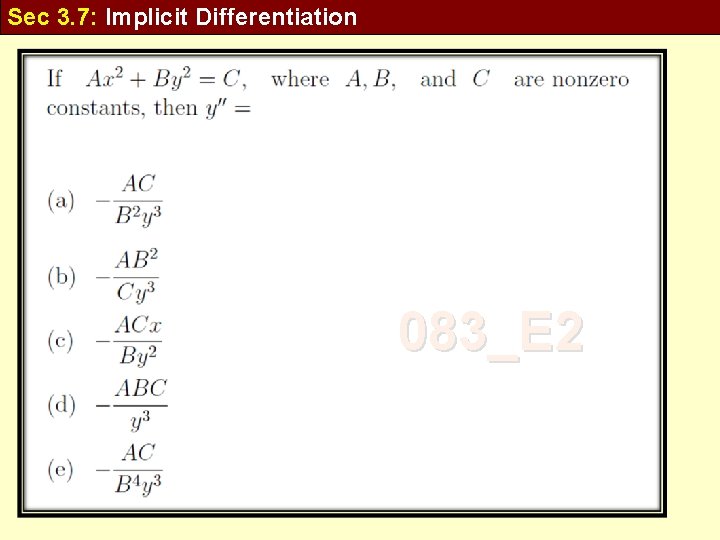
Sec 3. 7: Implicit Differentiation 083_E 2

Sec 3. 7: Implicit Differentiation 101_E 2