Sec 3 6 Determinants Sec 3 6 Determinants

Sec 3. 6 Determinants

Sec 3. 6 Determinants Recall from section 3. 5 : TH 2: the invers of 2 x 2 matrix

Sec 3. 6 Determinants 2 x 2 matrix Evaluate the determinant of How to compute the Higher-order determinants

Sec 3. 6 Determinants Def: Minors Let A =[aij] be an nxn matrix. The ijth minor of A ( or the minor of aij) is the determinant Mij of the (n-1)x(n-1) submatrix after you delete the ith row and the jth column of A. Find

Sec 3. 6 Determinants Def: Cofactors Let A =[aij] be an nxn matrix. The ijth cofactor of A ( or the cofactor of aij) is defined to be Find signs

Sec 3. 6 Determinants 3 x 3 matrix signs Find det A

Sec 3. 6 Determinants The cofactor expansion of det A along the first row of A Note: q 3 x 3 determinant q 4 x 4 determinant q 5 x 5 determinant q nxn determinant expressed in terms of three 2 x 2 determinants four 3 x 3 determinants five 4 x 4 determinants n determinants of size (n-1)x(n-1)

Sec 3. 6 Determinants nxn matrix We multiply each element by its cofactor ( in the first row) Also we can choose any row or column Th 1: the det of an nxn matrix can be obtained by expansion along any row or column. i-th row j-th column

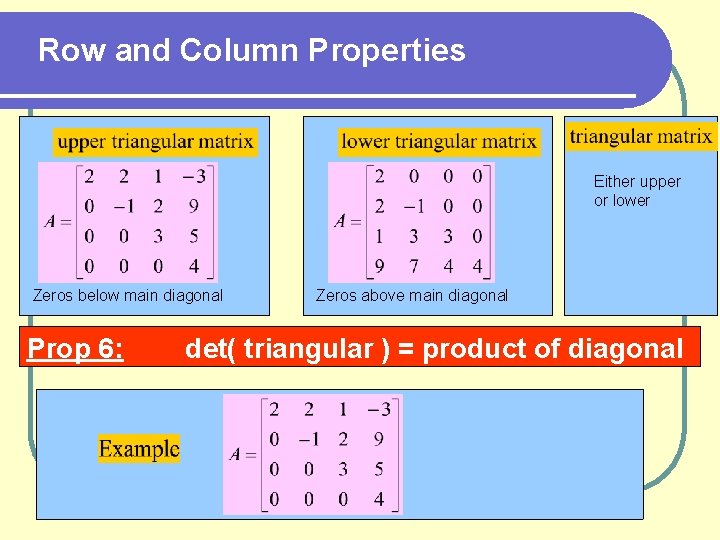
Row and Column Properties Prop 1: interchanging two rows (or columns)

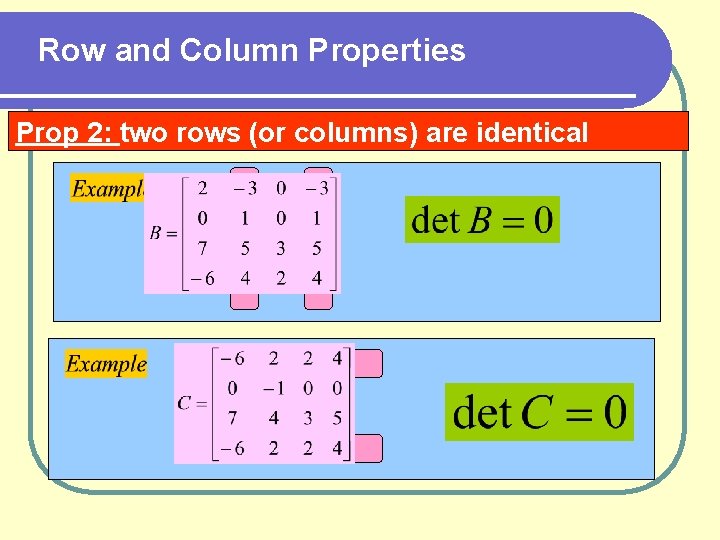
Row and Column Properties Prop 2: two rows (or columns) are identical

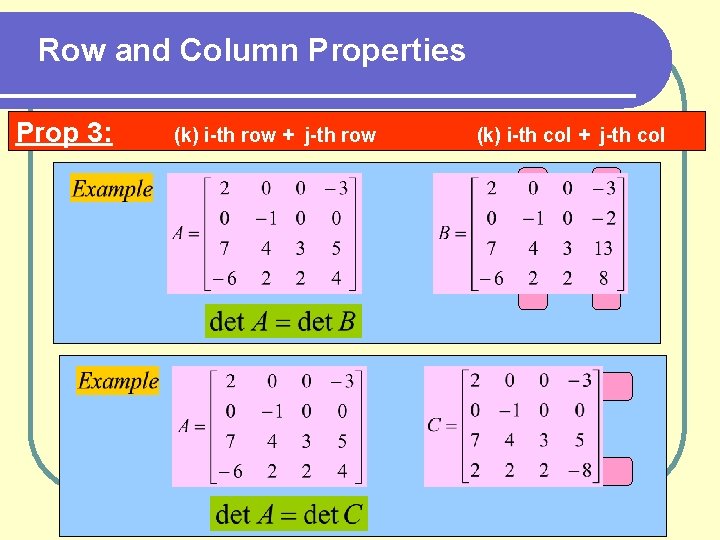
Row and Column Properties Prop 3: (k) i-th row + j-th row (k) i-th col + j-th col

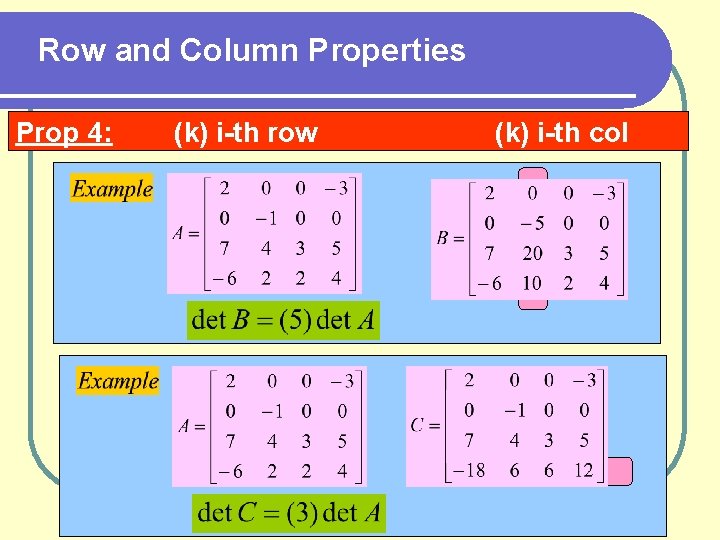
Row and Column Properties Prop 4: (k) i-th row (k) i-th col

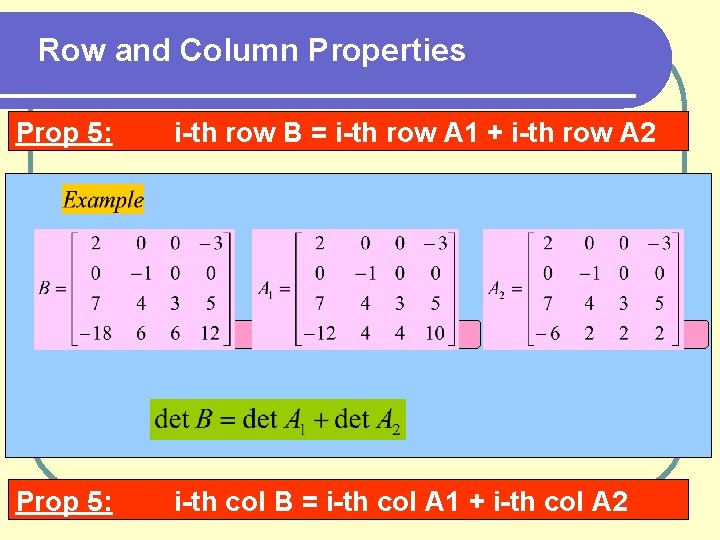
Row and Column Properties Prop 5: i-th row B = i-th row A 1 + i-th row A 2 Prop 5: i-th col B = i-th col A 1 + i-th col A 2

Row and Column Properties Either upper or lower Zeros below main diagonal Prop 6: Zeros above main diagonal det( triangular ) = product of diagonal

Row and Column Properties

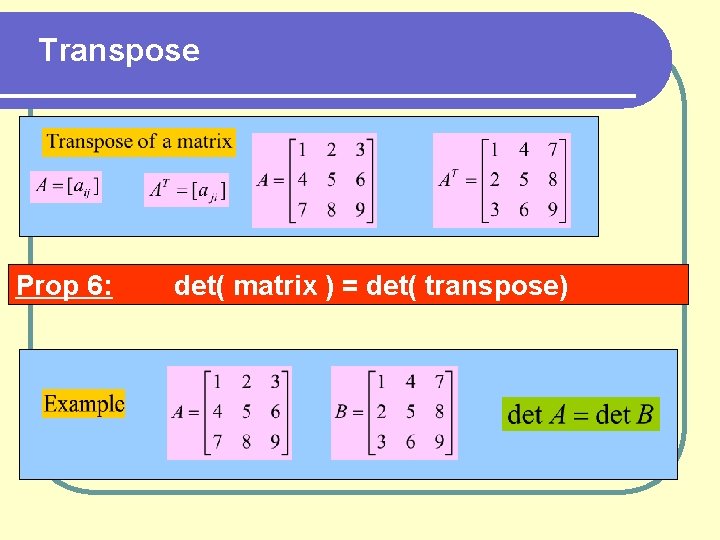
Transpose Prop 6: det( matrix ) = det( transpose)

Transpose

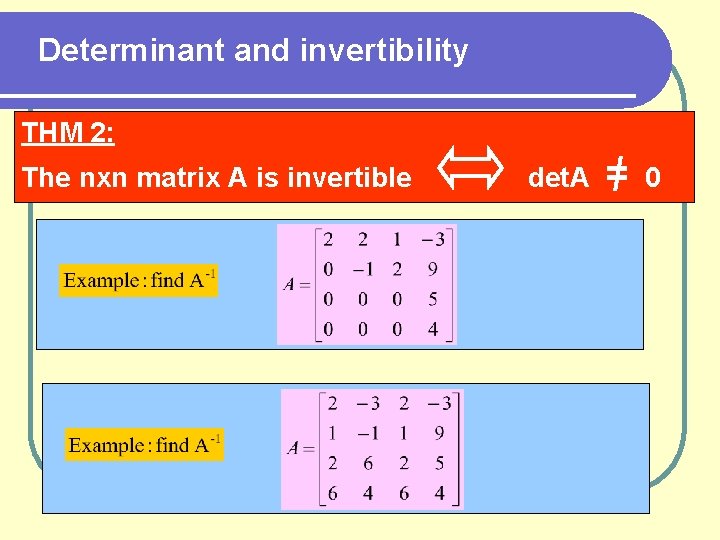
Determinant and invertibility THM 2: The nxn matrix A is invertible det. A = 0

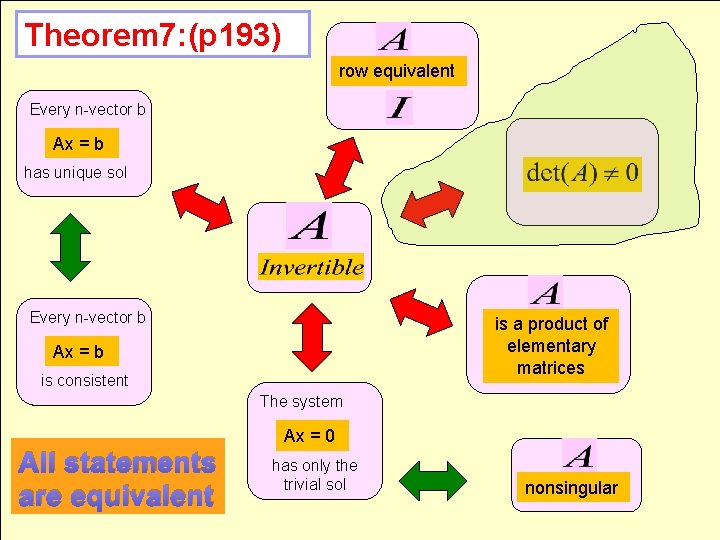
Theorem 7: (p 193) row equivalent Every n-vector b Ax = b has unique sol Every n-vector b is a product of elementary matrices Ax = b is consistent The system All statements are equivalent Ax = 0 has only the trivial sol nonsingular

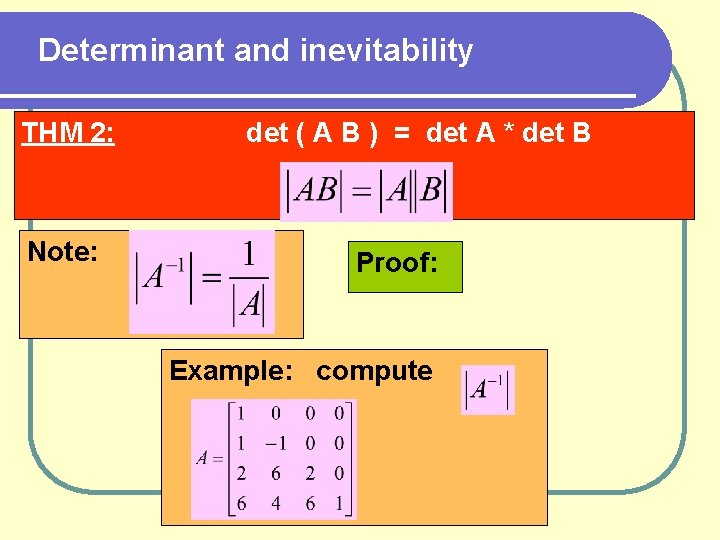
Determinant and inevitability THM 2: Note: det ( A B ) = det A * det B Proof: Example: compute

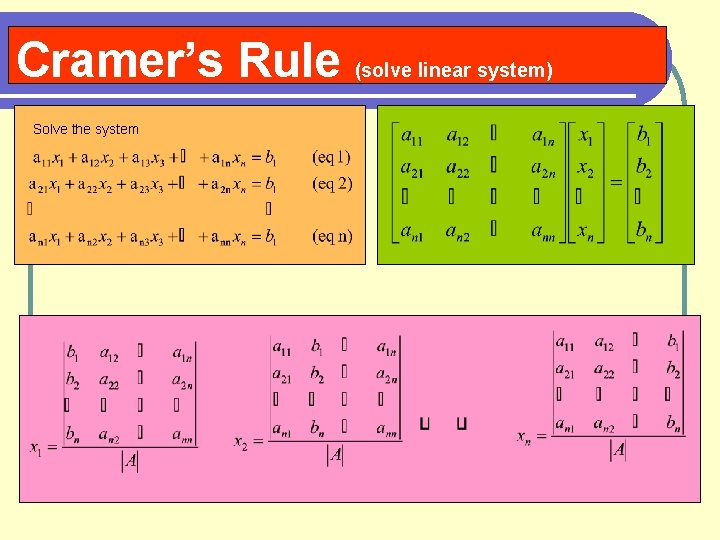
Cramer’s Rule (solve linear system) Solve the system

Sec 3. 6 Determinants Cramer’s Rule (solve linear system) Solve the system

Cramer’s Rule (solve linear system) Use cramer’s rule to solve the system

Adjoint matrix Def: Cofactor matrix Let A =[aij] be an nxn matrix. The cofactor matrix = [Aij] Find the cofactor matrix Def: Adjoint matrix of A signs Find the adjoint matrix

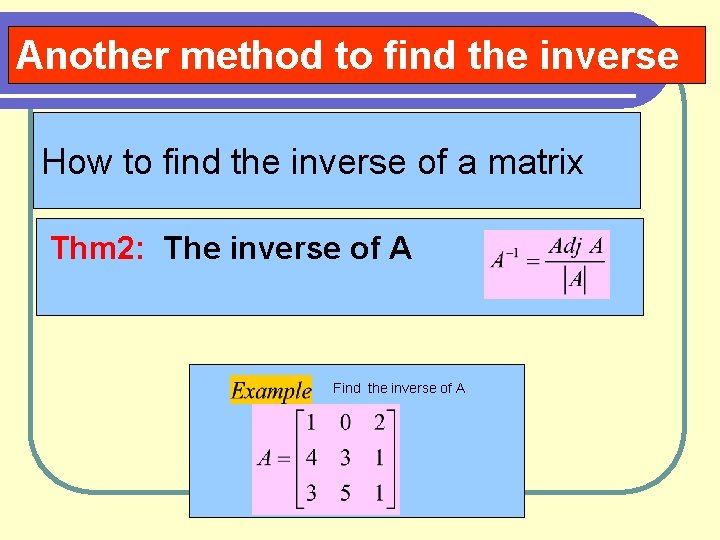
Another method to find the inverse How to find the inverse of a matrix Thm 2: The inverse of A Find the inverse of A

Computational Efficiency The amount of labor required to compute a numerical calculation is measured by the number of arithmetical operations it involves Goal: let us count just the number of multiplications required to evaluate an nxn determinant using cofactor expansion 2 x 2: 2 multiplications 3 x 3: three 2 x 2 determinants 3 x 2= 6 multiplications 4 x 4: four 3 x 3 determinants 4 x 3 x 2= 24 multiplications 5 x 5: four 3 x 3 determinants 4 x 3 x 2= 24 multiplications --------------nxn: n (n-1)x(n-1) determinants nx…x 3 x 2= n! multiplications

Computational Efficiency Goal: let us count just the number of multiplications required to evaluate an nxn determinant using cofactor expansion nxn: determinants requires n! multiplications a typical 1998 desktop computer , using MATLAB and performing only 40 million operations per second To evaluate a determinant of a 15 x 15 matrix using cofactor expansion requires a supercomputer capable of a billion operations per seconds To evaluate a detrminant of a 25 x 25 matrix using cofactor expansion requires