Sec 3 2 Linear Functions Linear Function An

Sec 3. 2 Linear Functions

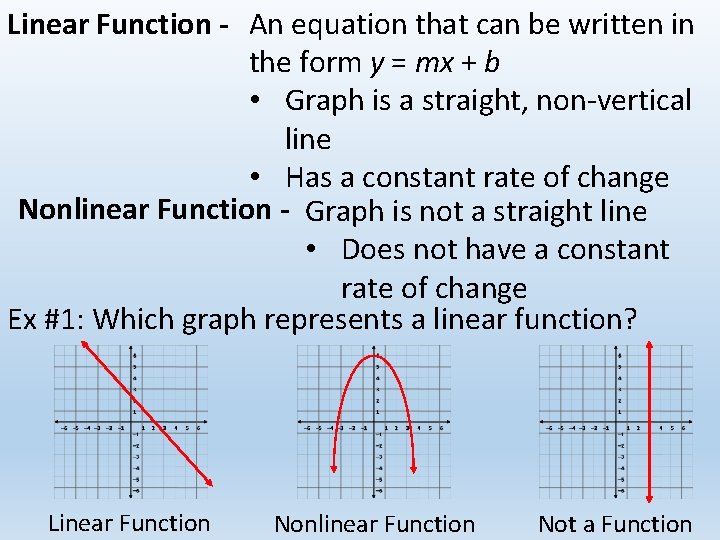
Linear Function - An equation that can be written in the form y = mx + b • Graph is a straight, non-vertical line • Has a constant rate of change Nonlinear Function - Graph is not a straight line • Does not have a constant rate of change Ex #1: Which graph represents a linear function? Linear Function Nonlinear Function Not a Function

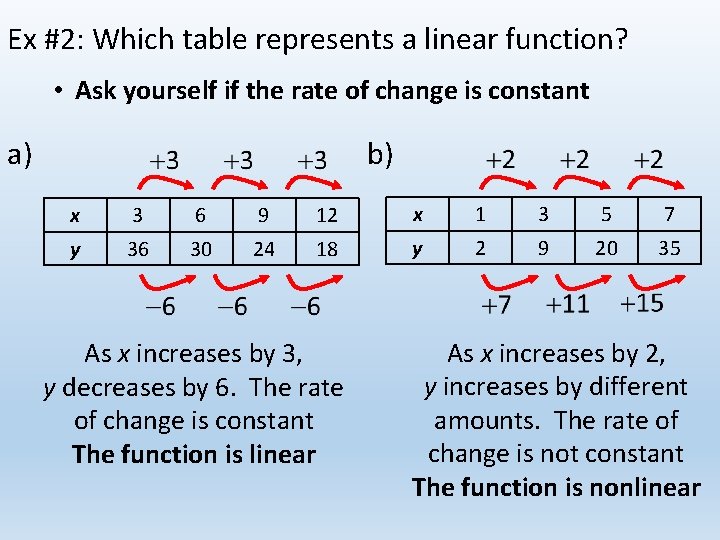
Ex #2: Which table represents a linear function? • Ask yourself if the rate of change is constant a) b) x 3 6 9 12 x 1 3 5 7 y 36 30 24 18 y 2 9 20 35 As x increases by 3, y decreases by 6. The rate of change is constant The function is linear As x increases by 2, y increases by different amounts. The rate of change is not constant The function is nonlinear

Identifying Linear Functions Using the Equations An equation represents a linear function when: • Exponents on the variables are “ 1” • No variable in denominator of a fraction • No variable under a radical (i. e. square root) • No variable as an exponent Ex #3 Which equations represent linear functions? YES NO NO NO YES

Graphing Linear Functions Solution to a linear equation in two variables – An ordered pair that makes the equation true Graph of a linear equation in two variables – The set of points that represent all the solutions of the equation Discrete Domain – A set of input values that consist of only certain numbers in an interval • Ex: 1, 2, 3, 4, 5, Continuous Domain – A set of input values that consist of all numbers in an interval • Ex: 1 ≤ x ≤ 5

The linear function y = 15. 95 x represents the cost y (in dollars) of x tickets for a museum. Each customers can buy a maximum of four tickets. a) Find the domain of the function. Is it discrete or continuous? Domain: 0, 1, 2, 3, 4 Discrete………. # of tickets must be a whole number b) Graph the function using its domain Cost (dollars) Ex #4 Number of tickets

A cereal bar contains 130 calories. The number c of calories consumed is a function of the number of b bars eaten. The function is a) Find the domain of the function. Is it discrete or continuous? Domain: b ≥ 0 Continuous………. You can eat a part of a cereal bar b) Graph the function using its domain Calories consumed Ex #5 Number of bars eaten