Sec 3 10 Linear approximation and Differentials The

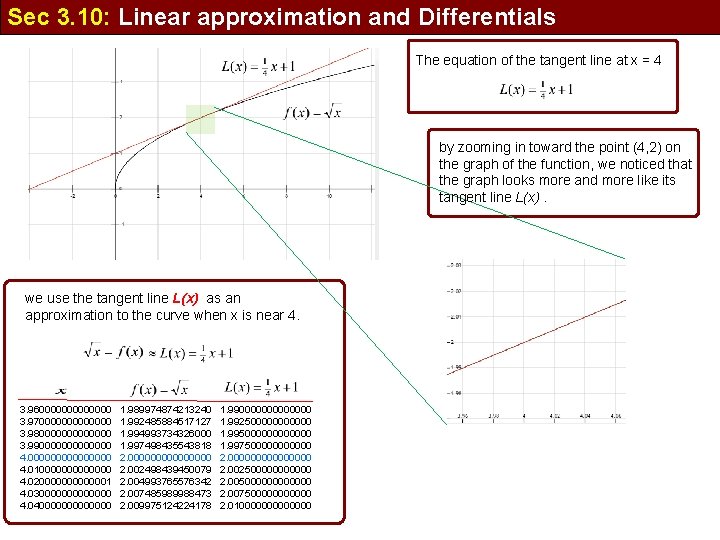
Sec 3. 10: Linear approximation and Differentials The equation of the tangent line at x = 4 by zooming in toward the point (4, 2) on the graph of the function, we noticed that the graph looks more and more like its tangent line L(x). we use the tangent line L(x) as an approximation to the curve when x is near 4. 3. 960000000 3. 970000000 3. 980000000 3. 990000000 4. 00000000 4. 010000000 4. 020000001 4. 030000000 4. 040000000 1. 989974874213240 1. 992485884517127 1. 994993734326000 1. 997498435543818 2. 00000000 2. 002498439450079 2. 004993765576342 2. 007485989988473 2. 009975124224178 1. 990000000 1. 9925000000 1. 995000000 1. 9975000000 2. 00000000 2. 0025000000 2. 005000000 2. 0075000000 2. 010000000

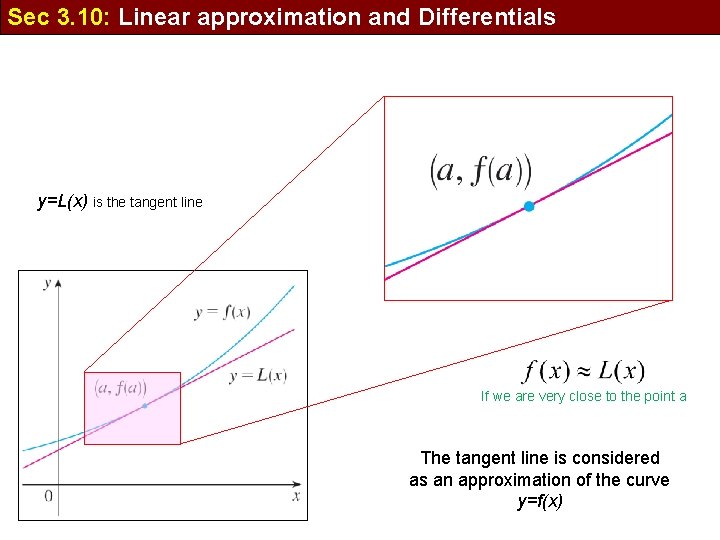
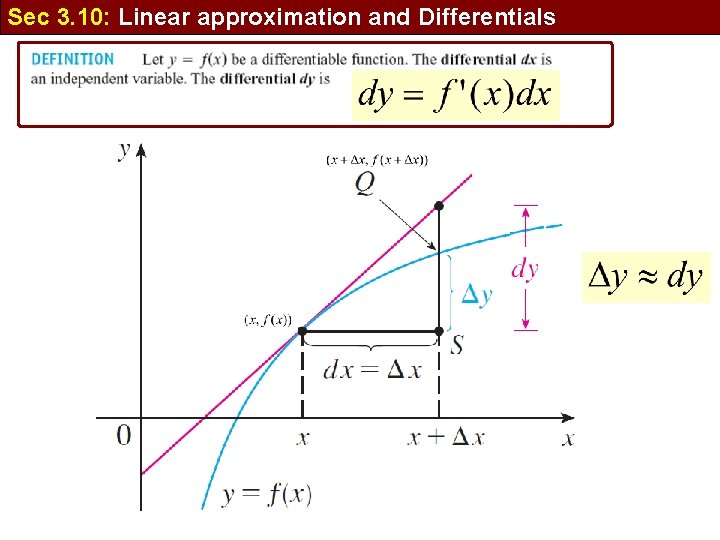
Sec 3. 10: Linear approximation and Differentials y=L(x) is the tangent line If we are very close to the point a The tangent line is considered as an approximation of the curve y=f(x)

Sec 3. 10: Linear approximation and Differentials Why do we need the approximation of f (we have f) Example: Compute: Smart Way: Find the tangent line at x=1

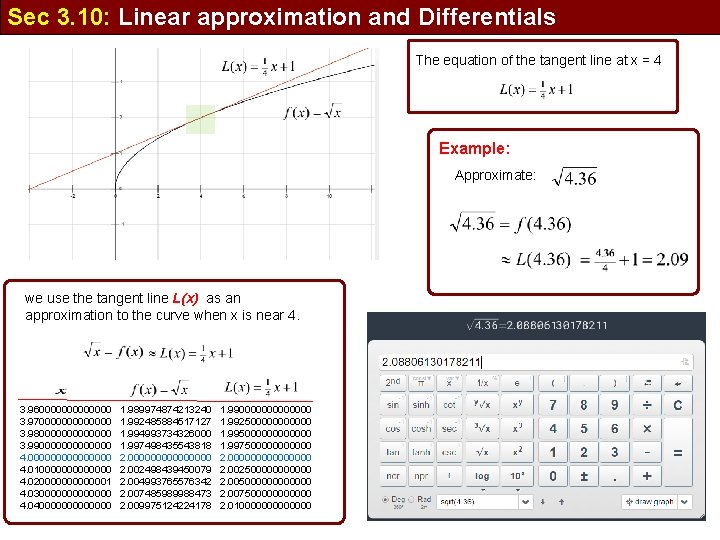
Sec 3. 10: Linear approximation and Differentials The equation of the tangent line at x = 4 Example: Approximate: we use the tangent line L(x) as an approximation to the curve when x is near 4. 3. 960000000 3. 970000000 3. 980000000 3. 990000000 4. 00000000 4. 010000000 4. 020000001 4. 030000000 4. 040000000 1. 989974874213240 1. 992485884517127 1. 994993734326000 1. 997498435543818 2. 00000000 2. 002498439450079 2. 004993765576342 2. 007485989988473 2. 009975124224178 1. 990000000 1. 9925000000 1. 995000000 1. 9975000000 2. 00000000 2. 0025000000 2. 005000000 2. 0075000000 2. 010000000

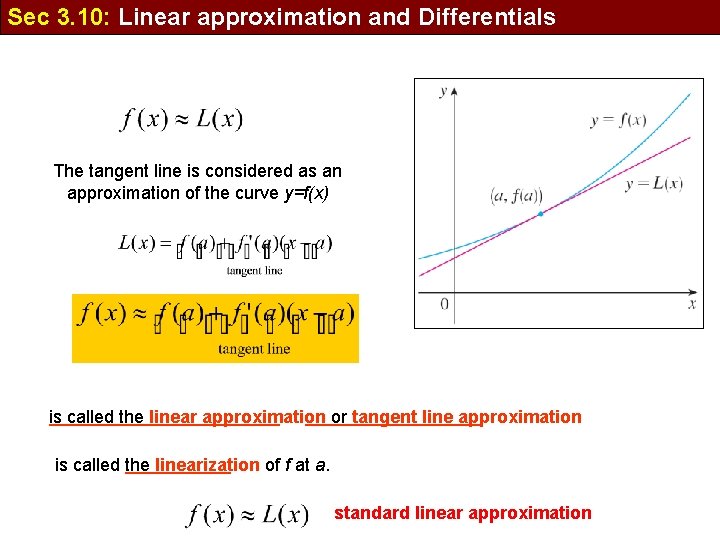
Sec 3. 10: Linear approximation and Differentials The tangent line is considered as an approximation of the curve y=f(x) is called the linear approximation or tangent line approximation is called the linearization of f at a. standard linear approximation

Sec 3. 10: Linear approximation and Differentials Example: F 091

Exa mp le: F 09 1 Sec 3. 10: Linear approximation and Differentials

Examp le: F 12 1 Sec 3. 10: Linear approximation and Differentials

Sec 3. 10: Linear approximation and Differentials

Ex am ple : 08 1 Sec 3. 10: Linear approximation and Differentials

Sec 3. 10: Linear approximation and Differentials An important linear approximation for roots and powers x sufficiently close to zero, Examples: By calculator 1. 001498876684 Examples:

Sec 3. 10: Linear approximation and Differentials APPLICATIONS TO PHYSICS Linear approximations are often used in physics. In analyzing the consequences of an equation, a physicist sometimes needs to simplify a function by replacing it with its linear approximation. x sufficiently close to zero,

Sec 3. 10 Differentials

Sec 3. 10: Linear approximation and Differentials

Sec 3. 10: Linear approximation and Differentials

Exa mpl e: 0 92 Sec 3. 10: Linear approximation and Differentials (a) 0, 014 (b) 0. 001 (c) 0. 01 (d) 0. 021 (e) 0. 045

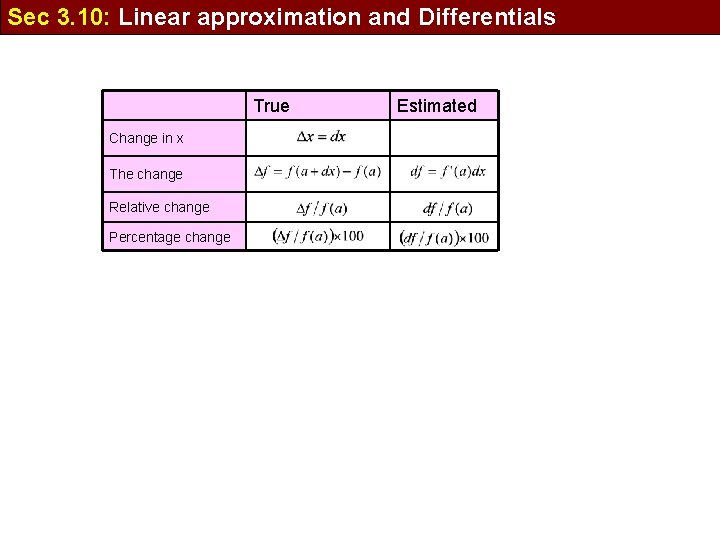
Sec 3. 10: Linear approximation and Differentials relative error percentage errors

Sec 3. 10: Linear approximation and Differentials

Sec 3. 10: Linear approximation and Differentials

Sec 3. 10: Linear approximation and Differentials True Change in x The change Relative change Percentage change Estimated