Sec 25 3 RUNGEKUTTA METHODS Sec 25 3

Sec: 25. 3 RUNGE-KUTTA METHODS

Sec: 25. 3 RUNGE-KUTTA METHODS Second-Order Runge-Kutta Methods 1) Heun Method 2) The Midpoint Method 3) Ralston’s Method I. Computational Examples II. Taylor Series Methods III. Derivations

Sec: 25. 3 RUNGE-KUTTA METHODS Initial Value Problem Euler’s Method Heun Method Euler’s Method

Sec: 25. 3 RUNGE-KUTTA METHODS Heun Method Example

Sec: 25. 3 RUNGE-KUTTA METHODS Second-Order Runge-Kutta Methods 1) Heun Method 2) The Midpoint Method 3) Ralston’s Method

Sec: 25. 3 RUNGE-KUTTA METHODS Midpoint method Example

Sec: 25. 3 RUNGE-KUTTA METHODS Second-Order Runge-Kutta Methods 1) Heun Method 2) The Midpoint Method 3) Ralston’s Method

Sec: 25. 3 RUNGE-KUTTA METHODS Ralston’s Method Example

Sec: 25. 3 RUNGE-KUTTA METHODS Heun Method Midpoint method Ralston’s Method

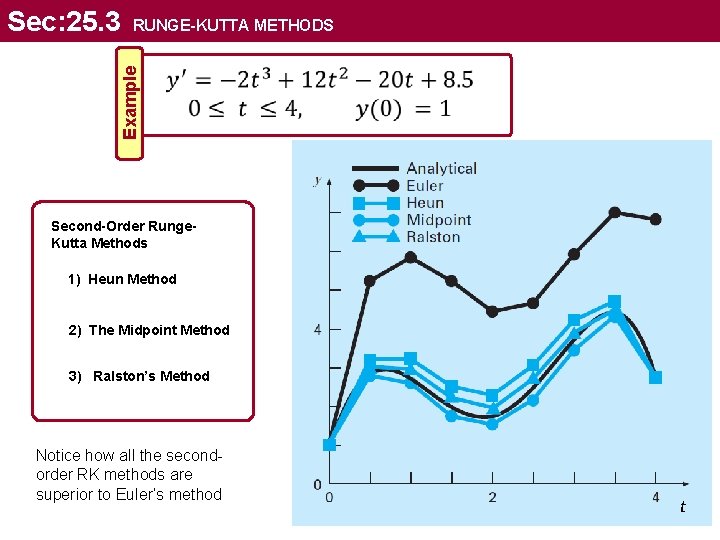
RUNGE-KUTTA METHODS Example Sec: 25. 3 Second-Order Runge. Kutta Methods 1) Heun Method 2) The Midpoint Method 3) Ralston’s Method Notice how all the secondorder RK methods are superior to Euler’s method

Sec: 25. 3 RUNGE-KUTTA METHODS clear; clc; f=@(t, y) y-t. ^2+1; alpha = 0. 5; t 0=0; h=0. 5; n=2; [w] = midpoint(t 0, h, n, alpha, f); w'; function [w] = huen(t 0, h, n, alpha, f) w(1)=alpha; t(1)=t 0; for i=1: n K 1 = f(t(i), w(i)); K 2 = f(t(i)+h, w(i)+h*K 1); w(i+1)=w(i)+(K 1+K 2)*h/2; t(i+1)=t(i)+h; end function [w] = midpoint(t 0, h, n, alpha, f) w(1)=alpha; t(1)=t 0; for i=1: n K 1 = f(t(i), w(i)) K 2 = f(t(i)+0. 5*h, w(i)+0. 5*h*K 1) w(i+1)=w(i)+(K 2)*h t(i+1)=t(i)+h; end

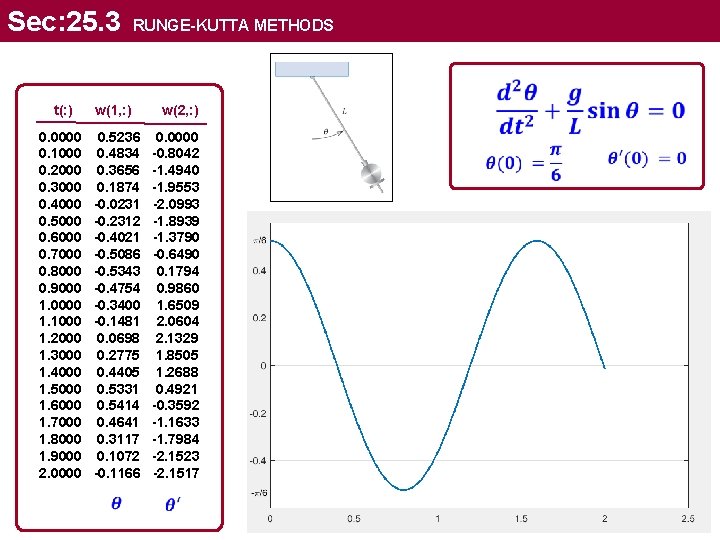
Sec: 25. 3 RUNGE-KUTTA METHODS The motion of a swinging pendulum under certain simplifying assumptions is described by the second-order differential equation Use midpoint method with h = 0. 1 s, compute the angle θ obtained for this initial-value problems at t = 0, 1, and 2 s.

Sec: 25. 3 RUNGE-KUTTA METHODS Convert into system of 1 st order ode

Sec: 25. 3 RUNGE-KUTTA METHODS Midpoint method

Sec: 25. 3 RUNGE-KUTTA METHODS clear; clc; L = 2; g=32. 17; F=@(t, Y) [ Y(2) ; . . . -(g/L)*sin(Y(1))]; t 0=0; tf=2; n=1000; h=(tf-t 0)/n; alpha = [ pi/6 ; 0 ]; [t, w] = midpoint(t 0, h, n, alpha, F); [t', w'] plot(t, w(1, : )); grid on function [t, w] = midpoint(t 0, h, n, alpha, F) w(1: 2, 1)=alpha; t(1)=t 0; for i=1: n K 1 = F(t(i), w(1: 2, i)); K 2 = F(t(i)+0. 5*h, w(1: 2, i)+0. 5*h*K 1); w(1: 2, i+1)=w(1: 2, i)+(K 2)*h; t(i+1)=t(i)+h; end Midpoint method

Sec: 25. 3 RUNGE-KUTTA METHODS t(: ) w(1, : ) 0. 0000 0. 1000 0. 2000 0. 3000 0. 4000 0. 5000 0. 6000 0. 7000 0. 8000 0. 9000 1. 0000 1. 1000 1. 2000 1. 3000 1. 4000 1. 5000 1. 6000 1. 7000 1. 8000 1. 9000 2. 0000 0. 5236 0. 4834 0. 3656 0. 1874 -0. 0231 -0. 2312 -0. 4021 -0. 5086 -0. 5343 -0. 4754 -0. 3400 -0. 1481 0. 0698 0. 2775 0. 4405 0. 5331 0. 5414 0. 4641 0. 3117 0. 1072 -0. 1166 w(2, : ) 0. 0000 -0. 8042 -1. 4940 -1. 9553 -2. 0993 -1. 8939 -1. 3790 -0. 6490 0. 1794 0. 9860 1. 6509 2. 0604 2. 1329 1. 8505 1. 2688 0. 4921 -0. 3592 -1. 1633 -1. 7984 -2. 1523 -2. 1517

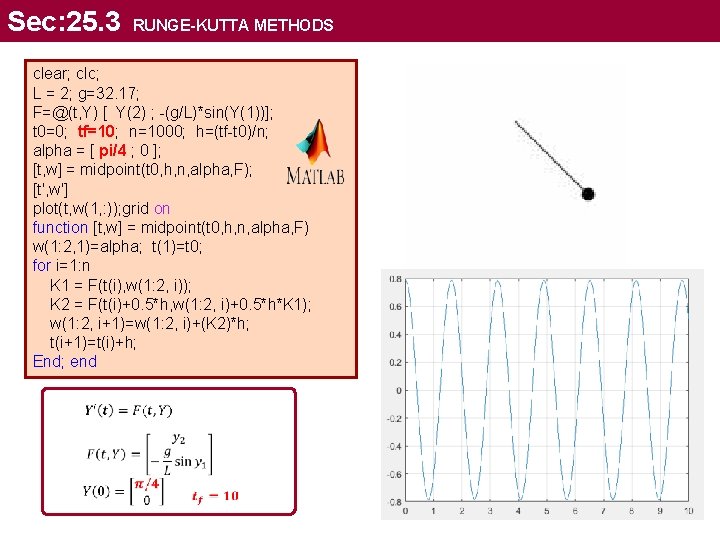
Sec: 25. 3 RUNGE-KUTTA METHODS clear; clc; L = 2; g=32. 17; F=@(t, Y) [ Y(2) ; -(g/L)*sin(Y(1))]; t 0=0; tf=10; n=1000; h=(tf-t 0)/n; alpha = [ pi/4 ; 0 ]; [t, w] = midpoint(t 0, h, n, alpha, F); [t', w'] plot(t, w(1, : )); grid on function [t, w] = midpoint(t 0, h, n, alpha, F) w(1: 2, 1)=alpha; t(1)=t 0; for i=1: n K 1 = F(t(i), w(1: 2, i)); K 2 = F(t(i)+0. 5*h, w(1: 2, i)+0. 5*h*K 1); w(1: 2, i+1)=w(1: 2, i)+(K 2)*h; t(i+1)=t(i)+h; End; end

Sec: 25. 3 RUNGE-KUTTA METHODS Second-Order Runge-Kutta Methods 1) Heun Method 2) The Midpoint Method 3) Ralston’s Method I. Computational Examples II. Taylor Series Methods III. Derivations

Sec: 25. 3 Taylor’s Series Methods RUNGE-KUTTA METHODS Euler’s Method Initial Value Problem (*) Taylor’s Series Methods One way to reduce the error of Euler’s method would be to include higher-order terms of the Taylor series expansion in the solution. Higher-order derivatives become increasingly more complicated

Sec: 25. 3 RUNGE-KUTTA METHODS Taylor’s Series Methods Taylor’s Series Method of order one Euler’s Method Taylor’s Series Method of order two

Sec: 25. 3 RUNGE-KUTTA METHODS Heun Method Midpoint method Ralston’s Method Taylor serie s in 2 -dimens ion Taylor’s Series Method of order two Matching the coefficients of f and its derivatives

Sec: 25. 3 RUNGE-KUTTA METHODS Matching the coefficients of f and its derivatives We have infinite number of solutions , there an infinite number of secondorder RK methods. three equations four unknown We present three of the most commonly used and preferred versions: Heun Method Midpoint method Ralston’s Method

Sec: 25. 3 RUNGE-KUTTA METHODS Taylor’s Series Methods Taylor’s Series Method of order three Third-Order Runge-Kutta Methods Higher order Runge-Kutta methods can be derived using the same technique.

Sec: 25. 3 RUNGE-KUTTA METHODS Taylor’s Series Method of order three The most popular method is the fourth order Runge-Kutta method, or RK 4 method Third-Order Runge-Kutta Method Fourth-Order Runge-Kutta Methods

Sec: 25. 3 RUNGE-KUTTA METHODS Implicit Euler’s Method Implicit Euler Explicit and called implicit because the unknown appears on both sides of the equation. Example Explicit Euler’s Method Implicit Euler you need to solve nonlinear equation

Sec: 25. 3 Implicit Euler Explicit and RUNGE-KUTTA METHODS Explicit Euler’s Method Implicit 2 ed order Method Implicit Euler’s Method predictor-corrector method Predictor: Corrector:

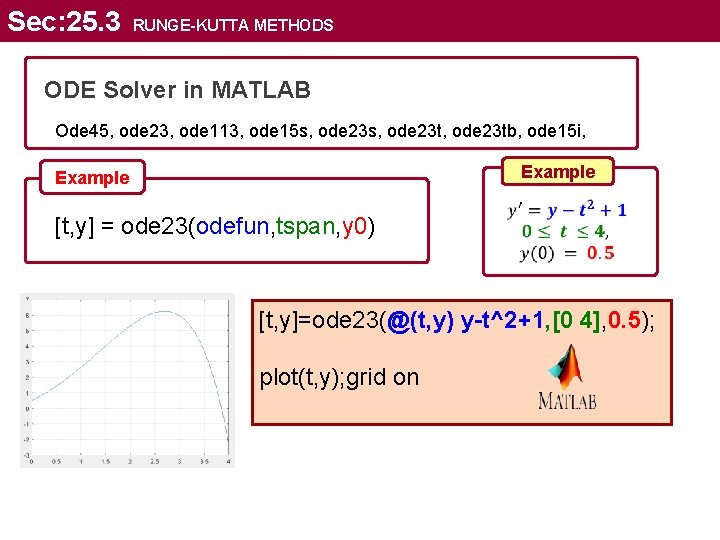
Sec: 25. 3 RUNGE-KUTTA METHODS ODE Solver in MATLAB Ode 45, ode 23, ode 113, ode 15 s, ode 23 t, ode 23 tb, ode 15 i, Example [t, y] = ode 23(odefun, tspan, y 0) [t, y]=ode 23(@(t, y) y-t^2+1, [0 4], 0. 5); plot(t, y); grid on

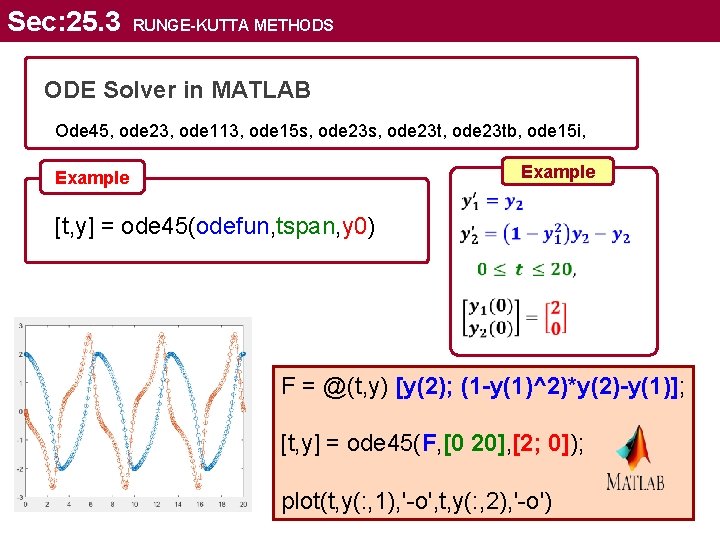
Sec: 25. 3 RUNGE-KUTTA METHODS ODE Solver in MATLAB Ode 45, ode 23, ode 113, ode 15 s, ode 23 t, ode 23 tb, ode 15 i, Example [t, y] = ode 45(odefun, tspan, y 0) F = @(t, y) [y(2); (1 -y(1)^2)*y(2)-y(1)]; [t, y] = ode 45(F, [0 20], [2; 0]); plot(t, y(: , 1), '-o', t, y(: , 2), '-o')

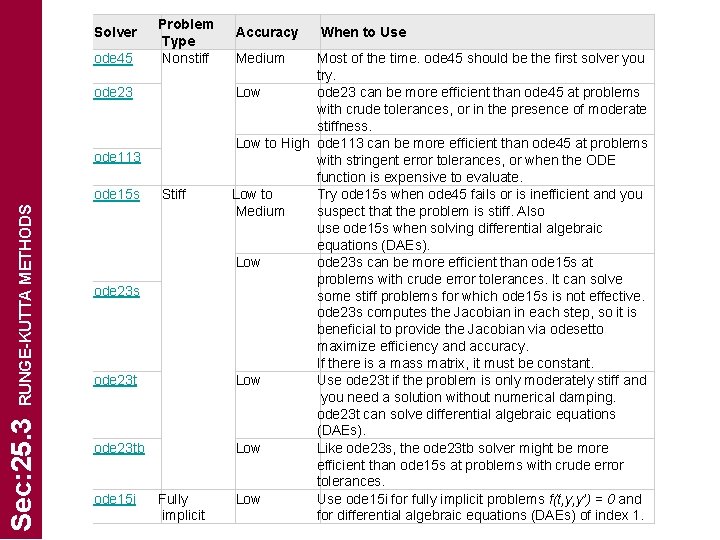
Solver ode 45 Problem Type Nonstiff ode 23 ode 113 Sec: 25. 3 RUNGE-KUTTA METHODS ode 15 s Stiff ode 23 s ode 23 tb ode 15 i Fully implicit Accuracy Medium When to Use Most of the time. ode 45 should be the first solver you try. Low ode 23 can be more efficient than ode 45 at problems with crude tolerances, or in the presence of moderate stiffness. Low to High ode 113 can be more efficient than ode 45 at problems with stringent error tolerances, or when the ODE function is expensive to evaluate. Low to Try ode 15 s when ode 45 fails or is inefficient and you Medium suspect that the problem is stiff. Also use ode 15 s when solving differential algebraic equations (DAEs). Low ode 23 s can be more efficient than ode 15 s at problems with crude error tolerances. It can solve some stiff problems for which ode 15 s is not effective. ode 23 s computes the Jacobian in each step, so it is beneficial to provide the Jacobian via odesetto maximize efficiency and accuracy. If there is a mass matrix, it must be constant. Low Use ode 23 t if the problem is only moderately stiff and you need a solution without numerical damping. ode 23 t can solve differential algebraic equations (DAEs). Low Like ode 23 s, the ode 23 tb solver might be more efficient than ode 15 s at problems with crude error tolerances. Low Use ode 15 i for fully implicit problems f(t, y, y’) = 0 and for differential algebraic equations (DAEs) of index 1.