Sec 216 Stability characteristics Euler Example consider Use

Sec 216: Stability characteristics (Euler) Example consider Use Explicit method to Estimate y(1) with stepsize: 1, 0. 001, 0. 00001, h N Y(1)

Sec 216: Stability characteristics (Euler) Example consider Use Explicit method to Estimate y(1) with stepsize: 1, 0. 001, 0. 00001, Euler Method given With h = 0. 01 the error is amplified by In 100 steps, the error in the first step is increased by 10^100 in size

Sec 216: Stability characteristics (Euler) Euler Method given With h = 0. 01 the error is amplified by In 100 steps, the error in the first step is increased by 10^100 in size Error Bound

Sec 216: Stability characteristics (Euler) Euler Method given let Stability function Implicit Euler Method given Stability function

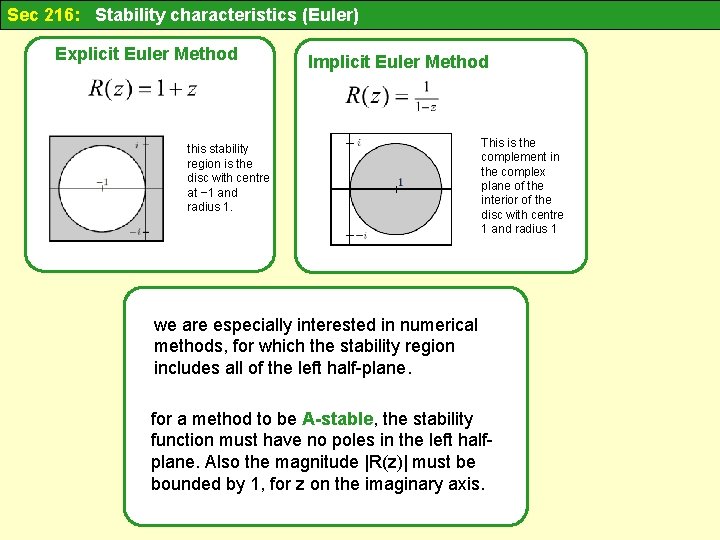
Sec 216: Stability characteristics (Euler) Explicit Euler Method Implicit Euler Method this stability region is the disc with centre at − 1 and radius 1. This is the complement in the complex plane of the interior of the disc with centre 1 and radius 1 we are especially interested in numerical methods, for which the stability region includes all of the left half-plane. for a method to be A-stable, the stability function must have no poles in the left halfplane. Also the magnitude |R(z)| must be bounded by 1, for z on the imaginary axis.

Sec 216: Stability characteristics (Euler) Runge Kutta Method Dallquist (1963) defined a method to be A-stable if the numerical solution asymptotically zero as n oo for the differential equation y’=qy, where Re(q) < 0.