Sec 2 3 Galactic Rotation Differential rotation Measured

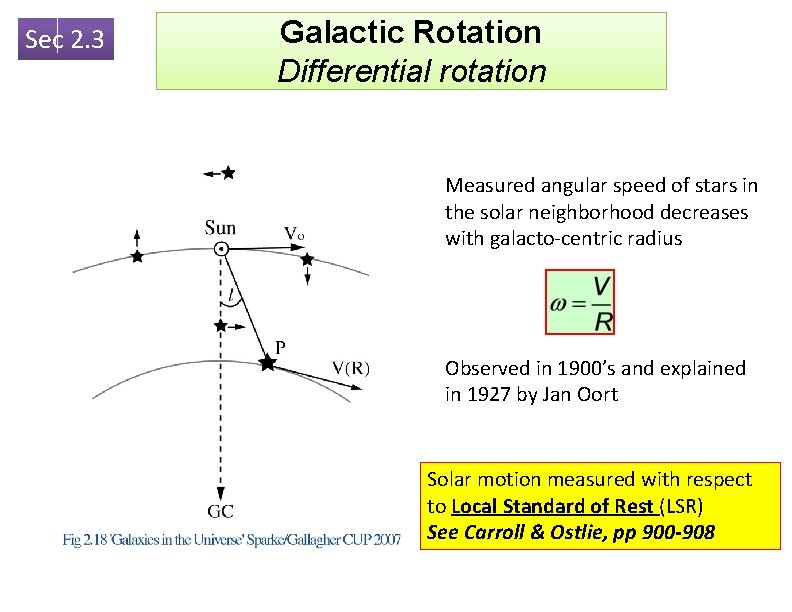
Sec 2. 3 Galactic Rotation Differential rotation Measured angular speed of stars in the solar neighborhood decreases with galacto-centric radius Observed in 1900’s and explained in 1927 by Jan Oort Solar motion measured with respect to Local Standard of Rest (LSR) See Carroll & Ostlie, pp 900 -908

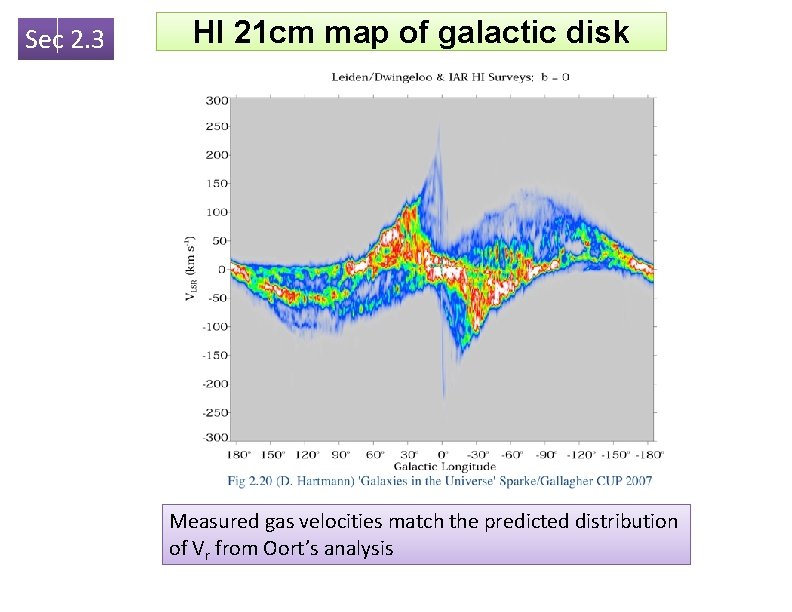
Sec 2. 3 HI 21 cm map of galactic disk Measured gas velocities match the predicted distribution of Vr from Oort’s analysis

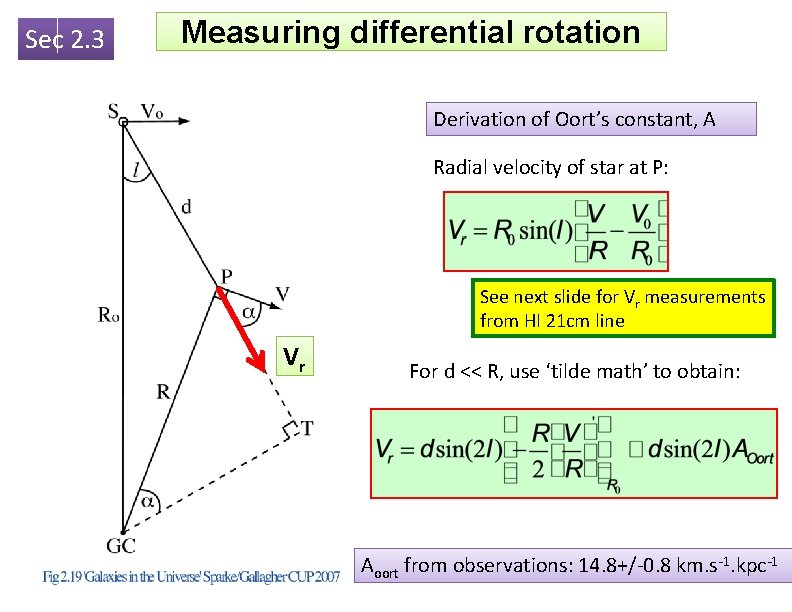
Sec 2. 3 Measuring differential rotation Derivation of Oort’s constant, A Radial velocity of star at P: See next slide for Vr measurements from HI 21 cm line Vr For d << R, use ‘tilde math’ to obtain: Aoort from observations: 14. 8+/-0. 8 km. s-1. kpc-1

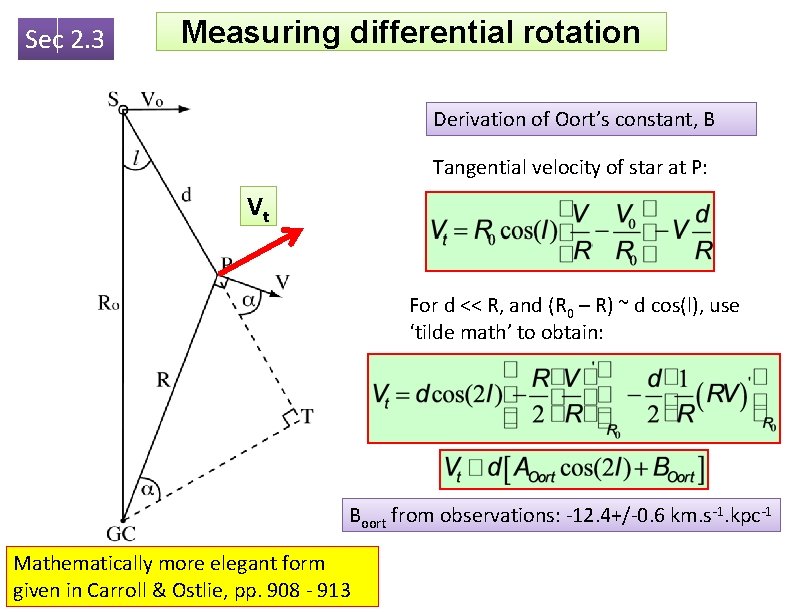
Sec 2. 3 Measuring differential rotation Derivation of Oort’s constant, B Tangential velocity of star at P: Vt For d << R, and (R 0 – R) ~ d cos(l), use ‘tilde math’ to obtain: Boort from observations: -12. 4+/-0. 6 km. s-1. kpc-1 Mathematically more elegant form given in Carroll & Ostlie, pp. 908 - 913

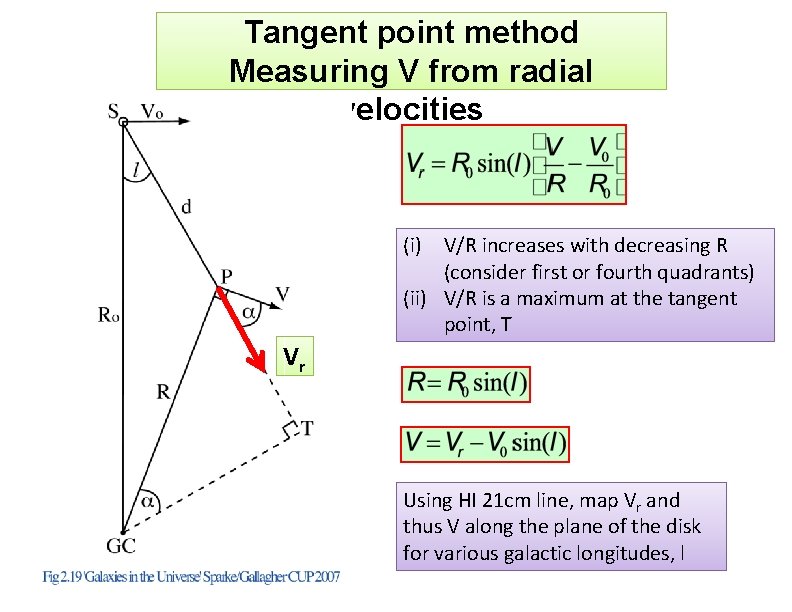
Tangent point method Measuring V from radial velocities (i) V/R increases with decreasing R (consider first or fourth quadrants) (ii) V/R is a maximum at the tangent point, T Vr Using HI 21 cm line, map Vr and thus V along the plane of the disk for various galactic longitudes, l

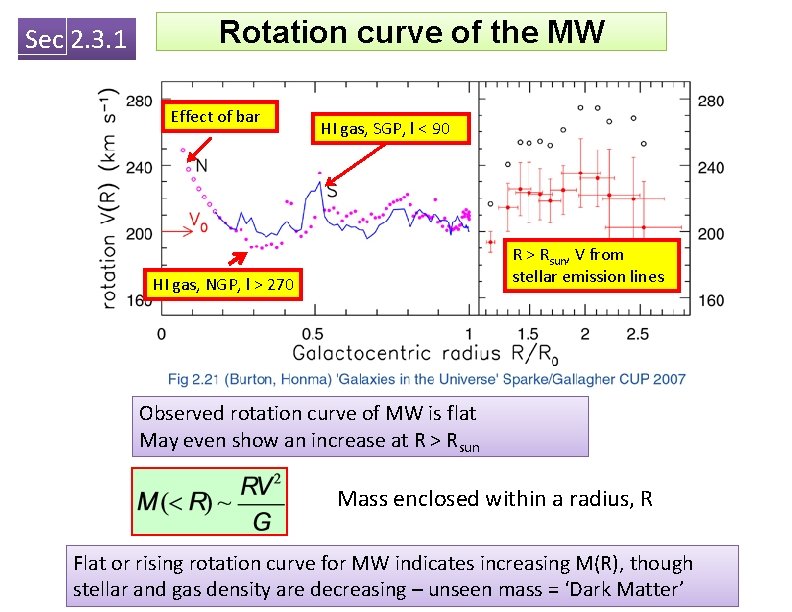
Sec 2. 3. 1 Rotation curve of the MW Effect of bar HI gas, SGP, l < 90 R > Rsun, V from stellar emission lines HI gas, NGP, l > 270 Observed rotation curve of MW is flat May even show an increase at R > Rsun Mass enclosed within a radius, R Flat or rising rotation curve for MW indicates increasing M(R), though stellar and gas density are decreasing – unseen mass = ‘Dark Matter’

Ch 3. Motion under gravity Galactic Dynamics Topics to be covered v Newton’s law of gravity v Gravitational potentials v Stellar orbital dynamics v Virial theorem v Escape velocity v Free fall and dynamical times v Two body relaxation v Epicycles v Collisionless Boltzmann equation (if time permits) Galactic Dynamics Binney, J. , & Tremaine, S. (1987) Princeton University Press.

Ch 3. Motion under gravity Galactic Dynamics Assumptions v Since interstellar distances, d >> the size (radius) of an individual star, we can treat stars as point particles for the study of their dynamics (in a galaxy) v Since the energy density in the galactic environment is small, and distances are short (compared to cosmological scales), we can neglect the effect of curvature in the geometry of space-time (no General Relativity needed) v The velocities of stars (v < 1000 km. s-1) is much smaller than the speed of light, we need not apply any relativistic corrections in our measurements of length and time (no Special Relativity needed) v Most of galactic dynamics relies on Newtonian gravitational principles only General Relativity and Cosmology (Phys 415) highly recommended!

Ch 3. Newton’s Theorems of Gravity The gravitational force inside a thin spherical shell of uniform density is zero, which implies that the potential is a constant.

Ch 3. Newton’s Theorems of Gravity Outside any spherically symmetric object, the gravitational force is the same as if all its mass had been concentrated at the center.