Sec 2 1 The Tangent Problem Example 1

Sec 2. 1: The Tangent Problem (Example 1) TERM-171

Sec 2. 1: The Tangent Problem (Example 1) TERM-172

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS From sec 2. 1 : OUR GOAL Find:

Sec 2. 2: Limit of Function and Limit Laws From sec 2. 1 : Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS 0. 5 0. 7 0. 999 1. 001 1. 2 1. 5 1. 7 1. 999 2. 001 2. 02 2. 1 2. 2 OUR GOAL we now turn our attention to limits in general and numerical and graphical methods for computing them.

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS One Sided Limit From sec 2. 1 : 0. 5 0. 8 0. 999 1. 001 1. 2 1. 5 1. 8 1. 999 2. 001 2. 02 2. 1 2. 2
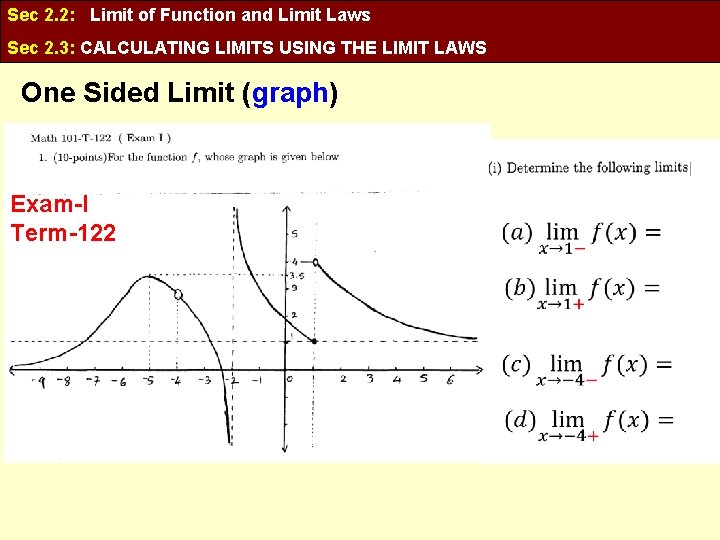
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS One Sided Limit (graph) Exam-I Term-122

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS One_Sided Limit does not exist
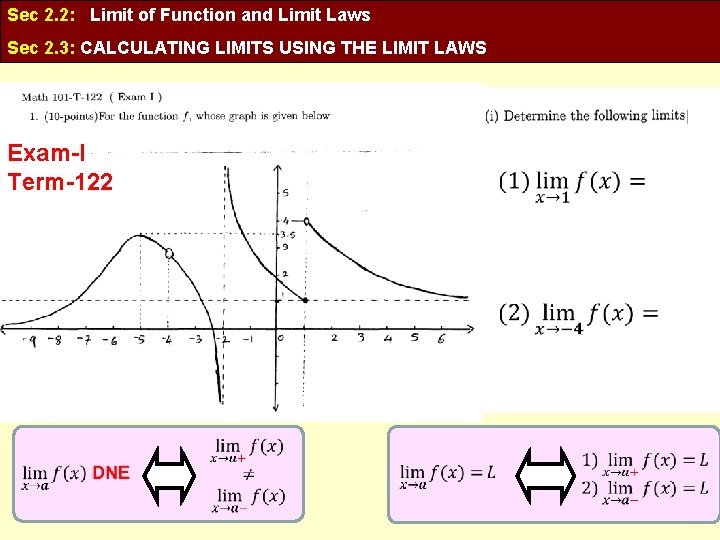
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Exam-I Term-122
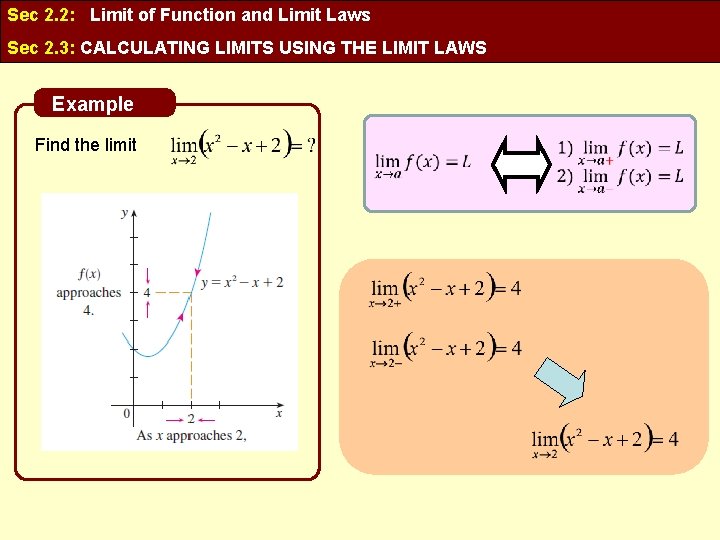
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example Find the limit
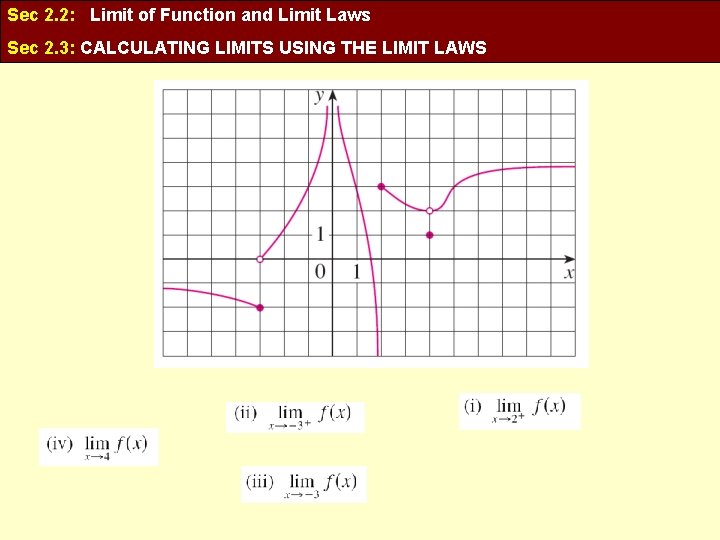
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS
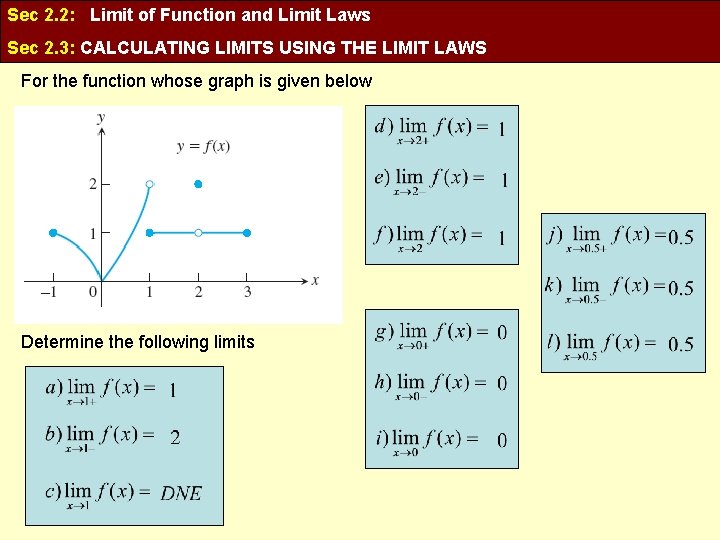
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS For the function whose graph is given below Determine the following limits

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Find: 1 Use the Graph to find the limit 2 Create a table: watch the behavior
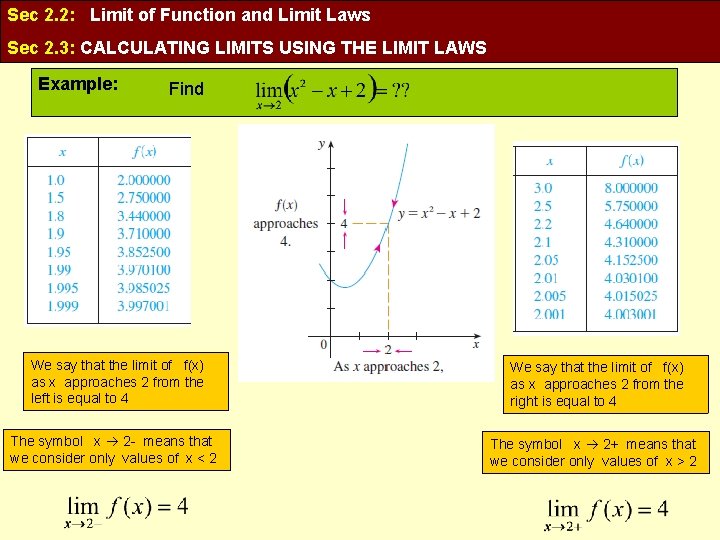
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: Find We say that the limit of f(x) as x approaches 2 from the left is equal to 4 We say that the limit of f(x) as x approaches 2 from the right is equal to 4 The symbol x 2 - means that we consider only values of x < 2 The symbol x 2+ means that we consider only values of x > 2
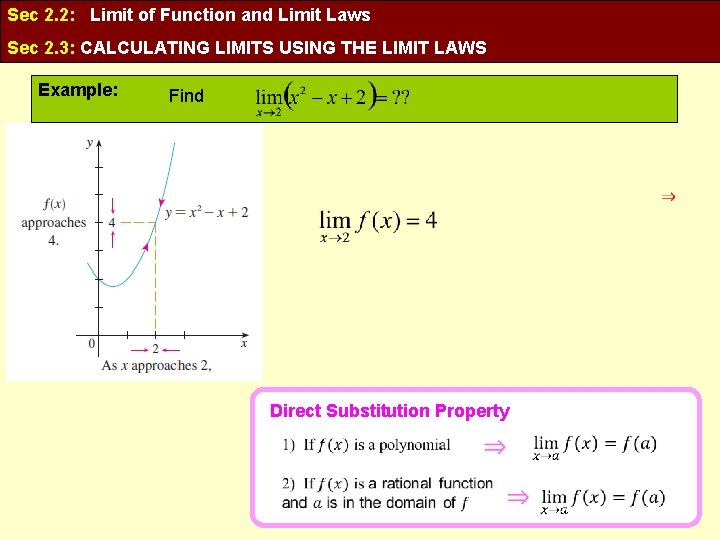
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: Find Direct Substitution Property

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: Direct Substitution Property

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS 1) Factor common factor 2) Open bracket
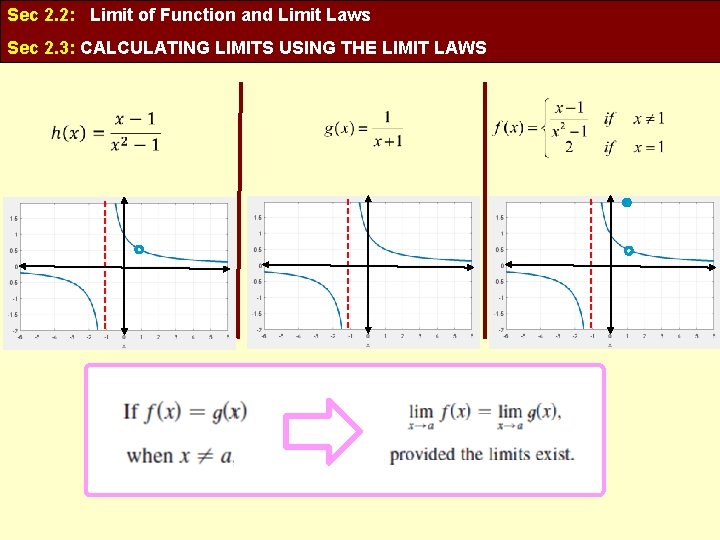
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS What is the difference ? ?

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example:

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-171

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Rationalize

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Can we use Direct Substitution Prop. ? ? -

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-171

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-172

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Can we use Direct Substitution Prop. ? ?

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Find: 1 Use the Graph to find the limit 2 Create a table: watch the behavior 3 Given the function f(x) Direct Substitution Property

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: case 1)Common Factors 2)Conjugate radical Exam-1 Term 122 Exam-1 Term 121 Example

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Absolute Value Functions

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Absolute Value Functions NOTE: 1) Study 2) In each side limit, use the definition of the absolute value

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-171

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Piecewise Functions

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS piecewise functions NOTE: 1) Study 2) In each side limit, use the definition of the piecewise function

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-172

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS The Greatest Integer functions
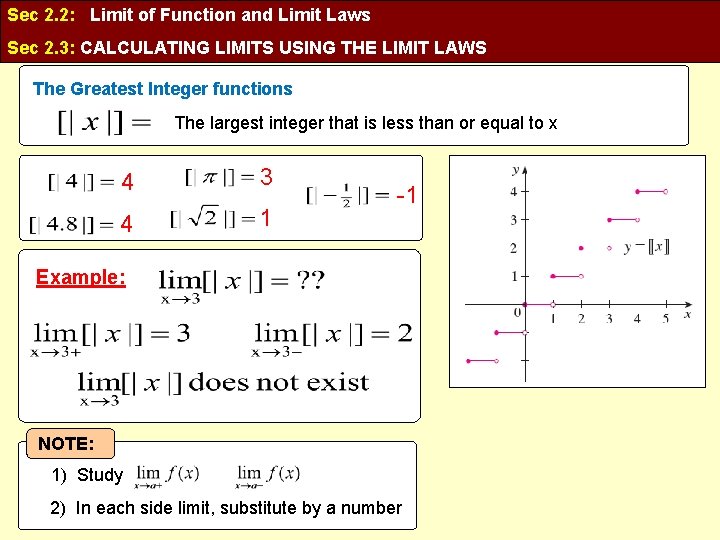
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS The Greatest Integer functions The largest integer that is less than or equal to x 4 3 4 1 -1 Example: NOTE: 1) Study 2) In each side limit, substitute by a number

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: Note: Direct substitution Check by subsuite number close from right and left Example:

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-171

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS
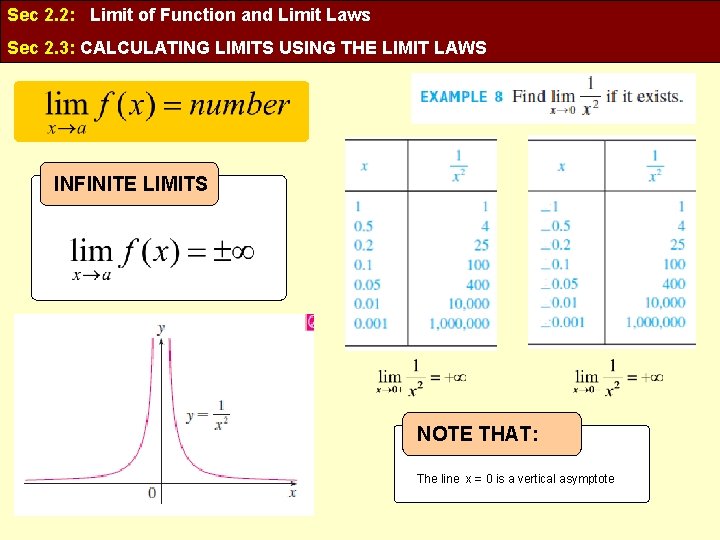
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS INFINITE LIMITS NOTE THAT: The line x = 0 is a vertical asymptote
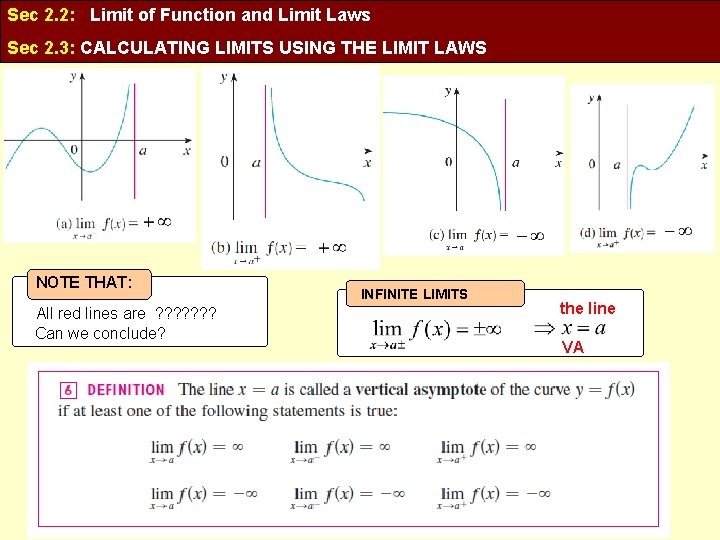
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS NOTE THAT: All red lines are ? ? ? ? Can we conclude? INFINITE LIMITS the line VA
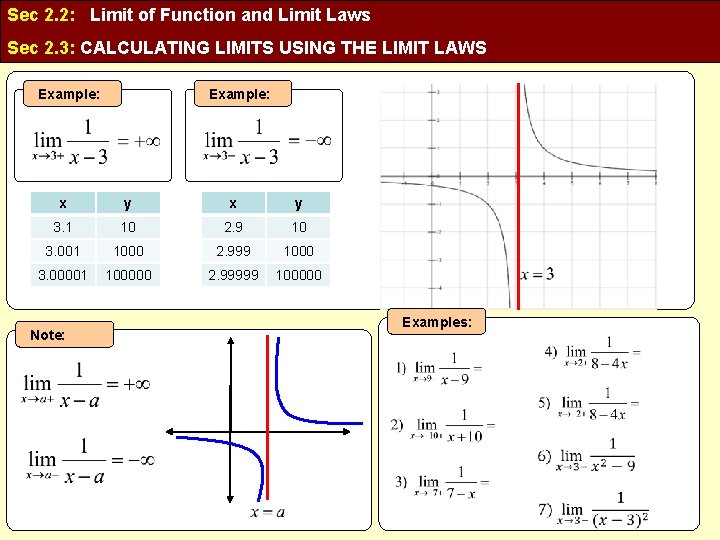
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example: x y 3. 1 10 2. 9 10 3. 001 1000 2. 999 1000 3. 00001 100000 2. 99999 100000 Note: Examples:
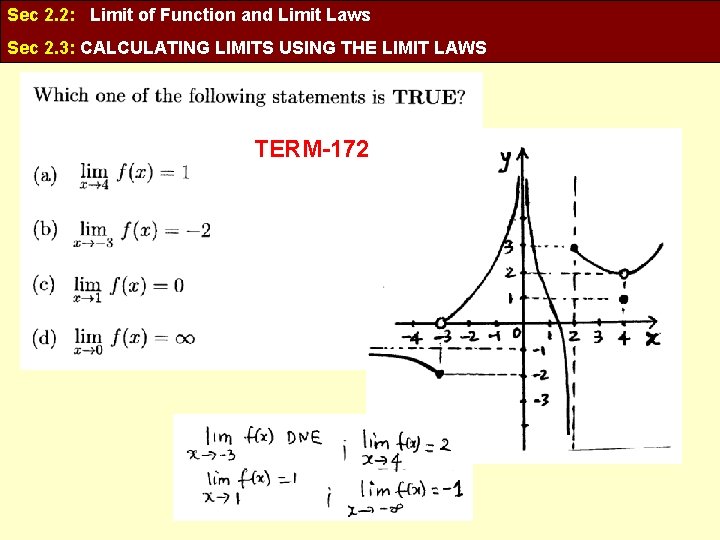
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-172

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS NOTE THAT: 1) Find the domain of f(x) 2) Study the limit 3) If the limit is + or - infinity

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-173

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Rational function

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Rational function (substitute by a) 1)Common Factors 2)Open brackets 3)……. . Direct substitution

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS The Squeeze Theorem
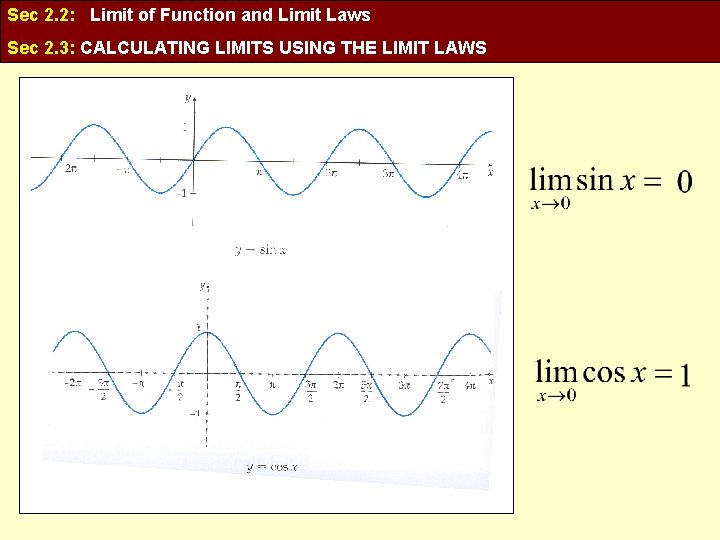
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS
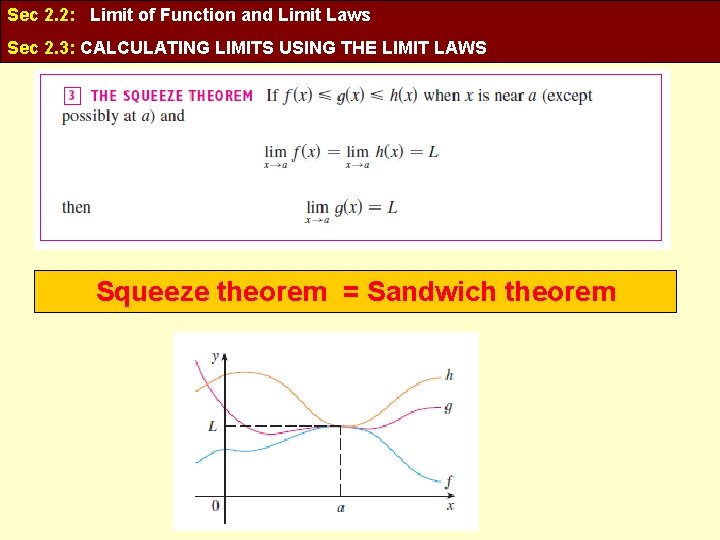
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Squeeze theorem = Sandwich theorem
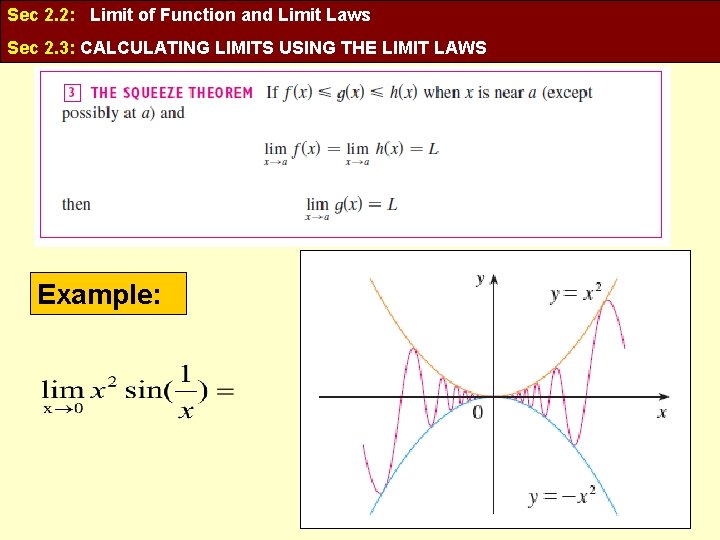
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example:

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-171

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS TERM-172

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Exam 1 -091
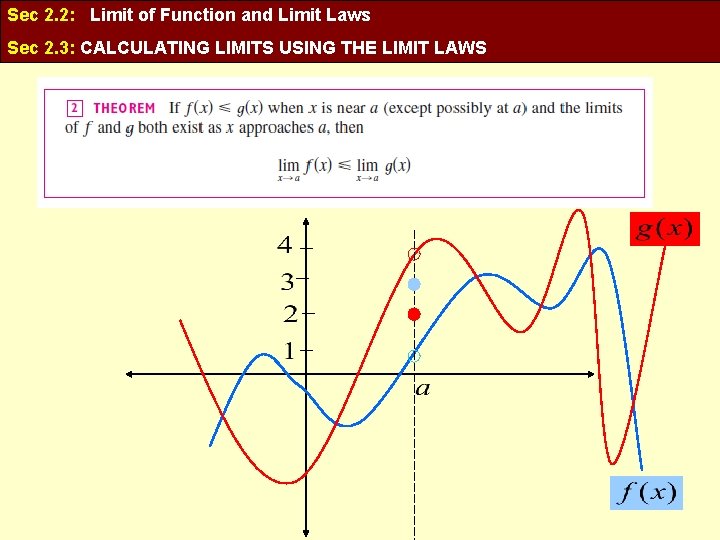
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS One. Sided limit DNE
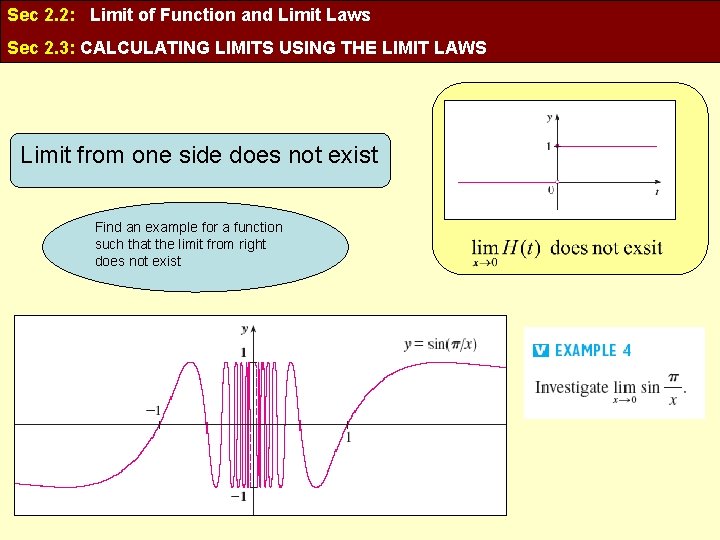
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Limit from one side does not exist Find an example for a function such that the limit from right does not exist

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Example

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Other Known functions
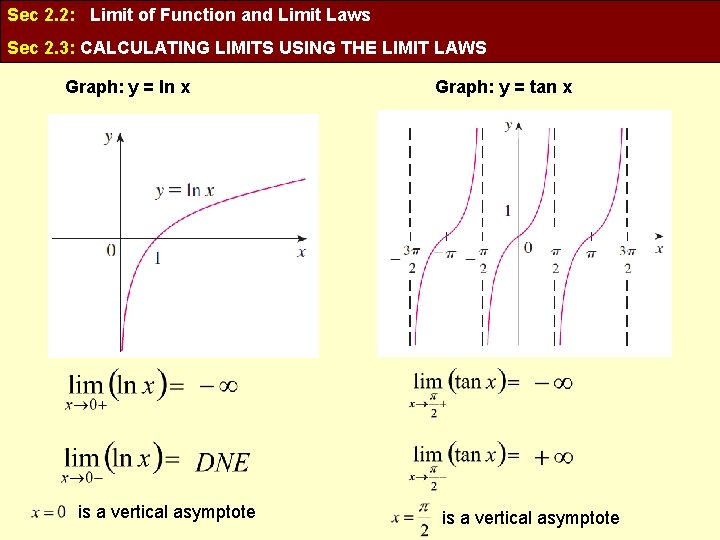
Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS Graph: y = ln x is a vertical asymptote Graph: y = tan x is a vertical asymptote

Sec 2. 2: Limit of Function and Limit Laws Sec 2. 3: CALCULATING LIMITS USING THE LIMIT LAWS
- Slides: 61