Sec 11 3 FiniteDifference Methods for Linear Problems

Sec: 11. 3 Finite-Difference Methods for Linear Problems

Sec: 11. 3 Finite-Difference Methods for Linear Problems The finite difference method for the linear second-order boundary-value problem Example Initial-value problem

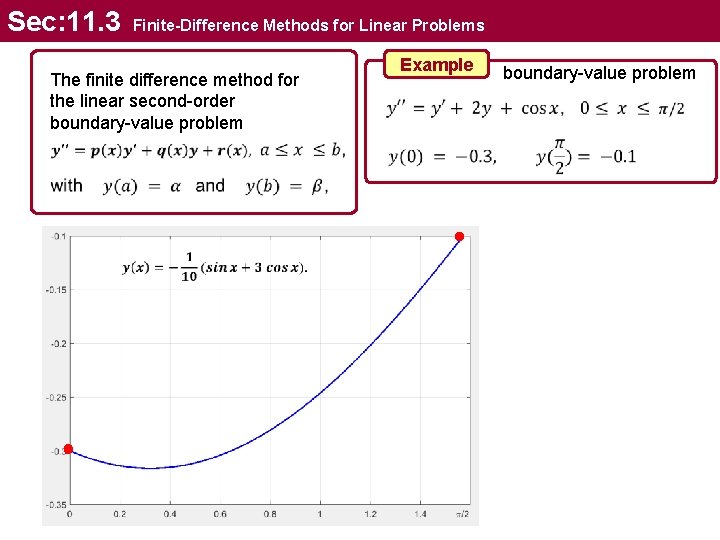
Sec: 11. 3 Finite-Difference Methods for Linear Problems The finite difference method for the linear second-order boundary-value problem Example boundary-value problem

Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem 1 we select an integer N N=3 2 divide the interval [a, b] into (N+1) equal subintervals 3 At the interior mesh points, xi, for i = 1: N, the differential equation is approximated as ( centeral diff )

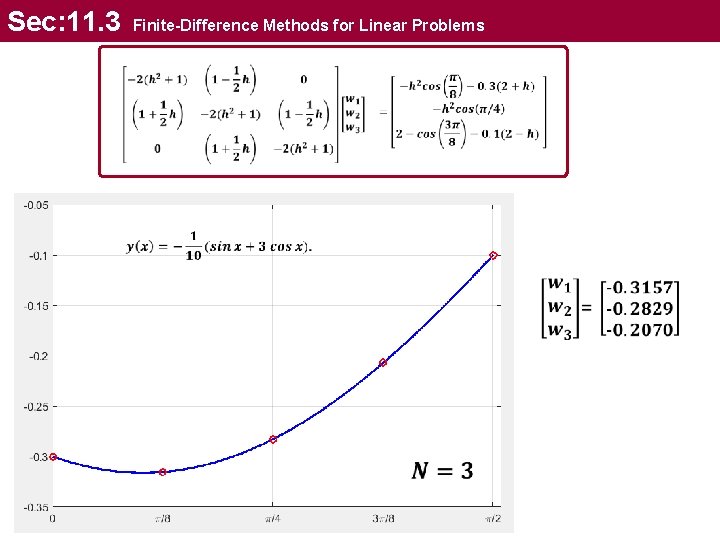
Sec: 11. 3 Finite-Difference Methods for Linear Problems Example We have the following: boundary-value problem 4 5 Write in Matrix form and solve the system

Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem 2. 3084 -0. 8037 0 -1. 1963 2. 3084 -0. 3157 -0. 5014 -0. 1090 -0. 1394 -0. 2829 -0. 2070

Sec: 11. 3 Finite-Difference Methods for Linear Problems

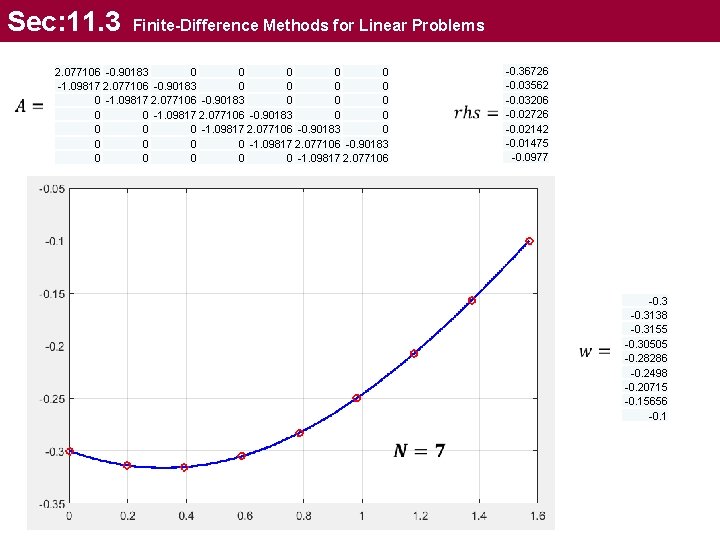
Sec: 11. 3 Finite-Difference Methods for Linear Problems 2. 077106 -0. 90183 0 0 0 0 0 -1. 09817 2. 077106 -0. 36726 -0. 03562 -0. 03206 -0. 02726 -0. 02142 -0. 01475 -0. 0977 -0. 3138 -0. 3155 -0. 30505 -0. 28286 -0. 2498 -0. 20715 -0. 15656 -0. 1

Sec: 11. 3 Finite-Difference Methods for Linear Problems BVP The finite difference method for the linear 2 ed-order BVP

Sec: 11. 3 Finite-Difference Methods for Linear Problems clear; clc a=0; b=pi/2; alpha=-0. 3; beta=-0. 1; p=1; q=2; r = @(x) cos(x); N=3; h=(b-a)/(N+1); x=[a+h: h: b-h]'; d = (2+h^2*q)*ones(N, 1); ad = (-1+h*p/2)*ones(N-1, 1); bd = (-1 -h*p/2)*ones(N-1, 1); A = diag(d) + diag(ad, 1) +diag(bd, -1) rhs = -h^2*r(x); rhs(1) = rhs(1) + alpha*(1+h*p/2); rhs(N) = rhs(N) + beta*(1 -h*p/2); w = Arhs w=[-0. 3 ; w; -0. 1]; x = [0; x ; pi/2]; % ----- display true solution -------y_true = @(x) -(sin(x) + 3*cos(x)). /10; n=100; hh=(b-a)/100; xx=a: hh: b; yt = y_true(xx); plot(xx, yt, '-b', x, w, 'or'); grid on BVP Example

Sec: 11. 3 Finite-Difference Methods for Linear Problems BVP The finite difference method for the linear 2 ed-order BVP Variable Coefficients

Sec: 11. 3 Finite-Difference Methods for Linear Problems Example boundary-value problem 1 we select an integer N N=3 2 divide the interval [a, b] into (N+1) equal subintervals 3 At the interior mesh points, xi, for i = 1: N, the differential equation is approximated as ( centeral diff )

Sec: 11. 3 Finite-Difference Methods for Linear Problems

Sec: 11. 3 Finite-Difference Methods for Linear Problems