Sec 1 5 Measuring Segments Objectives 1 Finding

Sec. 1 – 5 Measuring Segments Objectives: 1) Finding the lengths of segments.
![Geometry vs Algebra �Segments are Congruent �Symbol [ ] �AB CD � 1 2 Geometry vs Algebra �Segments are Congruent �Symbol [ ] �AB CD � 1 2](http://slidetodoc.com/presentation_image_h2/324abe8e4ca03ea150fbc6f9738d9ea6/image-2.jpg)
Geometry vs Algebra �Segments are Congruent �Symbol [ ] �AB CD � 1 2 �Lengths of segments are equal. �Symbol [ = ] �AB = CD �m 1 = m 2 =
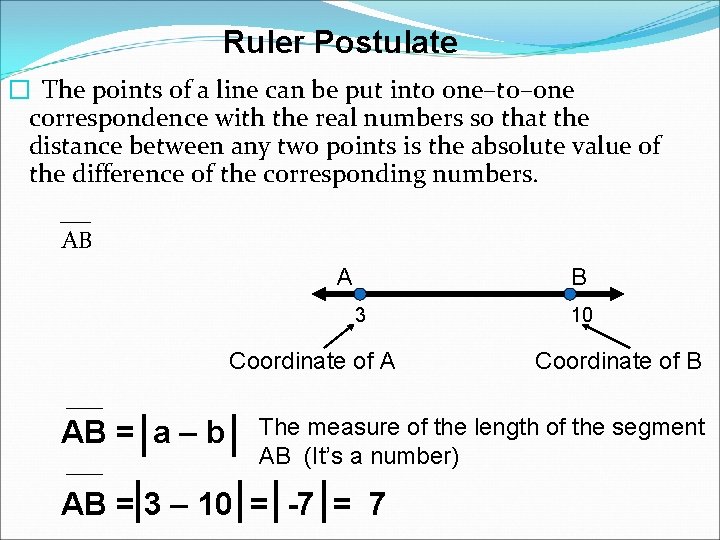
Ruler Postulate � The points of a line can be put into one–to–one correspondence with the real numbers so that the distance between any two points is the absolute value of the difference of the corresponding numbers. AB A B 3 Coordinate of A AB = a – b 10 Coordinate of B The measure of the length of the segment AB (It’s a number) AB = 3 – 10 = -7 = 7

Ex. 1: Find AB, CE, & AC A -8 C -6 B -4 AB = I a – c I AB = -8 – 5 -2 0 2 CE = I c – e I CE = -5 – 6 E 4 6 AB = I a – b I AC = -8 – -5 = -13 = -11 = -8 + 5 = 13 = 11 = -3 = 3 8

Exercise 1: Find which two of the segments XY, ZY, and ZW are congruent. Use the Ruler Postulate to find the length of each segment. XY = | – 5 – (– 1)| = | – 4| = 4 ZY = | 2 – (– 1)| = |3| = 3 ZW = | 2 – 6| = |– 4| = 4 Because XY = ZW, XY ZW.

Segment Addition Postulate �P (1 – 6) If 3 points A, B, & C are collinear & B is between A & C, then AB + BC = AC B A C
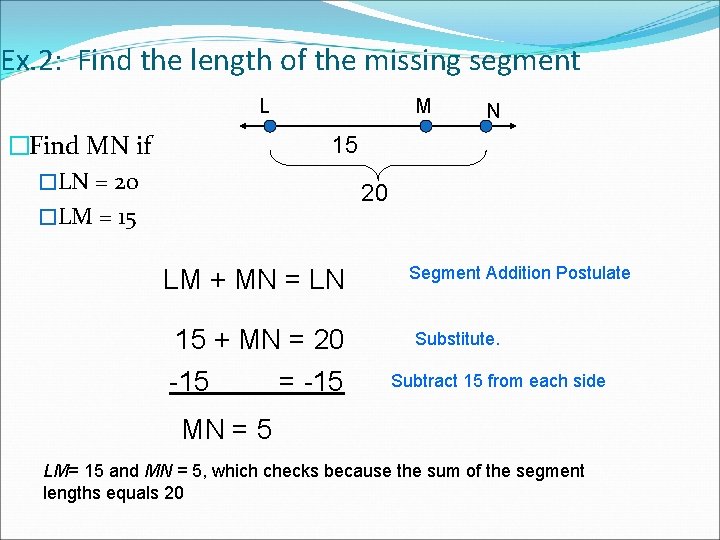
Ex. 2: Find the length of the missing segment L �Find MN if �LN = 20 �LM = 15 M N 15 20 LM + MN = LN 15 + MN = 20 -15 = -15 Segment Addition Postulate Substitute. Subtract 15 from each side MN = 5 LM= 15 and MN = 5, which checks because the sum of the segment lengths equals 20

Ex. 2: Find the length of the missing segment D �Find DS if �DT = 60 �DS = 2 x – 8 �ST = 3 x – 12 DS + ST 2 x - 8 = 80 x = 16 T 3 x - 12 60 = DT (2 x - 8) + (3 x -12) = 60 5 x – 20 = 60 +20 = +20 5 x S Segment Addition Postulate Substitute. Simplify by adding like terms Add 20 from each side Divide each side by 5

�Midpoint – Is a point that divides a segment into two parts. �RS ST �RS = ST R S �Ex. 3: Find AC & CB if C is the Midpoint of AB. �AC = 2 x + 1 �CB = 3 x – 4 A C AC = CB 2 x + 1 = 3 x – 4 T B

What have we learned? ? �Finding the length of segments: D -5 E 0 3 DE = -5 – 3 = 8 Segment Addition: MN + NP = MP (5 x – 4) + (2 x + 14) = 80 7 x + 10 = 80 x = 10 M N 5 x - 4 P 2 x + 14 80
- Slides: 10