Sec 1 4 Segments Rays Parallel Lines and

Sec. 1 – 4 Segments, Rays, Parallel Lines and Planes Objectives: 1) Identify segments and rays. 2) Recognize parallel lines.

Line – A series of points that extend in 2 directions without end. – Notation: 2 capital letters with a line over them. – Ex: AB – Reads: Line AB A B

Segment – Is the part of a line consisting of two endpoints & all the points between them. – Notation: 2 capital letters with a line over them. – Ex: AB – No arrows on the end of a line. – Reads: Line segment (or segment) AB A B

Ray – Is the part of a line consisting of one endpoint & all the points of the line on one side of the endpoint. – Notation: 2 capital letters with a line with an arrow on one end of it. End point always comes first. – Ex: AB – Reads: Ray AB A B

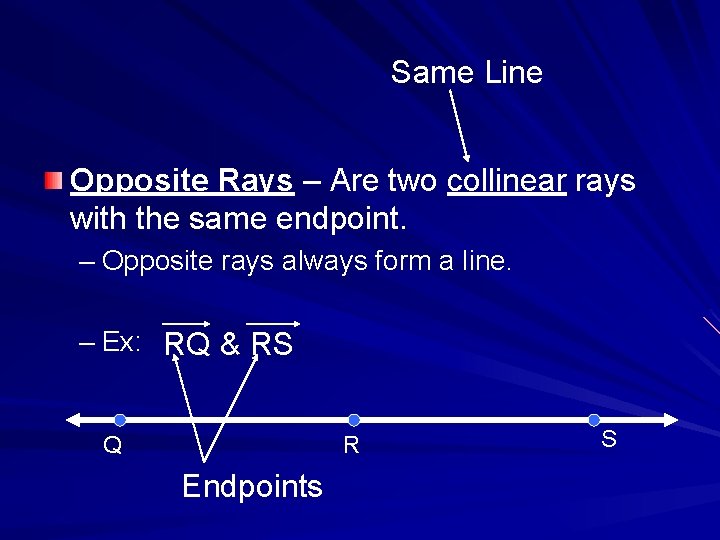
Same Line Opposite Rays – Are two collinear rays with the same endpoint. – Opposite rays always form a line. – Ex: RQ & RS Q R Endpoints S

Ex. 1: Naming segments and rays. L P Name 3 segments: – LP – PQ – LQ Are LP and PL opposite rays? ? No, not the same endpoints Q Name 4 rays: – LQ – QL – PL – LP – PQ

Parallel Lines – Are coplanar lines that never intersect. – Coplanar – same plane – Symbol [ // ] – Ex: r // t – Reads: line r is parallel to line t. r t

Skew Lines – Are noncoplanar lines that never intersect. – Skew lines are never // Parallel Planes – Are planes that do not intersect. E A H D F G B C

What have we learned? ? Name the following line. XY or YZ or ZX Z Name a segment. XY or YZ or XZ Y Name a ray. XY or YZ or ZX or YX X

Use the figure below. Name all segments that are parallel to AE. Name all segments that are skew to AE. Parallel segments lie in the same plane, and the lines that contain them do not intersect. The three segments in the figure above that are parallel to AE are BF, CG, and DH. Skew lines are lines that do not lie in the same plane. The four lines in the figure that do not lie in the same plane as AE are BC, CD, FG, and GH. 1 -3