SEBARAN NEGATIF BINOMIAL r 1 2 3 4

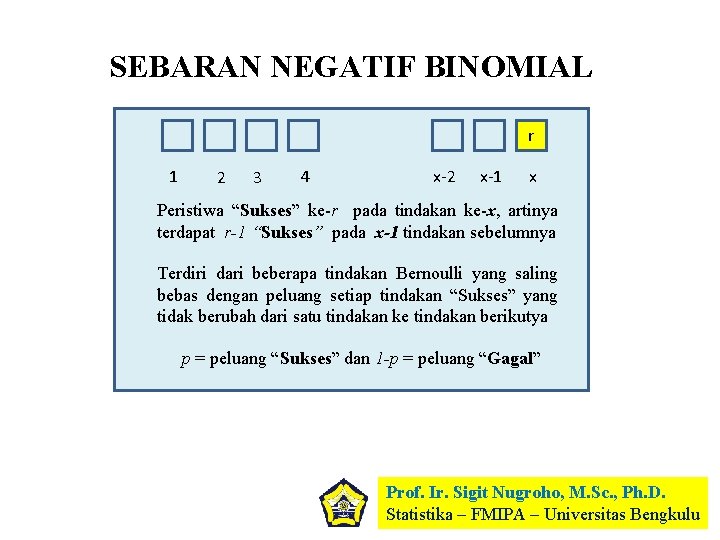
SEBARAN NEGATIF BINOMIAL r 1 2 3 4 x-2 x-1 x Peristiwa “Sukses” ke-r pada tindakan ke-x, artinya terdapat r-1 “Sukses” pada x-1 tindakan sebelumnya Terdiri dari beberapa tindakan Bernoulli yang saling bebas dengan peluang setiap tindakan “Sukses” yang tidak berubah dari satu tindakan ke tindakan berikutya p = peluang “Sukses” dan 1 -p = peluang “Gagal” Prof. Ir. Sigit Nugroho, M. Sc. , Ph. D. Statistika – FMIPA – Universitas Bengkulu

Sebaran Negatif Binomial, juga dikenal sebagai sebaran Pascal atau sebaran Polya, memberikan peluang r-1 peristiwa “Sukses” dan x peristiwa “Gagal” dalam x+r-1 tindakan Bernoulli yang saling bebas dan “Sukses” juga terjadi pada tindakan ke x+r. Nilai x = 0, 1, 2, … Fungsi kepekatan peluang peubah acak nya dapat ditulis Sebaran Negatif Binomial, juga dikenal / dideskripsikan sebagai peristiwa “Sukses” ke-r kalinya pada tindakan ke x. Nilai x = r, r+1, r+2, … fkp nya dapat ditulis Fungsi Pembangkit Momen Sebaran Negatif Binomial

Relasi Koeffisien Binomial Verifikasi Fungsi Kepekatan Peluang Sebaran Negatif Binomial

Fungsi Pembangkit Momen Sebaran Negatif Binomial

Empat momen pertama di sekitar titik pusat Empat momen pertama di sekitar nilai tengah

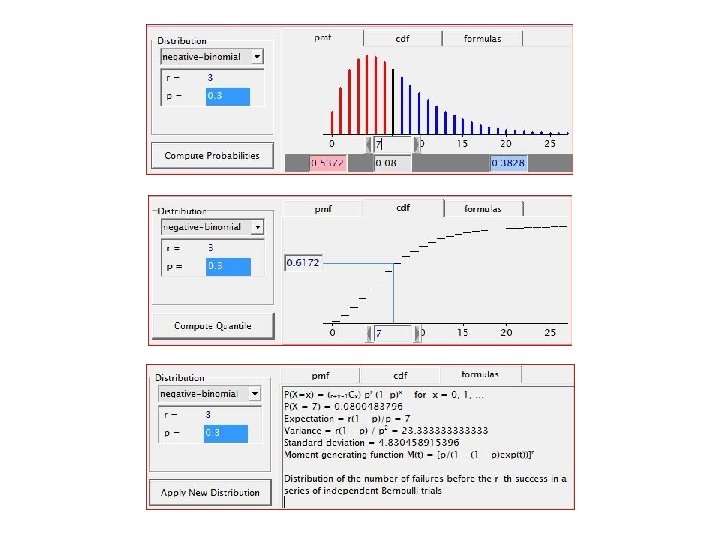
Tugas Kuliah 1. Instalasi militer bawah tanah diperkuat untuk dapat menahan hingga tiga gempuran langsung peluru kendali udara-ke-permukaan tanah. Misalkan pesawat musuh dipersenjatai dengan rudal, masing-masing memiliki peluang 30% mengenai sasaran. Berapa peluang instalasi tersebut akan dapat dihancurkan dengan rudal ketujuh yang ditembakkan? 2. Misalkan X 1, X 2, …, Xk peubah acak yang menyebar dengan sebaran Negatif Binomial berturut dengan parameter berturut-turut r 1 dan p, r 2 dan p, …, rk dan p. Andaikan X = X 1 + X 2 + … + Xk, tentukan MX(t), E(X) dan var(X). 3. Misalkan X 1, X 2, X 3 peubah acak yang menyebar dengan sebaran Negatif Binomial (dibawah ini). Tentukan P(10 X 1+X 2+X 3 12).