Searching and into Trees Trees 1 Searching techniques

Searching (and into Trees) Trees 1

Searching techniques q Searching algorithms in unordered “lists” n n q Searching algorithms in ordered “lists” n n q “Lists” may be arrays or linked lists The algorithms are adaptable to either Primarily arrays with values sorted into order We can exploit the order to search more efficiently Let’s start with arrays n The data held in the array might be w Simple (e. g. numbers, strings) or more complex objects: the search will probably be based on a chosen key field in the objects (e. g. , search student records by registration number) n We will only consider simple data – the searching techniques are the same Trees 2

Sequential search in an unordered list q In these algorithms we will assume: n n n q The basic technique to be used is “sequential search” n q The data is integers Held in an array variable numbers, Is in random order The number of data values is indicated by a variable size The data is in elements indexed 0 to (size-1) We are seeking the integer held in variable val Compare val with the value in numbers[0], then with that in numbers[1], etc We will look at two versions of an algorithm encoding this n Other adaptations are possible Trees 3

Algorithm 1: Standard sequential search q q Here is a basic search algorithm. It leaves its result in a variable called position: wint position = 0; while (position < size) { if (numbers[position] == val) break; // Exit loop if found position++; } If val is not present: n The entire array will be scanned - taking size steps n position will have a final value of size But if val is present: n break; -> the while loop terminates immediately n The average number of scanning steps expected is size/2 Easy to adapt to return a boolean, or throw an exception Trees 4

q If we are careful, we can combine the loop test and the array element check: n n n int position = 0; while (numbers[position] != val && position < size) position++; Is this correct? int position = 0; while (numbers[position++] != val && position < size); Trees 5

Corrected Version q If we are careful, we can combine the loop test and the array element check: int position = 0; while (position < size && numbers[position] != val) position++; 1. 2. 3. 4. The && test checks position < size first, and if it is false does not check numbers[position] != val otherwise would get Array. Index. Out. Of. Bounds. Exception if val is not present! This is called "conditional" or "short-circuit" behaviour: it applies to && and || Trees 6

Algorithm 2: Sequential search with a “sentinel” q We can improve the basic search algorithm if the array numbers has one extra element, numbers[size], that is never used for actual data n n Instead we place a copy of the sought value there, so the search always succeeds. This means that the loop does not need to carry out the “end of array” test - less work, so quicker. int[] numbers = new int[size+1]; . . . int position = 0; numbers[size] = -1; // Insert "sentinel" while (numbers[position] != val) position++; return position; As before, position has the final value size if val is not present Trees 7

q q We may be interested in an algorithm’s best case, worst case or average execution time: For the sequential search algorithm (with or without sentinel): n n n Best case is 1 step: O(1) Worst case is N steps: O(N) The actual average number of steps depends on ratio of successful/unsuccessful searches: The average of successful searches is N/2 steps, and so is O(N) All unsuccessful searches take N steps, which is O(N), So overall the average complexity is O(N) Trees 8

Searching an Ordered List q Again we will assume: n n q q The data is integers, held in an array sequence, So the data is in elements indexed 0 to (length-1) But this time we assume that the values are held in ascending numerical order We are seeking the integer held in val We could use the sequential search algorithm, but this does not take advantage of the knowledge that the data is ordered. (The complexity remains O(N). ) Instead, we will take advantage of the ordering to improve search efficiency (i. e. , to reduce the complexity) Trees 9

Binary Search q q q If the data is already ordered, we can do much better than a linear time algorithm. Here is the scheme: n Pick the middle element in the array n If it is equal to val, stop the search n If it is greater than val, search the lower half of the remaining array n If it is less than val, search the remaining upper half At each iteration: n We are searching in a remaining partition of the array n We cut the remaining partition in half, rather than just removing one element Example: Searching for 11 in w 1, 3, 5, 7, 9, 11, 13 n First compare with 7, so search in 9, 11, 13 n Now compare with 11 - found it - in two steps Trees 10

q Concretely: n n Let variable low indicate the lowest element of the partition (index 0 initially) high (h) indicate the highest element (size-1 initially) middle (m) indicate the next element being tested The search for 11 proceeds like this: low=0 h=6 m=3 0 1 2 3 4 1 3 5 7 9 low Not found, and 11>7, so low=(m+1)=4 h=6 1 5 11 13 h m 3 5 7 m=5 6 9 11 13 low m h Found it, at index 5 Trees 11

An unsuccessful search: search for 10 0 low=0 h=6 m=3 Not found, and 10>7, so low=(m+1)=4 h=6 1 2 3 4 1 3 low 5 7 m 9 11 13 h 5 7 9 11 13 1 3 m=5 low m Not found, and 10<11, so 1 low=4 h=(m-1)=4 3 5 7 m=4 Not found, and 10>9, so low=(m+1)=5 h=4 5 9 6 h 11 13 low h m 1 3 5 7 9 11 13 h low Now low>h, and the partition has Trees “vanished”: the search has failed 12

q Algorithm binary. Search: INPUT: val – value of interest, sequence – sorted data OUTPUT: object or value of interest if exists, null otherwise int low = 0, middle = 0, high = seq. length; while (high >= low) { middle = (high + low) / 2; if (sequence[middle] == val) return sequence[middle]; // Found it else if (sequence[middle] < val) low = middle + 1; // Search upper half else high = middle - 1; // Search lower half } return -1; // or null if an object-type q The outcomes: n Ordinary loop exit when the indexes “cross” not found (i. e. high < low) n Loop exit on return found (detect this by testing high >= low) Trees 13

The Complexity of Binary Search q q q Best case: val is exactly sequence[middle] at the first step N 1 n The search stops after first step, so complexity O(1) 2 4 8 Worst case: 16 32 n This will be when we continue dividing until the “partition” 64 contains only one value: then it is either equal to val or not 128 256 n For 250 elements this turns out to be about 8 iterations 512 1024 n For 500 it is about 9 2048 4096 8192 n For 1000 it is about 10 16384 32768 n Double the amount of data Add one step! 65536 steps 131072 n In general: the size is approximately 2 262144 524288 n So the number of steps is approximately log 2 size 1048576 n Complexity is O(log. N) n For emphasis: double the amount of data Add one step! Average case: n Don’t need to consider this: the worst case is very good! Trees 14 log 2 N 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

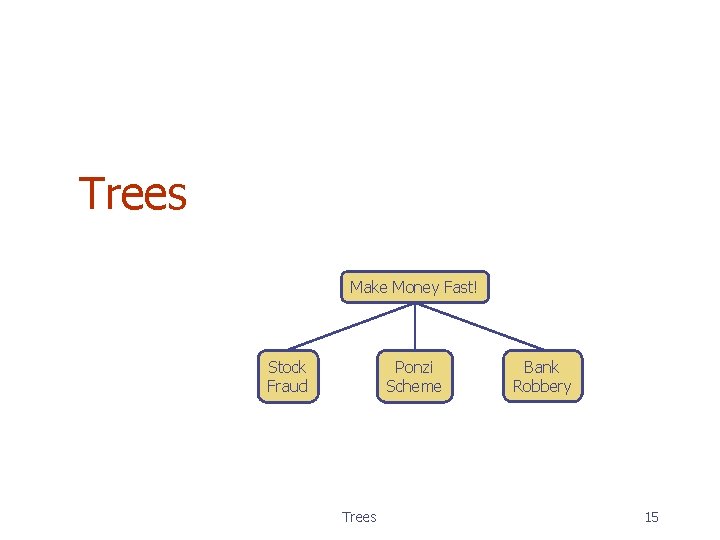
Trees Make Money Fast! Stock Fraud Ponzi Scheme Trees Bank Robbery 15

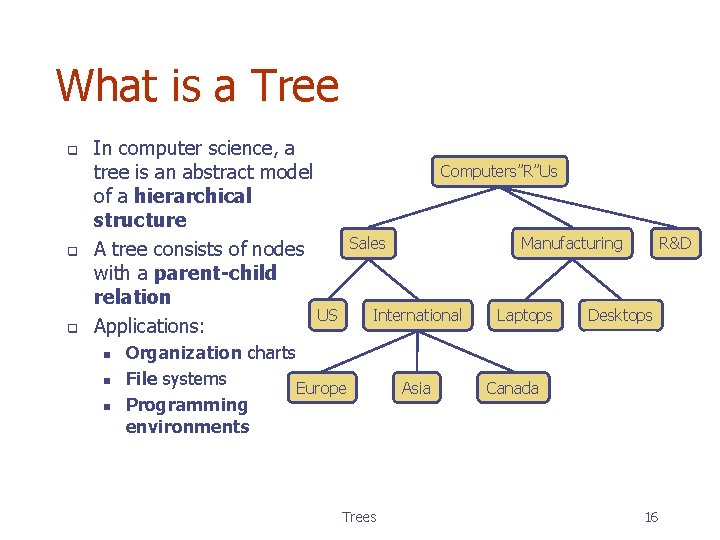
What is a Tree q q q In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes with a parent-child relation US Applications: n n n Computers”R”Us Sales Manufacturing International Organization charts File systems Europe Programming environments Trees Asia Laptops R&D Desktops Canada 16

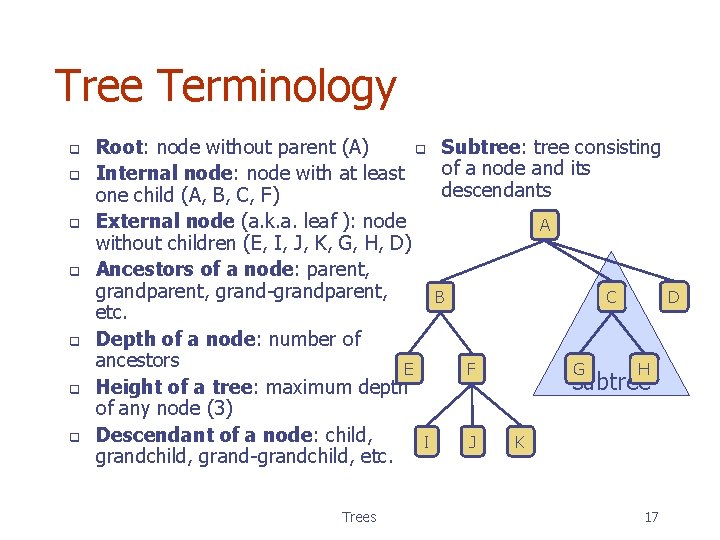
Tree Terminology q q q q Root: node without parent (A) q Subtree: tree consisting of a node and its Internal node: node with at least descendants one child (A, B, C, F) External node (a. k. a. leaf ): node A without children (E, I, J, K, G, H, D) Ancestors of a node: parent, grand-grandparent, B C etc. Depth of a node: number of ancestors E F G H subtree Height of a tree: maximum depth of any node (3) Descendant of a node: child, I K J grandchild, grand-grandchild, etc. Trees 17 D

Tree ADT q q We use positions to abstract nodes Generic methods: n n q integer size() boolean is. Empty() Iterator iterator() Iterable positions() n n n boolean is. Internal(p) boolean is. External(p) boolean is. Root(p) Update method: n element replace (p, o) Additional update methods may be defined by data structures implementing the Tree ADT Accessor methods: n Query methods: position root() position parent(p) Iterable children(p) Trees 18

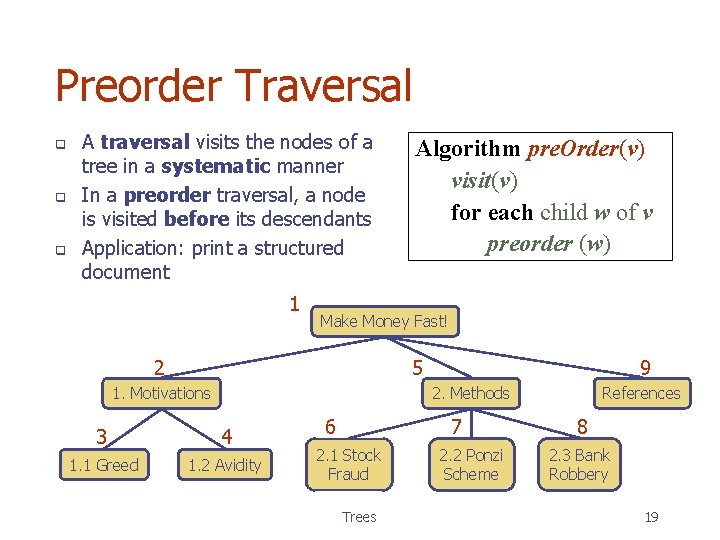
Preorder Traversal q q q A traversal visits the nodes of a tree in a systematic manner In a preorder traversal, a node is visited before its descendants Application: print a structured document 1 Algorithm pre. Order(v) visit(v) for each child w of v preorder (w) Make Money Fast! 2 5 1. Motivations 9 2. Methods 3 4 1. 1 Greed 1. 2 Avidity 6 7 2. 1 Stock Fraud Trees 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery 19

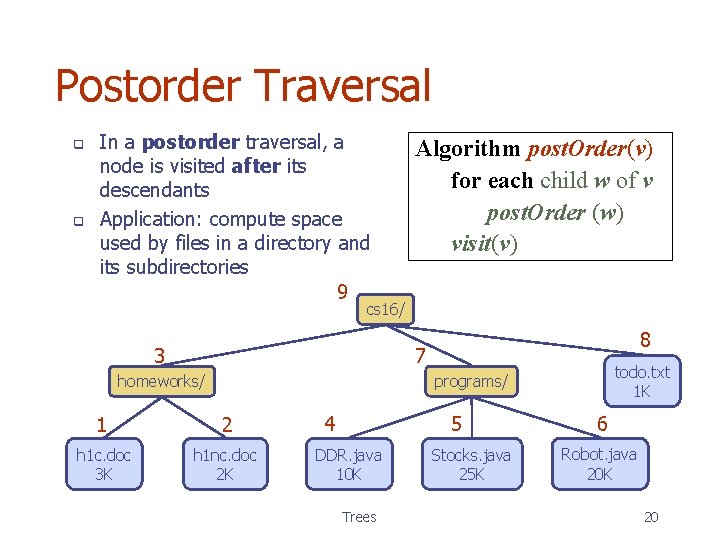
Postorder Traversal q q In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 8 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K 4 5 DDR. java 10 K Trees Stocks. java 25 K 6 Robot. java 20 K 20

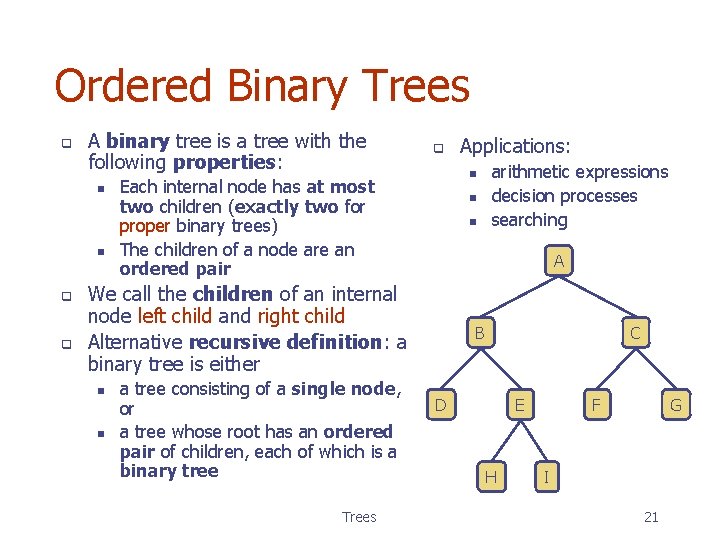
Ordered Binary Trees q A binary tree is a tree with the following properties: n n q q q n Each internal node has at most two children (exactly two for proper binary trees) The children of a node are an ordered pair n n n a tree consisting of a single node, or a tree whose root has an ordered pair of children, each of which is a binary tree Trees arithmetic expressions decision processes searching A We call the children of an internal node left child and right child Alternative recursive definition: a binary tree is either n Applications: B C D F E H G I 21

Arithmetic Expression Tree q Binary tree associated with an arithmetic expression n n q internal nodes: operators external nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a 3 b 1 Trees 22

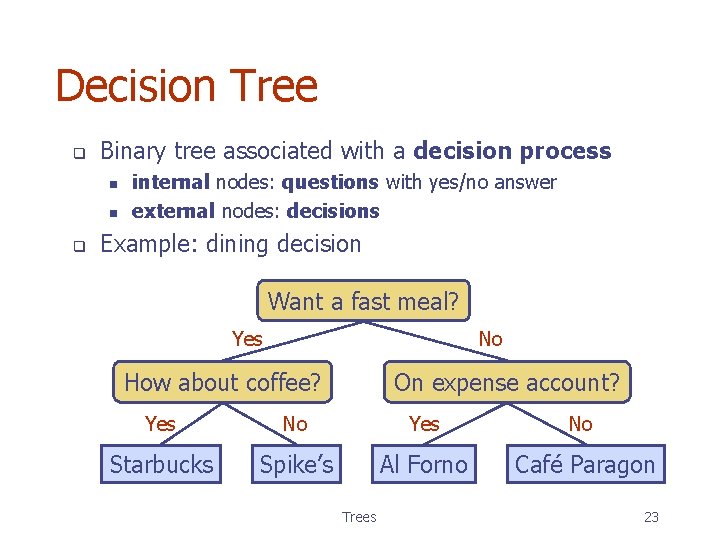
Decision Tree q Binary tree associated with a decision process n n q internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon Trees 23

Binary. Tree ADT q q The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT Additional methods: n n position left(p) position right(p) boolean has. Left(p) boolean has. Right(p)Trees q Update methods may be defined by data structures implementing the Binary. Tree ADT 25

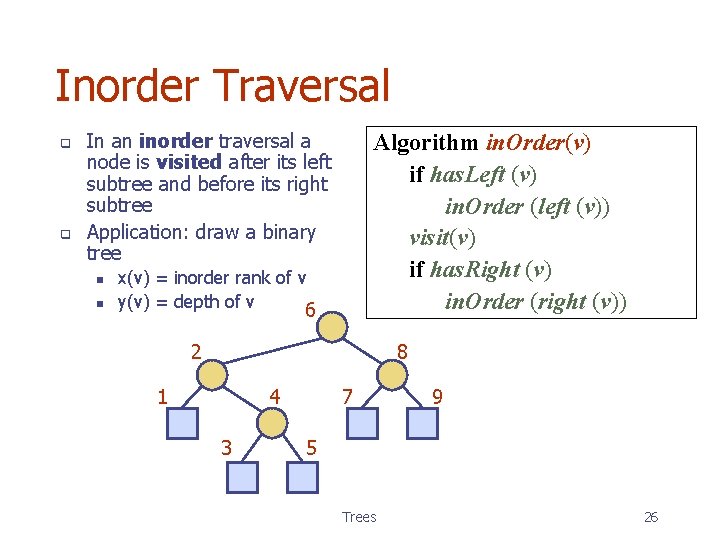
Inorder Traversal q q In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree n n Algorithm in. Order(v) if has. Left (v) in. Order (left (v)) visit(v) if has. Right (v) in. Order (right (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 7 9 5 Trees 26

Print Arithmetic Expressions q Specialization of an inorder traversal n n n print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 3 Algorithm print. Expression(v) if has. Left (v) print(“(’’) in. Order (left(v)) print(v. element ()) if has. Right (v) in. Order (right(v)) print (“)’’) b ((2 (a - 1)) + (3 b)) 1 Trees 27

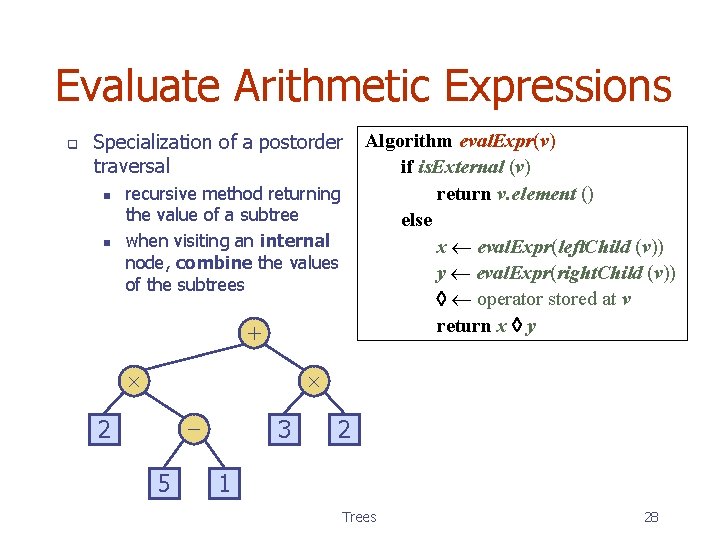
Evaluate Arithmetic Expressions q Specialization of a postorder traversal n n recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees + Algorithm eval. Expr(v) if is. External (v) return v. element () else x eval. Expr(left. Child (v)) y eval. Expr(right. Child (v)) operator stored at v return x y - 2 5 3 2 1 Trees 28

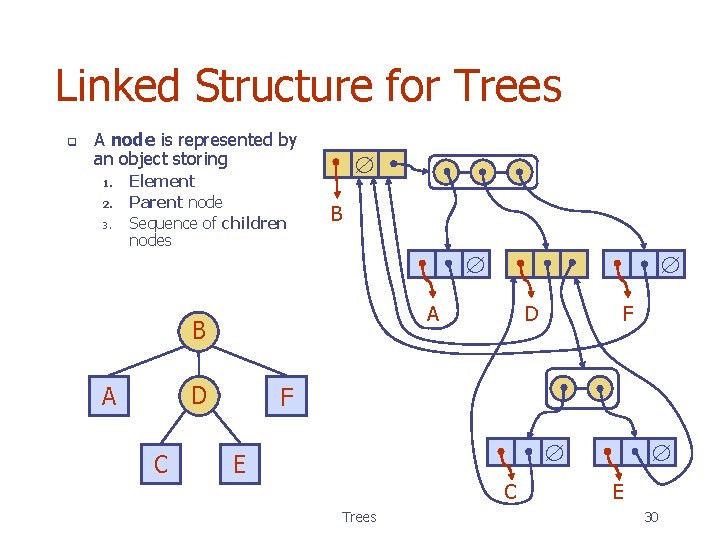
Linked Structure for Trees q A node is represented by an object storing 1. 2. 3. Element Parent node Sequence of children nodes B A B D A C D F F E C Trees E 30

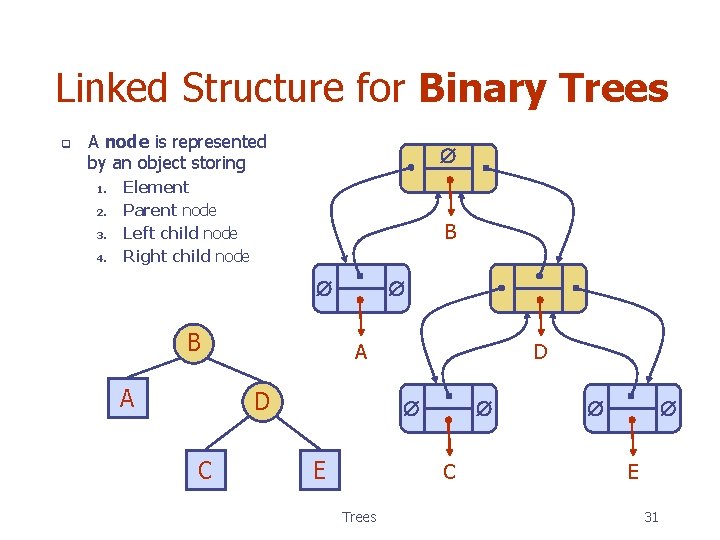
Linked Structure for Binary Trees q A node is represented by an object storing 1. 2. 3. 4. Element Parent node Left child node Right child node B B A A D C D E C Trees E 31

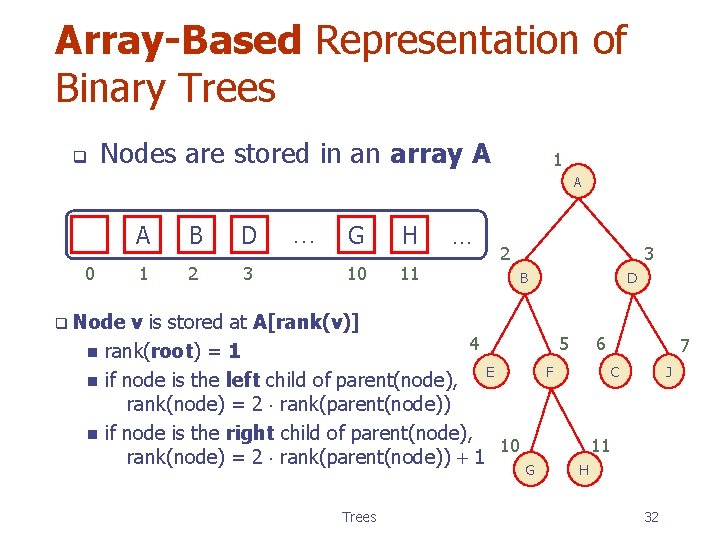
Array-Based Representation of Binary Trees q Nodes are stored in an array A 1 A 0 A B D 1 2 3 … G H 10 11 … 2 B D q Node n n n v is stored at A[rank(v)] 4 rank(root) = 1 E if node is the left child of parent(node), rank(node) = 2 rank(parent(node)) if node is the right child of parent(node), 10 rank(node) = 2 rank(parent(node)) + 1 3 Trees 5 6 7 C F J 11 G H 32