SearchBased Inference of Polynomial Metamorphic Relations By Jie

Search-Based Inference of Polynomial Metamorphic Relations By: Jie Zhang Peking University, China zhangjie 12@sei. pku. edu. cn

Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work
Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work
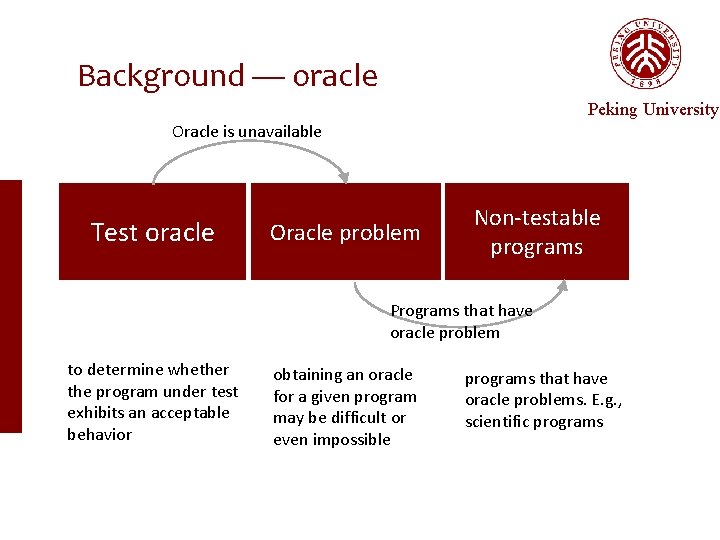
Background — oracle Peking University Oracle is unavailable Test oracle Oracle problem Non-testable programs Programs that have oracle problem to determine whether the program under test exhibits an acceptable behavior obtaining an oracle for a given program may be difficult or even impossible programs that have oracle problems. E. g. , scientific programs

Non-testable programs How to solve the oracle problem and test the nontestable programs?

Non-testable programs How to solve the oracle problem and test the nontestable programs?
Non-testable programs How to solve the oracle problem and test the nontestable programs? A possible solution: find some pseudo oracles

Non-testable programs How to solve the oracle problem and test the nontestable programs? A possible solution: find some pseudo oracles Metamorphic relations

Metamorphic relations Peking University Typically, an MR specifies how a particular change to the input would change the output

Metamorphic relations Peking University Typically, an MR specifies how a particular change to the input would change the output

Metamorphic relations Peking University

Metamorphic relations Peking University

Metamorphic relations Peking University

Metamorphic relations Peking University

Metamorphic relations Peking University

Metamorphic relations Peking University Metamorphi c Testing

Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work

Motivation Peking University • Testers often lack of thorough knowledge of the PUT: • In many circumstances, it’s difficult to manually acquire MRs • can be regarded as program invariants. Very important in helping understand the program under test • more MRs: help achieve more adequate testing

Motivation Peking University • Testers often lack of thorough knowledge of the PUT: • In many circumstances, it’s difficult to manually acquire MRs • can be regarded as program invariants. Very important in helping understand the program under test • more MRs: help achieve more adequate testing

Motivation Peking University • Testers often lack of thorough knowledge of the PUT: • can be regarded as program invariants. Very important in helping understand the program under test Our work: automatically infer MRs for • In many circumstances, • more MRs: help programs under test it’s difficult to achieve more manually acquire MRs adequate testing

Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work
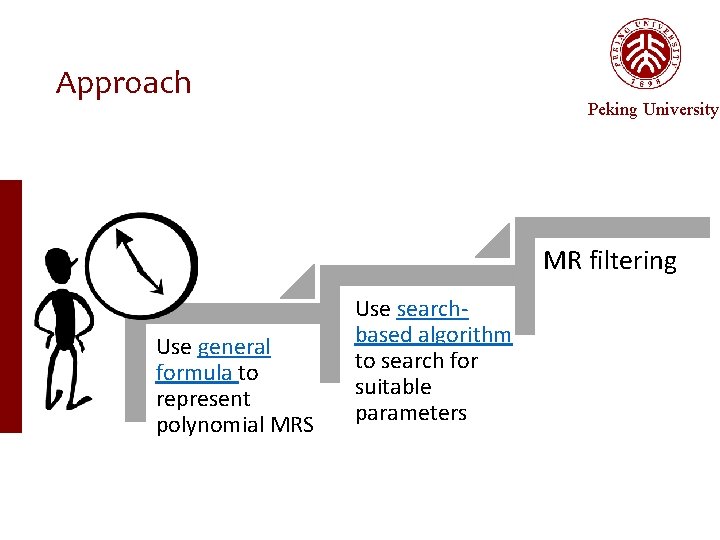
Approach Peking University MR filtering Use general formula to represent polynomial MRS Use searchbased algorithm to search for suitable parameters
Approach Peking University MR filtering Use general formula to represent polynomial MRS Use searchbased algorithm to search for suitable parameters

Metamorphic Relations Peking University 60% 50%

Metamorphic Relations Peking University 1 -MR 60% 50% 2 -MR

Peking University 1 -MR

Peking University 1 -MR

Peking University 1 -MR 2 -MR
Peking University Infer MRs Find polynomial equations
Peking University Infer MRs Find polynomial equations Search problem
Peking University Infer MRs Find polynomial equations Search problem First step second step
Approach Peking University MR filtering Use general formula to represent polynomial MRS Use searchbased algorithm to search for suitable parameters

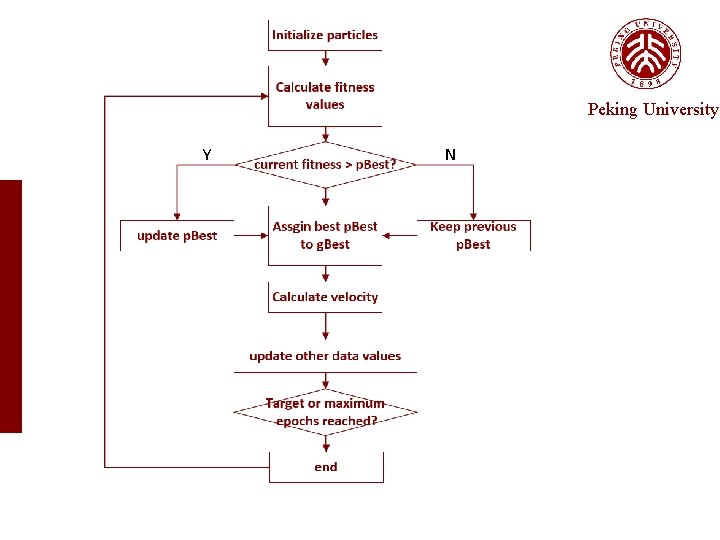
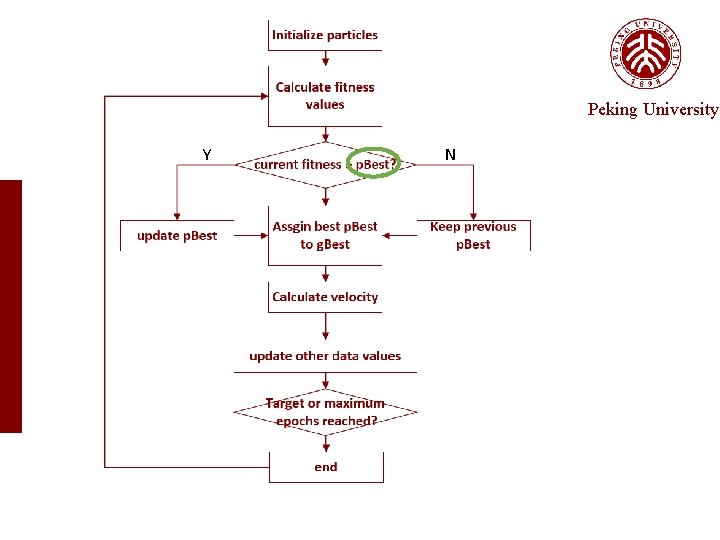
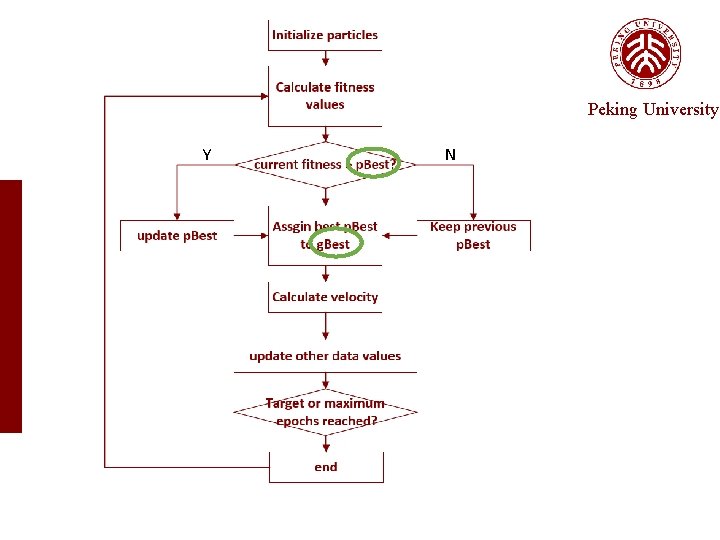
Approach — search-based algorithm Peking University • PSO algorithm: PSO algorithm (Particle Swarm Optimization) simulating the birds foraging behavior. • each candidate solution is called a particle • Each particle has a velocity and a location which keep changing • A fitness function is used to evaluate how close the location of a particle is to an optimal location • Why PSO : • very effective to search in continuous space • can lead a particle to escape local optimal locations. • Simple, no many parameters to adjust
Peking University Y N
Peking University Y N
Peking University Y N

Fitness function The vector of parameters Peking University The k-th input • If L and the k-th input satisfy the general formula, we define f(L, k) = 1, otherwise we define f(L, k) = 0. The fitness function: actually counts the number of inputs that satisfy the general formula.

Process Peking University a. In the beginning, the N particles are assigned with locations (initial values of the parameters). b. The N particles keep updating their velocities and locations according to p. Best and g. Best. c. When reaching the termination threshold, over. The global optimum location that any particle has ever reached is returned as the final solution.
Approach Peking University MR filtering Use general formula to represent polynomial MRs Use searchbased algorithm to search for suitable parameters

MR Filtering Peking University •
Approach I’ve got highquality MRs automatically and timely Peking University s MR MR filtering Use general formula to represent polynomial MRS Use searchbased algorithm to search for suitable parameters
Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work
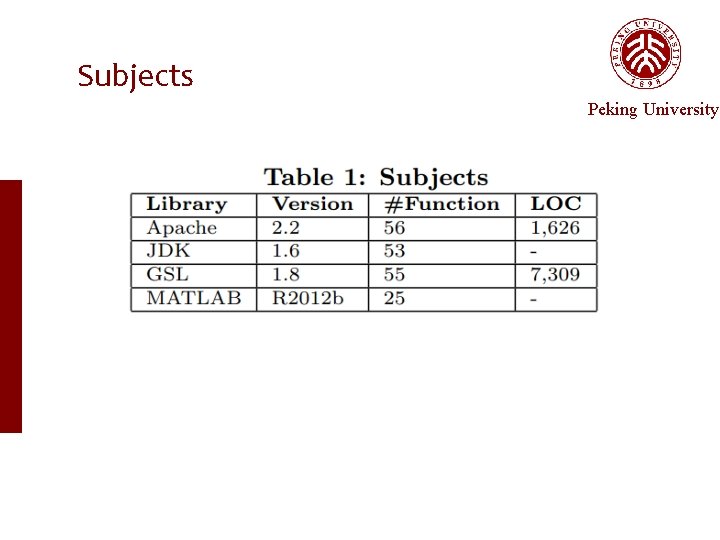
Subjects Peking University
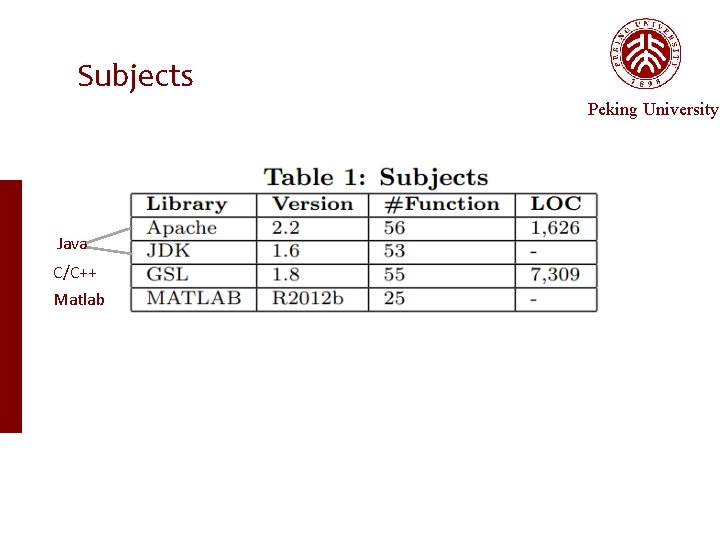
Subjects Peking University Java C/C++ Matlab
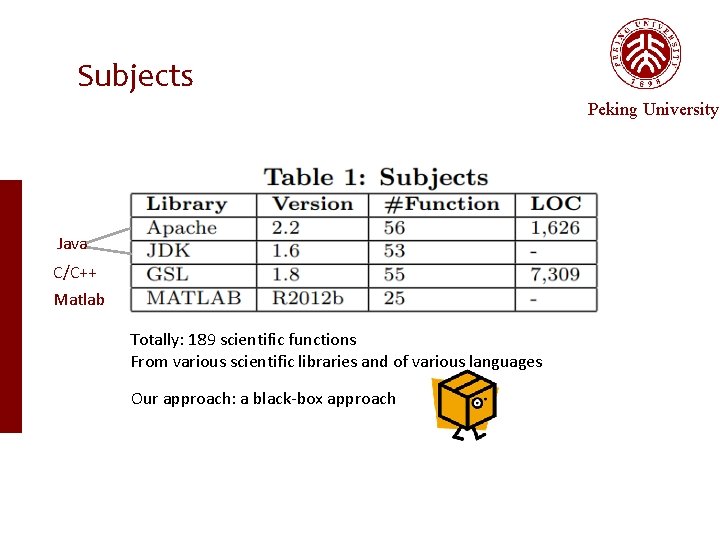
Subjects Peking University Java C/C++ Matlab Totally: 189 scientific functions From various scientific libraries and of various languages Our approach: a black-box approach
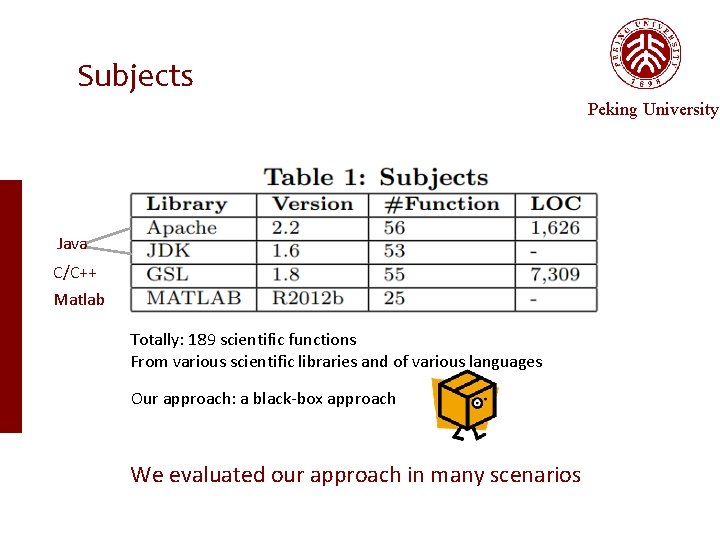
Subjects Peking University Java C/C++ Matlab Totally: 189 scientific functions From various scientific libraries and of various languages Our approach: a black-box approach We evaluated our approach in many scenarios
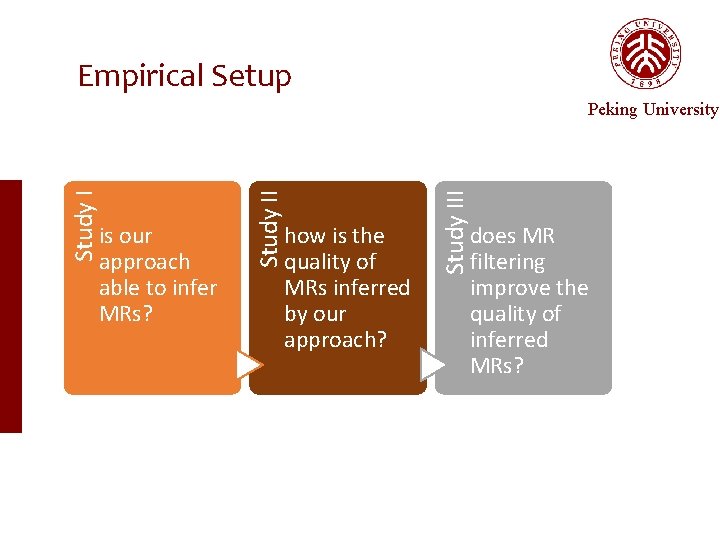
Empirical Setup how is the quality of MRs inferred by our approach? Study III is our approach able to infer MRs? Study II Study I Peking University does MR filtering improve the quality of inferred MRs?

Empirical Setup — study. I Study I Peking University is our approach able to infer MRs? Run our three-step approach on our subjects Record the results and the time
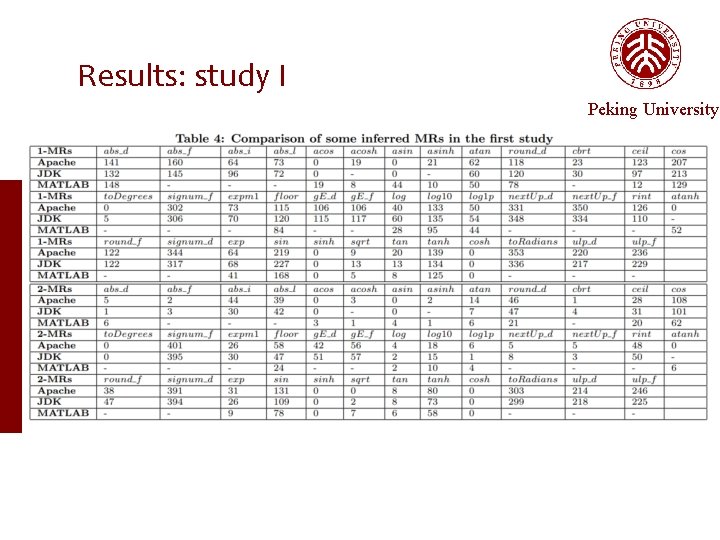
Results: study I Peking University
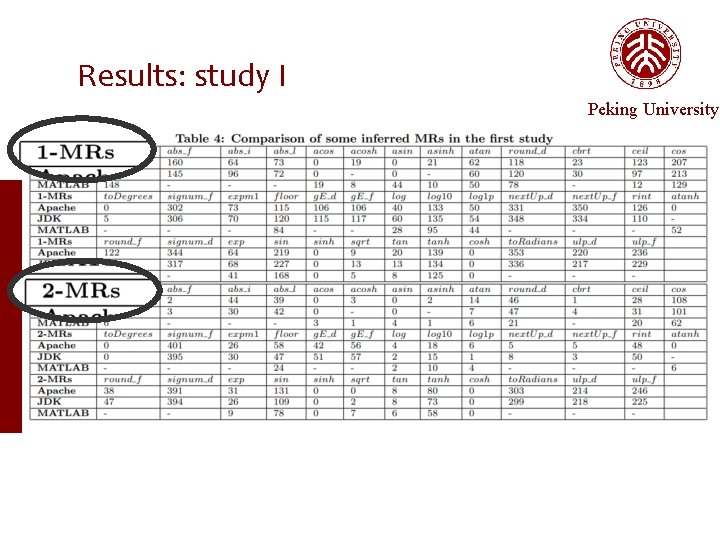
Results: study I Peking University
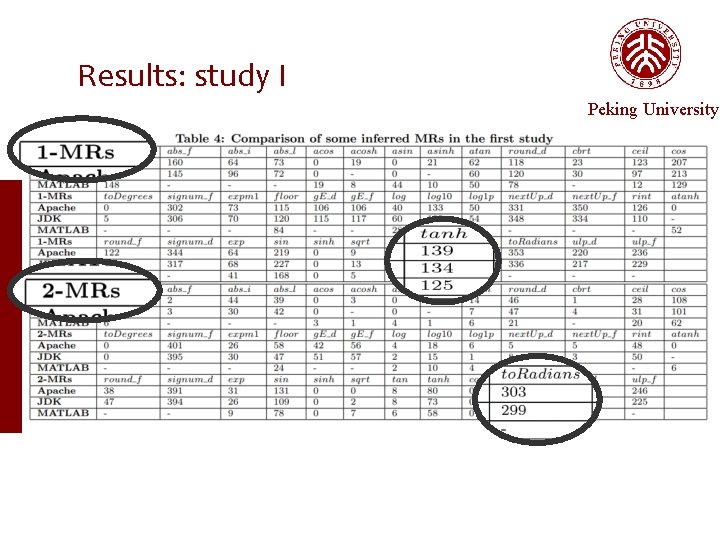
Results: study I Peking University

Some Typical MRs Peking University • ……

Some Surprising MRs Peking University ……

Empirical Setup — study II Study II Peking University how is the quality of MRs inferred by our approach?

Empirical Setup — study II Peking University Study II • For simple functions: manually check the quality how is the quality of MRs inferred by our approach?

Empirical Setup — study II Study II Peking University how is the quality of MRs inferred by our approach? • For simple functions: manually check the quality • Compare the number of MRs inferred from different libraries

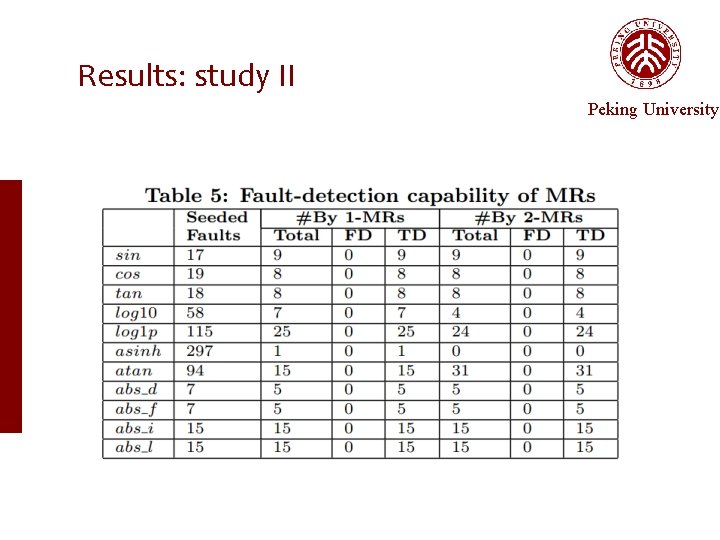
Empirical Setup — study II Study II Peking University how is the quality of MRs inferred by our approach? • For simple functions: manually check the quality • Compare the number of MRs inferred from different libraries • Investigate the fault-detection capability of inferred MRs

Empirical Setup — study II Study II Peking University how is the quality of MRs inferred by our approach? • For simple functions: manually check the quality • Compare the number of MRs inferred from different libraries • Investigate the fault-detection capability of inferred MRs ü Simulate the regression testing in software evolution ü Apply the MRs inferred from the correct version on detecting faults in the subsequent version ü Faults construction: use mutation tools to generate mutants only in the changed lines

Results: study II Peking University
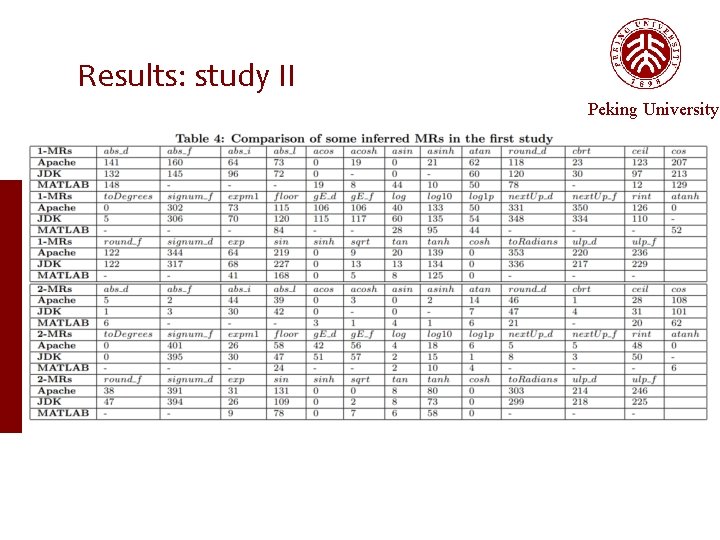
Results: study II Peking University
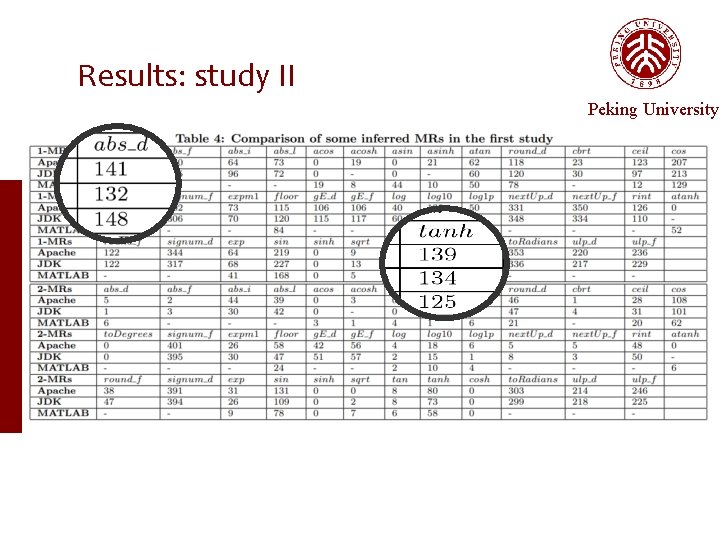
Results: study II Peking University
Results: study II Peking University

Empirical Setup — study III Study III Peking University does MR filtering improve the quality of the inferred MRs? Compare the quality of MRs inferred with MR filtering and without MR filtering (true detections and false detections) V S
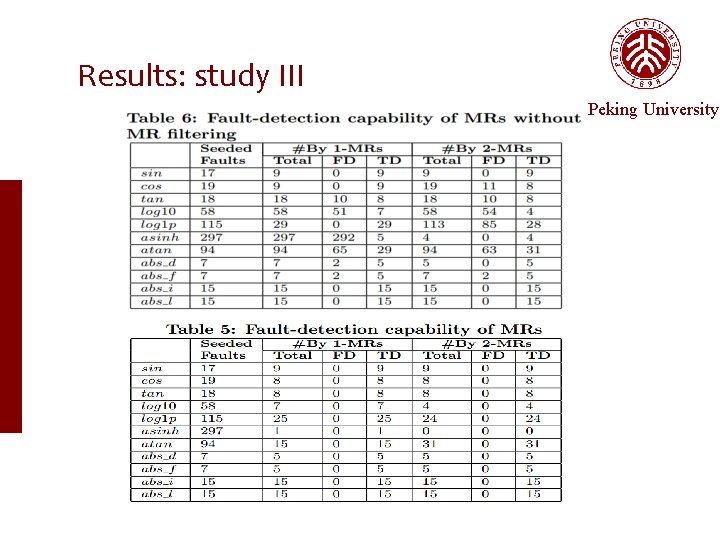
Results: study III Peking University
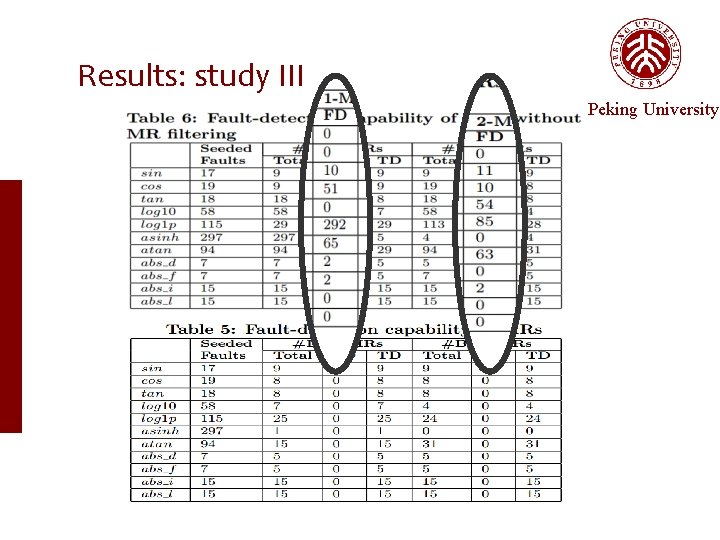
Results: study III Peking University
Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work

Summary Peking University • We propose a novel approach to automatically inferring polynomial metamorphic relations • We view the problem of MR inference as a searching problem and thus use a typical optimization algorithm PSO to solve the problem. • We conducted three empirical studies and got the finding that our approach is able to infer many MRs with high quality in acceptable time, which are effective in detecting faults with no false detection.
Outline Peking University 2. motivation 1. background 4. Empirical setup 6. Summary 3. approach 5. results 7. Future work
Future Work Peking University
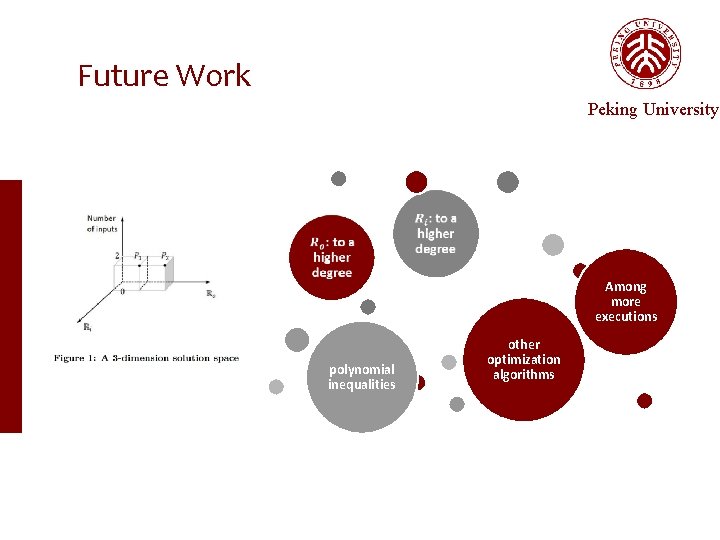
Future Work Peking University Among more executions polynomial inequalities other optimization algorithms

Q & A
- Slides: 71