SE 435 Distributed Systems Marshalling Background Principles Version

SE 435 – Distributed Systems Marshalling – Background Principles Version 2. 0 Clark Elliott De. Paul University

Preliminary slides cut from excellent materials at: http: //www. cs. wpi. edu/~fcco/classes/cs 45152005/lectures/cs 4515 -06. ppt By Fernando C. Colon Osorio Augmented by Elliott

Some Essential Background Principles q q q q q From transistors to memory Binary Arithmetic Designing the ALU – arithmetic and logic not just arithmetic From bit strings to architectures Process Memory is only on loan Processes, context switching, symbol tables Marshalling Summaries

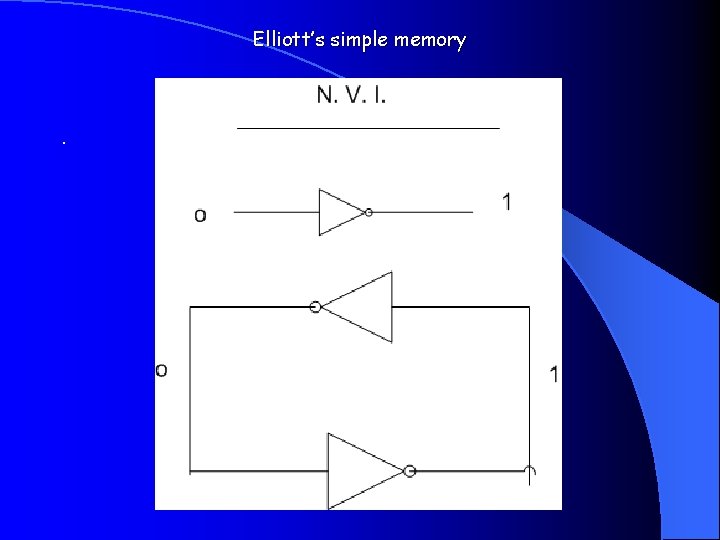
Elliott’s simple memory .

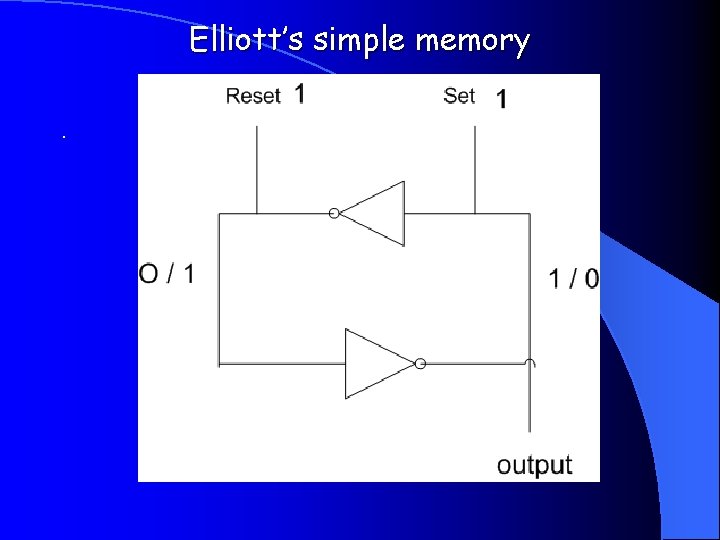
Elliott’s simple memory.

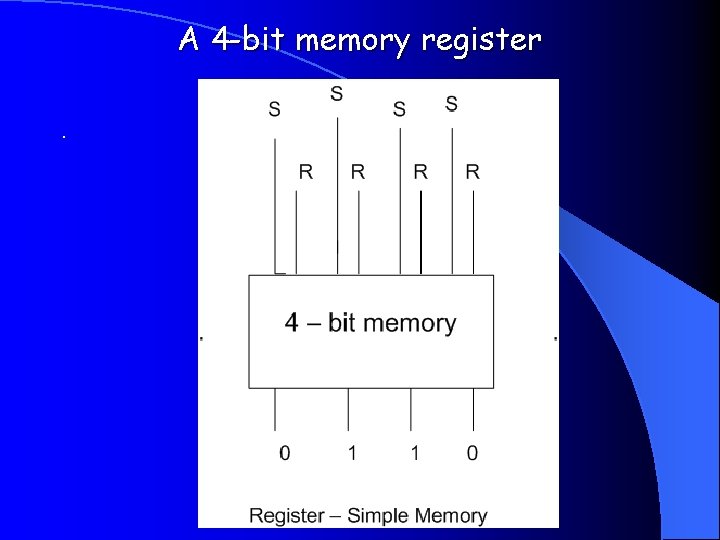
A 4 -bit memory register.

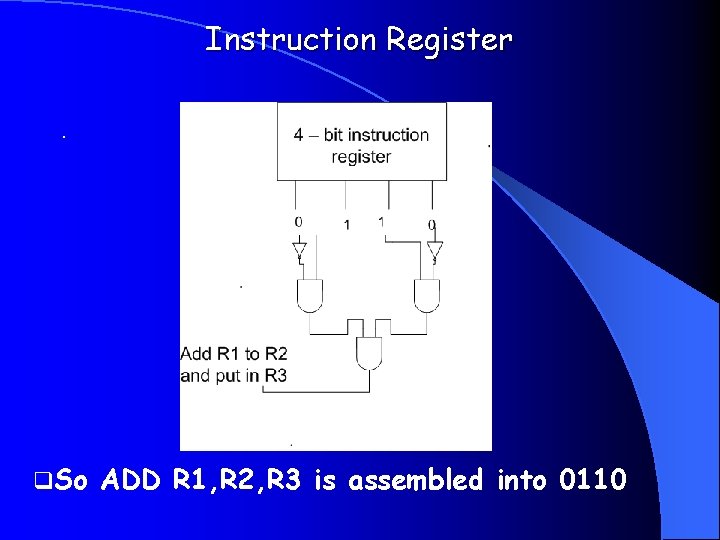
Instruction Register. q. So ADD R 1, R 2, R 3 is assembled into 0110

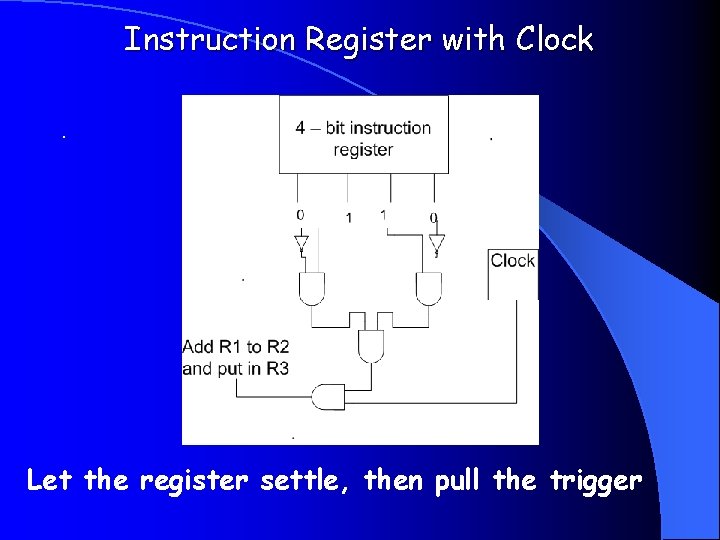
Instruction Register with Clock. Let the register settle, then pull the trigger

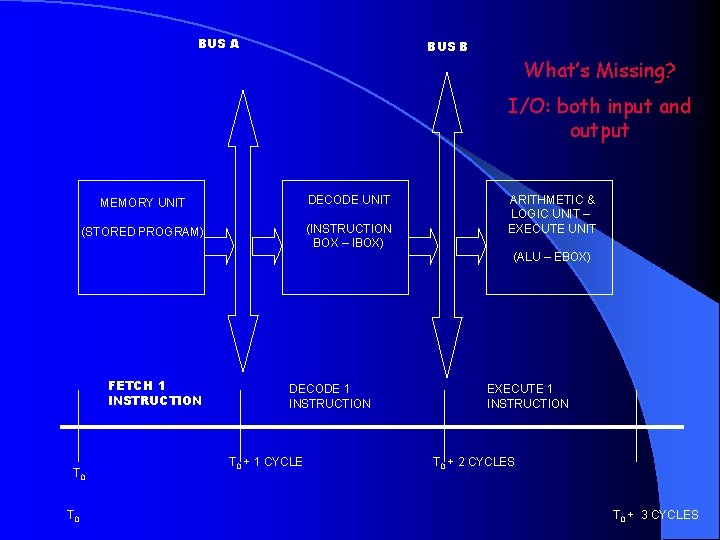
BUS A BUS B What’s Missing? I/O: both input and output MEMORY UNIT DECODE UNIT (STORED PROGRAM) (INSTRUCTION BOX – IBOX) ARITHMETIC & LOGIC UNIT – EXECUTE UNIT (ALU – EBOX) FETCH 1 INSTRUCTION T 0 DECODE 1 INSTRUCTION T 0 + 1 CYCLE EXECUTE 1 INSTRUCTION T 0 + 2 CYCLES T 0 + 3 CYCLES

Symbolic Values Bits are just bits -- they have no inherent meaning q Conventions define relationship between bits and numbers, bits and characters, etc. q q q q 1010 could one. 1010 could mean one eight and one two. mean one two, but it is negative mean zero eights, one four, zero twos, and mean the letter “a” mean… That is, until we lay some interpretation over a string of bits they have no value to us.

Numbers q Binary numbers (base 2) 1001. . . 0000, 0001, 0010, 0011, 0100, 0101 0110 0111 1000 q decimal: 0, 1, 2, 3, . . . 2 n-1 [In this case, n=4] q Of course it gets more complicated: numbers are finite (overflow) fractions and real numbers --- (Introduce Floating Point) negative numbers q So, how do we, e. g. , represent negative numbers? That is, which bit patterns will represent which numbers?

Numbers 23 q 22 21 20 E. g. , 1 1 0 02 = 8 + 4 + 0 = 12 base ten

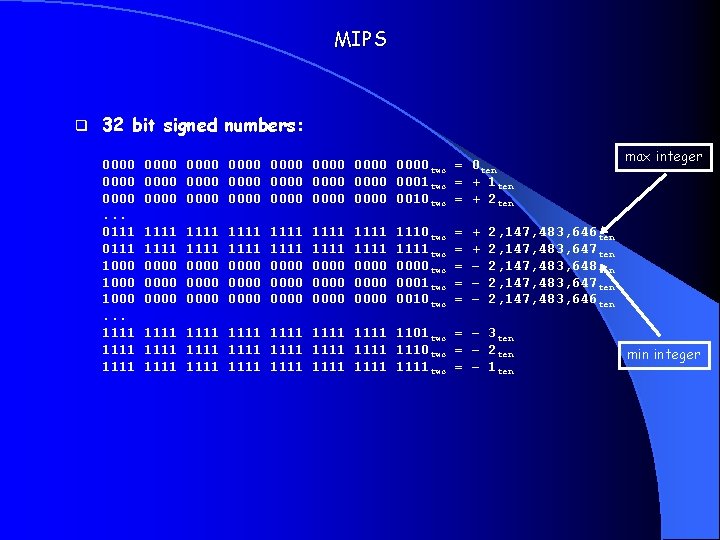
MIPS q 32 bit signed numbers: 0000. . . 0111 1000. . . 1111 0000 0000 two = 0 ten 0000 0000 0001 two = + 1 ten 0000 0000 0010 two = + 2 ten 1111 1111 0000 0000 0000 1111 0000 0000 1110 two 1111 two 0000 two 0001 two 0010 two = = = + + – – – max integer 2, 147, 483, 646 ten 2, 147, 483, 647 ten 2, 147, 483, 648 ten 2, 147, 483, 647 ten 2, 147, 483, 646 ten 1111 1111 1101 two = – 3 ten 1111 1111 1110 two = – 2 ten 1111 1111 two = – 1 ten min integer

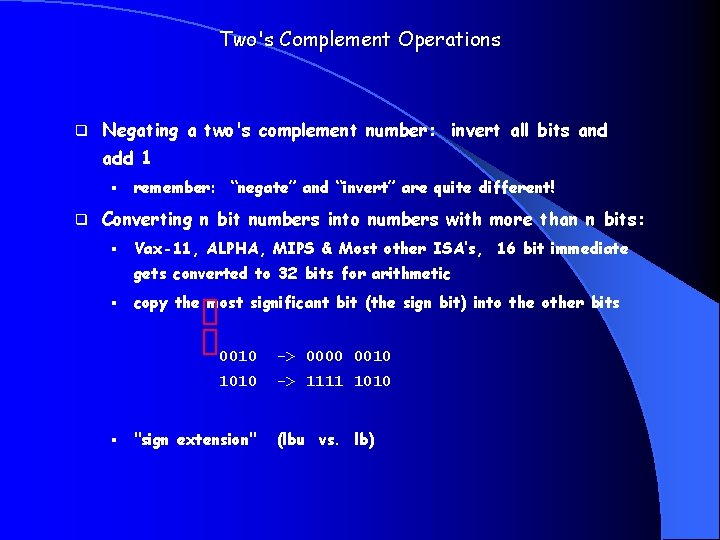
Two's Complement Operations q Negating a two's complement number: invert all bits and add 1 § q remember: “negate” and “invert” are quite different! Converting n bit numbers into numbers with more than n bits: § Vax-11, ALPHA, MIPS & Most other ISA’s, 16 bit immediate gets converted to 32 bits for arithmetic § § copy the most significant bit (the sign bit) into the other bits 0010 -> 0000 0010 1010 -> 1111 1010 "sign extension" (lbu vs. lb)

Addition & Subtraction q Just like in grade school (carry/borrow 1 s) 0111 0110 + 0110 - 0101 q Two's complement operations easy § q subtraction using addition of negative numbers 0111 + 1010 Overflow (result too large for finite computer word): § Two Positive #’s Result in negative e. g. , adding two n-bit numbers does not yield an n-bit number 0111 + 0001 note that overflow term is somewhat misleading, 1000 it does not mean a carry “overflowed”

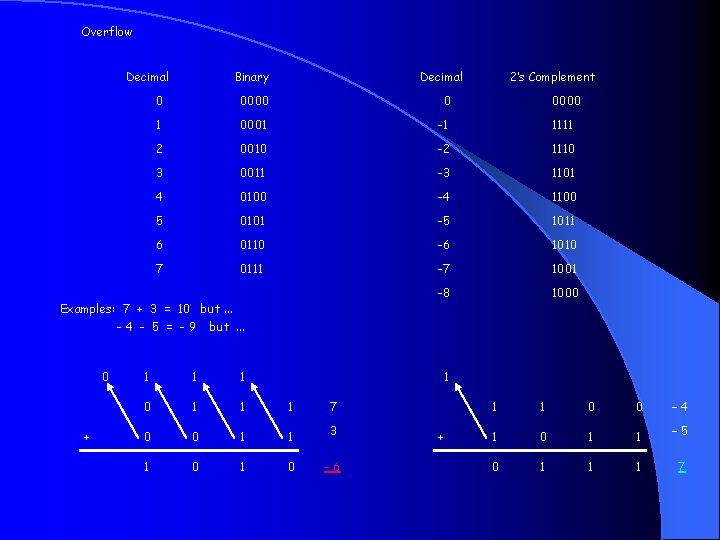
Overflow Decimal Binary Decimal 0 0000 0 1 0001 -1 1111 2 0010 -2 1110 3 0011 -3 1101 4 0100 -4 1100 5 0101 -5 1011 6 0110 -6 1010 7 0111 -7 1001 -8 1000 Examples: 7 + 3 = 10 but. . . - 4 - 5 = - 9 but. . . 0 + 2’s Complement 1 1 1 0 1 1 1 7 0 0 1 1 3 1 0 – 6 0000 1 + 1 1 0 0 – 4 1 0 1 1 – 5 0 1 1 1 7

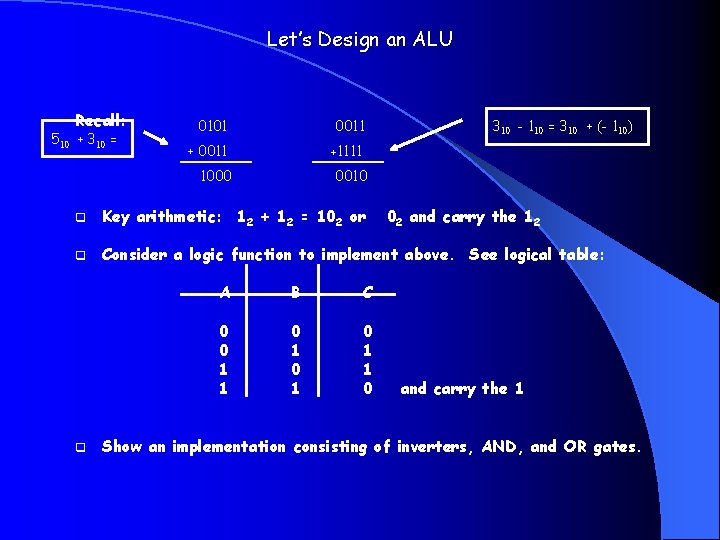
Let’s Design an ALU Recall: 510 + 310 = 0101 0011 +1111 1000 310 - 110 = 310 + (- 110) 0010 q Key arithmetic: 12 + 12 = 102 or q Consider a logic function to implement above. See logical table: q A B C 0 0 1 1 0 1 0 1 1 0 02 and carry the 1 Show an implementation consisting of inverters, AND, and OR gates.

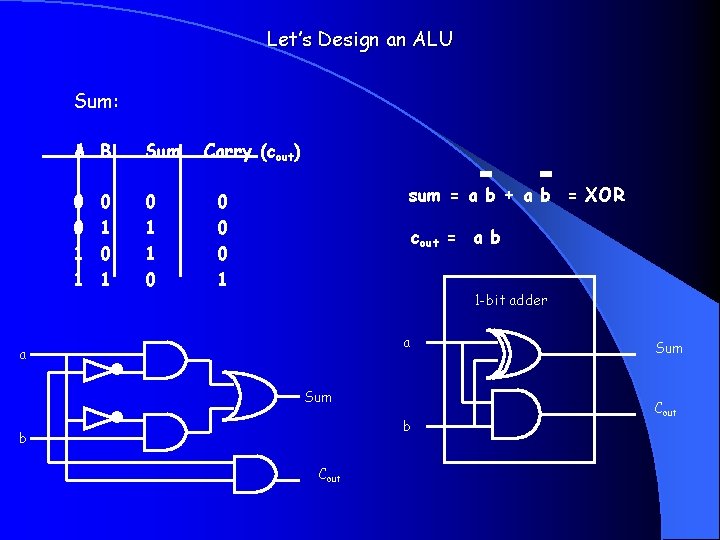
Let’s Design an ALU Sum: A B Sum 0 0 1 1 0 0 1 Carry (cout) sum = a b + a b = XOR 0 0 0 1 cout = a b 1 -bit adder a a Sum b b Cout Sum Cout

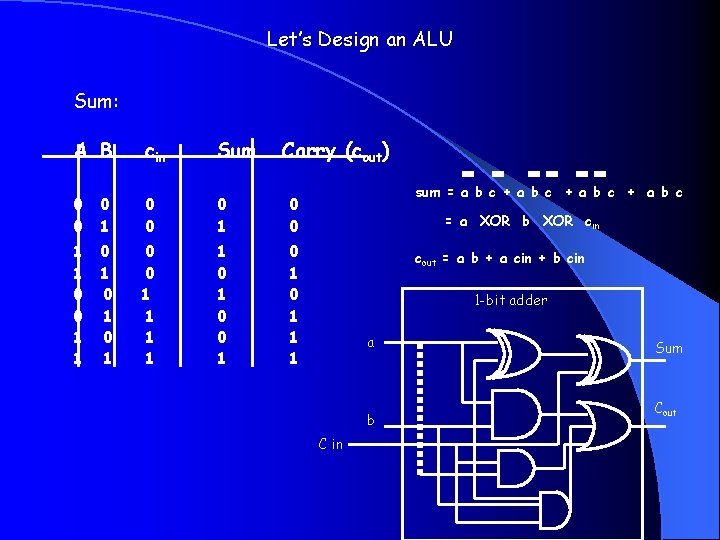
Let’s Design an ALU Sum: A B cin Sum Carry (cout) 0 0 0 1 1 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 sum = a b c + a b c = a XOR b XOR cin cout = a b + a cin + b cin 1 -bit adder a b C in Sum Cout

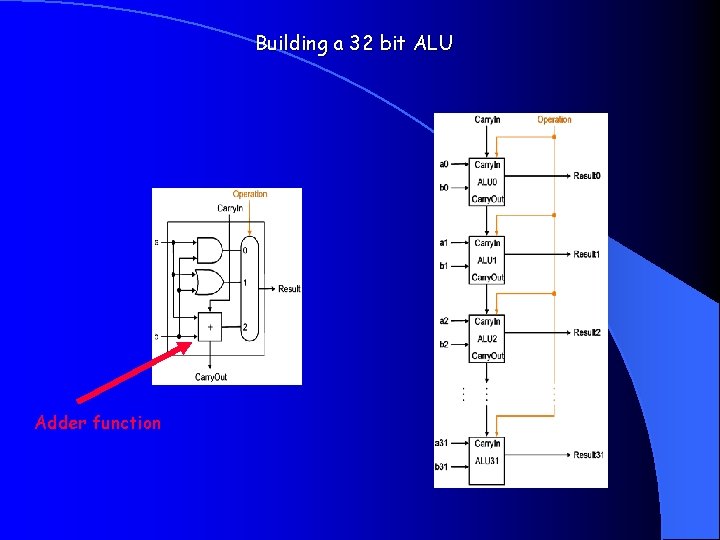
Building a 32 bit ALU Adder function

Assembly Language From C code /* File is junk. c */ int main(int argc, char **argv) { int x; x = 3 + 2; return (0); } ------------------> gcc -s junk. c

Intel Windows. Assembly Language output. file "junk. c" gcc 2_compiled. : ___gnu_compiled_c: . text. align 2. globl _main: pushl %ebp movl %esp, %ebp subl $4, %esp call ___main movl $5, -4(%ebp) xorl %eax, %eax jmp L 1. align 2, 0 x 90 L 1: leave ret <-- compiler smart enough to create a constant

Intel Windows Assembly Language output. file "junk. c" gcc 2_compiled. : ___gnu_compiled_c: . text. align 2. globl _main: pushl %ebp movl %esp, %ebp subl $4, %esp call ___main movl $5, -4(%ebp) xorl %eax, %eax jmp L 1. align 2, 0 x 90 L 1: leave ret <-- compiler smart enough to create a constant

Intel Linux Assembly Language output. file "junk. c". text. globl main. type main, @function main: pushl %ebp movl %esp, %ebp subl $8, %esp andl $-16, %esp movl $0, %eax subl %eax, %esp movl $5, -4(%ebp) movl $0, %eax leave ret. Lfe 1: . size main, . Lfe 1 -main. ident "GCC: (GNU) 3. 2. 2 20030222 (Red Hat Linux 3. 2. 2 -5)"

Sun Assembly Language output main . PROC. CALLINFO FRAME=128, CALLS, SAVE_RP, SAVE_SP, ENTRY_GR=3. ENTRY stw %r 2, -20(%r 30) copy %r 3, %r 1 copy %r 30, %r 3 stwm %r 1, 128(%r 30) stw %r 26, -36(%r 3) stw %r 25, -40(%r 3). CALL bl __main, %r 2 nop ldi 5, %r 19 stw %r 19, 8(%r 3) ldi 0, %r 28 ldw -20(%r 3), %r 2 ldo 64(%r 3), %r 30 ldwm -64(%r 30), %r 3 bv, n %r 0(%r 2). EXIT. PROCEND

Different Systems / Different architectures All architectures implement data types, and instructions. How they implement them is up to the designers of the underlying hardware (and also the operating system). Data types from one system may be implemented far differently from another system, even though symbolically they are the same. This is why Windows programs are often shipped as binary files ready to run (same Intel architecture) but Unix programs must fist be compiled on each machine (different architectures – Sun, Intel, HP, IBM…).

Different Systems / Different Architectures Distributed systems that interoperate between machines by shipping data and code to different processors must take into account the differences in Architectures. The process of translating bit representations from one system to another (as well as some intermediate state) is called marshalling and unmarshalling. With multicomputer Distributed Systems we often think of marshalling data from the source system into a serial form for network transmission, and then unmarshalling it from the network into the destination format.

Virtual Memory -- ouch But wait – that’s not all! We forgot about memory addressing.

Real addresses – just temporary Note that in NONE of the assembly code is there any reference to the variable “x”. X is a symbolic name which is translated into the address of a piece of memory big enough to hold an integer. (4 bytes? 8 bytes? ) At run time the loader assigns a temporary location in memory which will hold the value of x. We then refer to x by the address of that piece of memory. But – If the operating system needs the memory it will write the whole (running) program out to disk for a short time, then load it back in again later, often at a different location.

Memory – it’s ephemeral! When studying Distributed Systems we must have an understanding of concepts such as: Architectures Context Switching – process control blocks Data formats Memory Addressing Dynamically linked data structures http: //condor. depaul. edu/~elliott/420/ppt/memory/MIPS-memory. pdf http: //condor. depaul. edu/~elliott/420/ppt/memory/Memory. Addressing. ppt

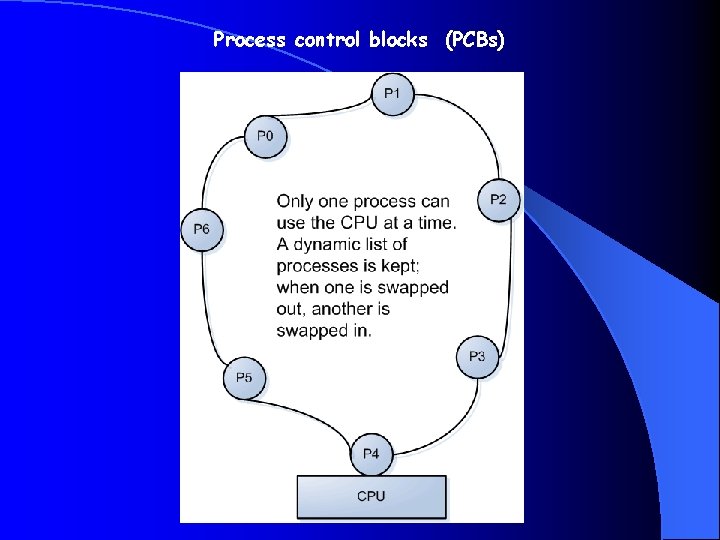
Process control blocks (PCBs)

Memory – only on loan when you need it When a process is swapped out it’s memory might be needed by other processes. When this happens, all of the real addresses become meaningless, and will have to be replaced by new addresses when the process is swapped back in. The operating system keeps symbol tables to know where the value of a program’s symbols (remember “x”? ) reside. When a process is restored to the CPU so that it can continue running, all of the values of its symbols (variables…) are retrieved from disk and placed back into new temporary memory locations. A new symbol table is created to bind the symbols to real memory locations.

The program counter A process is a program in execution. That is, the step -by-step execution of a set of instructions, in order. At any given moment, the process is executing one instruction. This instruction was loaded into the instruction register from a location in memory. That memory location is stored in the program counter, or “PC”. The program counter is incremented, and the instruction at the next memory location is loaded. When a process is swapped out, the PC is saved; when restarted the PC (updated to point to the new memory locations) tells us at which instruction to start.

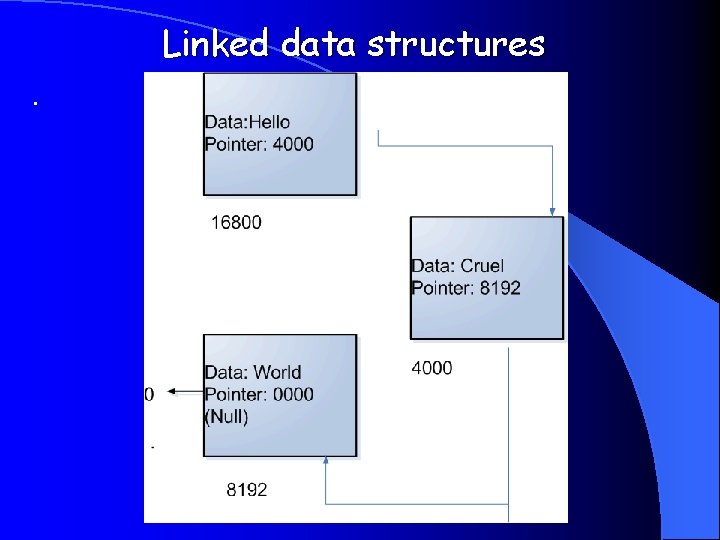
Linked data structures.

No symbol table on remote machine Generally speaking the symbol table that the operating system keeps for our local process allows us to relocate linked structures in memory after a context switch. However, a remote system has no symbol table for the local process. For this reason, marshalling can get very complex, if not impossible, for dynamically linked structures.

Summary -- bits Transistors put out 5 volts, or no volts. Combinations of transistors give us persistent memory. Symbolically, we see a memory location as a bit: either 1 or 0 Bit strings do not mean anything without an interpretation. Interpretations are arbitrary. System architects, who generally are interested in speed, and speed, tell us what the bit strings mean.

Summary –- bit strings Some bit strings are valid instructions, and get loaded into the instruction register. Logic gates, such as AND, OR, and NOT, are used to translate instruction bit strings into action. Other bit strings are data and are manipulated in CPU registers by the instructions. Different machines have different architectures – interpret the bit strings differently.

Summary -- memory Data and instructions are stored in memory. At link-time all symbolic addresses are translated into offsets from the beginning of the program. Symbolic values, such as variables, are translated into real addresses in memory at run time by adding offsets from the starting address of the program’s temporary memory location. Processes share the CPU. When a process is swapped out it may have to give up its memory.

Summary – symbol tables The operating system keeps a symbol table for each process, which binds symbolic values in a program to real memory locations. When a process is restored from disk, back into real memory, the symbol table is updated. The program counter is also restored –- but adjusted to the new location of the program in memory -- and execution continues where it left off.

Summary -- architectures Assembly language is generally translated line for line into bit strings. The same C program will produce very different assembly language for different machines because the underlying architecture (meaning of the bit strings) is very different.

Summary -- Marshalling is hard. Shipping programs, and data, from one machine to another in a distributed system means translating bit strings on one machine into some (usually serial) agreed -upon external format, and then translated again into (possibly very different) bit strings at the other end. Data formats, and instruction formats, may be different. Memory addresses are meaningless. Symbol tables do not exist on the remote system. In addition, it is possible that no general algorithm exists for marshalling dynamically linked data structures.