SE 301 Numerical Methods Topic 8 Ordinary Differential

SE 301: Numerical Methods Topic 8 Ordinary Differential Equations (ODEs) Lecture 28 -36 KFUPM Read 25. 1 -25. 4, 26 -2, 27 -1 CISE 301_Topic 8 L 4&5 KFUPM 1

Outline of Topic 8 Lesson 1: Introduction to ODEs p Lesson 2: Taylor series methods p Lesson 3: Midpoint and Heun’s method p Lessons 4 -5: Runge-Kutta methods p Lesson 6: Solving systems of ODEs p Lesson 7: Multiple step Methods p Lesson 8 -9: Boundary value Problems p CISE 301_Topic 8 L 4&5 KFUPM 2

Lecture 31 Lesson 4: Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM 3

Learning Objectives of Lesson 4 p p p To understand the motivation for using Runge Kutta method and the basic idea used in deriving them. To Familiarize with Taylor series for functions of two variables. Use Runge Kutta of order 2 to solve ODEs. CISE 301_Topic 8 L 4&5 KFUPM 4

Motivation p p We seek accurate methods to solve ODEs that do not require calculating high order derivatives. The approach is to use a formula involving unknown coefficients then determine these coefficients to match as many terms of the Taylor series expansion. CISE 301_Topic 8 L 4&5 KFUPM 5

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 6

Taylor Series in Two Variables The Taylor Series discussed in Chapter 4 is extended to the 2 -independent variable case. This is used to prove RK formula. CISE 301_Topic 8 L 4&5 KFUPM 7

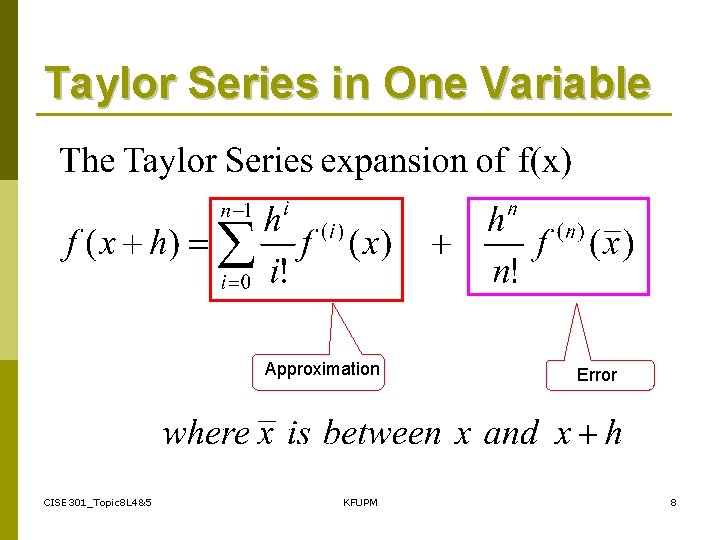
Taylor Series in One Variable Approximation CISE 301_Topic 8 L 4&5 KFUPM Error 8

Taylor Series in One Variable - Another Look - CISE 301_Topic 8 L 4&5 KFUPM 9

Definitions CISE 301_Topic 8 L 4&5 KFUPM 10

Taylor Series Expansion CISE 301_Topic 8 L 4&5 KFUPM 11

Taylor Series in Two Variables y+k y x CISE 301_Topic 8 L 4&5 x+h KFUPM 12

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 13

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 14

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 15

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 16

Runge-Kutta Method Alternative Formula CISE 301_Topic 8 L 4&5 KFUPM 17

Runge-Kutta Method Alternative Formula CISE 301_Topic 8 L 4&5 KFUPM 18

Runge-Kutta Method Alternative Formulas CISE 301_Topic 8 L 4&5 KFUPM 19

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 20

Second order Runge-Kutta Method Example CISE 301_Topic 8 L 4&5 KFUPM 21

Second order Runge-Kutta Method Example CISE 301_Topic 8 L 4&5 KFUPM 22

Second order Runge-Kutta Method Example CISE 301_Topic 8 L 4&5 KFUPM 23

CISE 301_Topic 8 L 4&5 KFUPM 24

Summary Runge Kutta methods generate an accurate solution without the need to calculate high order derivatives. p Second order RK have local truncation error of order O(h 3). p Fourth order RK have local truncation error of order O(h 5). p N function evaluations are needed in the Nth order RK method. p CISE 301_Topic 8 L 4&5 KFUPM 25

Lecture 32 Lesson 5: Applications of Runge-Kutta Methods to Solve First Order ODEs CISE 301_Topic 8 L 4&5 KFUPM 26

Learning Objectives of Lesson 5 p Use Runge-Kutta methods of different orders to solve first order ODEs. CISE 301_Topic 8 L 4&5 KFUPM 27

Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 28

Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM RK 2 29

Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM RK 3 30

Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM RK 4 31

Runge-Kutta Methods Higher order Runge-Kutta methods are available. Higher order methods are more accurate but require more calculations. Fourth order is a good choice. It offers good accuracy with a reasonable calculation effort. CISE 301_Topic 8 L 4&5 KFUPM 32

Fifth Order Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM 33

Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 34

Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 35

Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 36

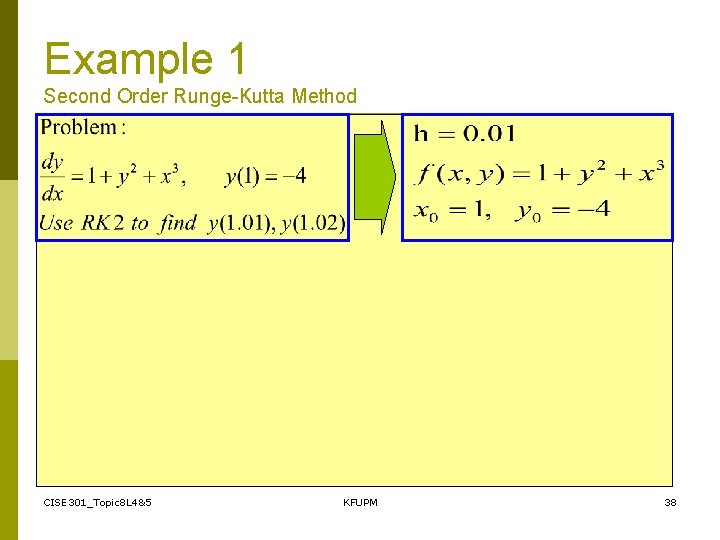
Example 1 Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 37

Example 1 Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 38

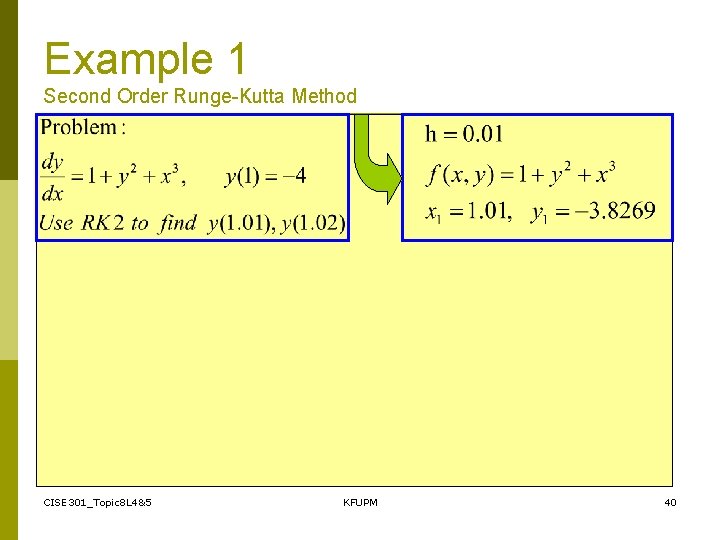
Example 1 Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 39

Example 1 Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 40

Example 1 Second Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 41

Example 1 Summary of the solution CISE 301_Topic 8 L 4&5 KFUPM 42

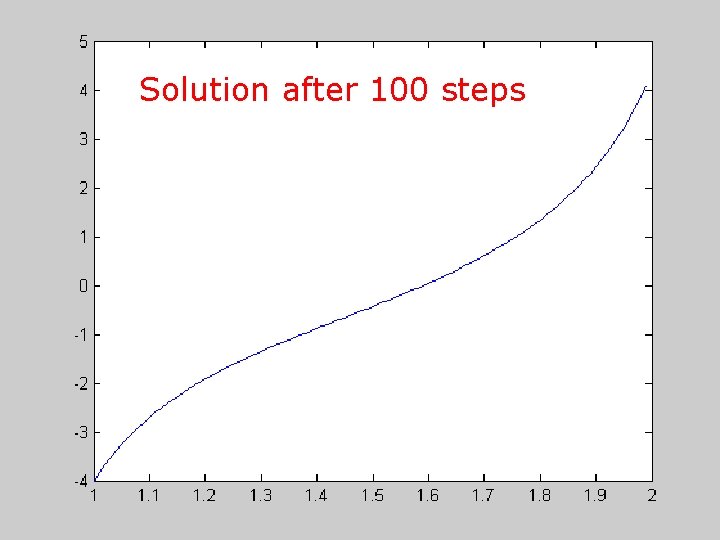
Solution after 100 steps CISE 301_Topic 8 L 4&5 KFUPM 43

Example 2 See RK 4 Formula 4 th-Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 44

Example 2 Fourth Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 45

Example 2 Fourth Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM See RK 4 Formula 46

Runge-Kutta Methods CISE 301_Topic 8 L 4&5 KFUPM RK 4 47

Example 2 Fourth Order Runge-Kutta Method CISE 301_Topic 8 L 4&5 KFUPM 48

Example 2 Summary of the solution CISE 301_Topic 8 L 4&5 KFUPM 49

Remaining Lessons in Topic 8 Lesson 6: Solving Systems of high order ODE Lesson 7: Multi-step methods Lessons 8 -9: Methods to solve Boundary Value Problems CISE 301_Topic 8 L 4&5 KFUPM 50