SE 301 Numerical Methods Topic 7 Numerical Integration

SE 301: Numerical Methods Topic 7 Numerical Integration Lecture 24 -27 KFUPM Read Chapter 21, Section 1 Read Chapter 22, Sections 2 -3 CISE 301_Topic 7 KFUPM 1

Lecture 24 Introduction to Numerical Integration p p p Definitions Upper and Lower Sums Trapezoid Method (Newton-Cotes Methods) Romberg Method Gauss Quadrature Examples CISE 301_Topic 7 KFUPM 2

Integration Indefinite Integrals Definite Integrals Indefinite Integrals of a function are functions that differ from each other by a constant. Definite Integrals are numbers. CISE 301_Topic 7 KFUPM 3

Fundamental Theorem of Calculus CISE 301_Topic 7 KFUPM 4

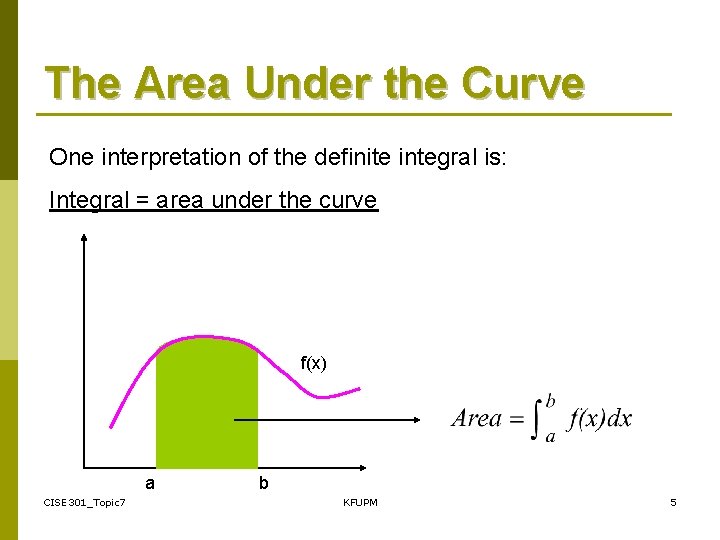
The Area Under the Curve One interpretation of the definite integral is: Integral = area under the curve f(x) a CISE 301_Topic 7 b KFUPM 5

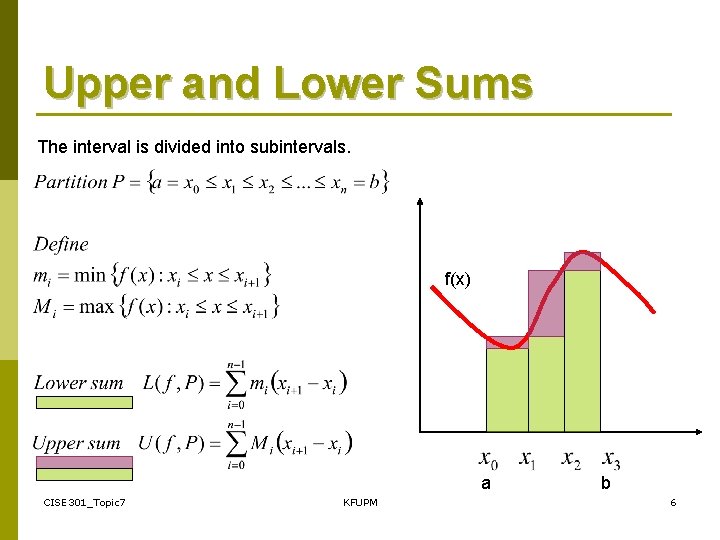
Upper and Lower Sums The interval is divided into subintervals. f(x) a CISE 301_Topic 7 KFUPM b 6

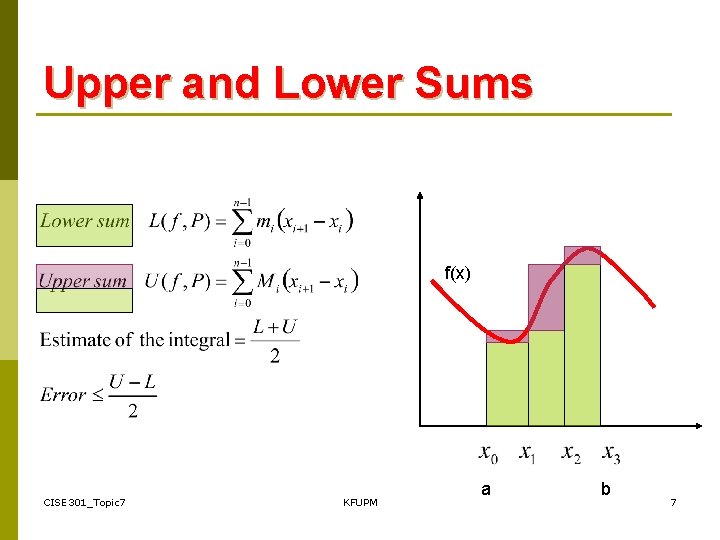
Upper and Lower Sums f(x) CISE 301_Topic 7 KFUPM a b 7

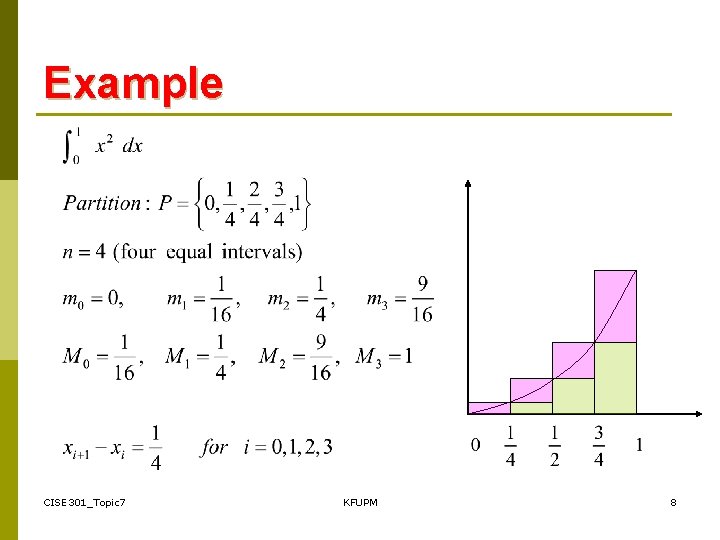
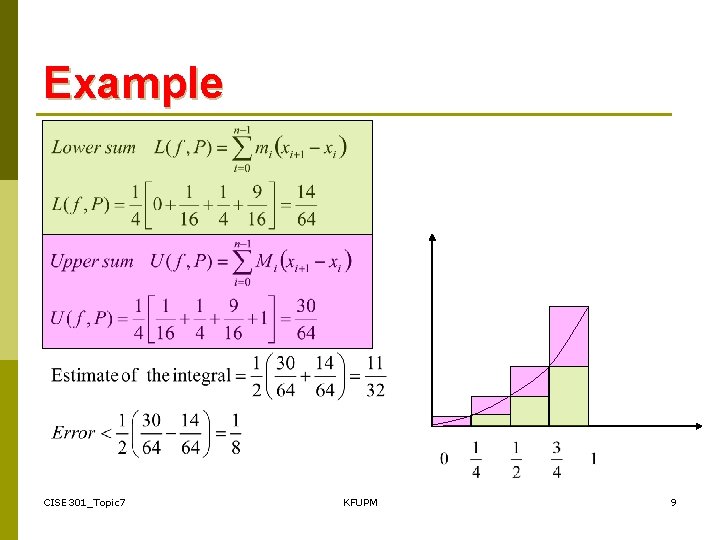
Example CISE 301_Topic 7 KFUPM 8

Example CISE 301_Topic 7 KFUPM 9

Upper and Lower Sums • Estimates based on Upper and Lower Sums are easy to obtain for monotonic functions (always increasing or always decreasing). • For non-monotonic functions, finding maximum and minimum of the function can be difficult and other methods can be more attractive. CISE 301_Topic 7 KFUPM 10

Newton-Cotes Methods In Newton-Cote Methods, the function is approximated by a polynomial of order n. p Computing the integral of a polynomial is easy. p CISE 301_Topic 7 KFUPM 11

Newton-Cotes Methods n Trapezoid Method (First Order Polynomials are used) n Simpson 1/3 Rule (Second Order Polynomials are used) CISE 301_Topic 7 KFUPM 12

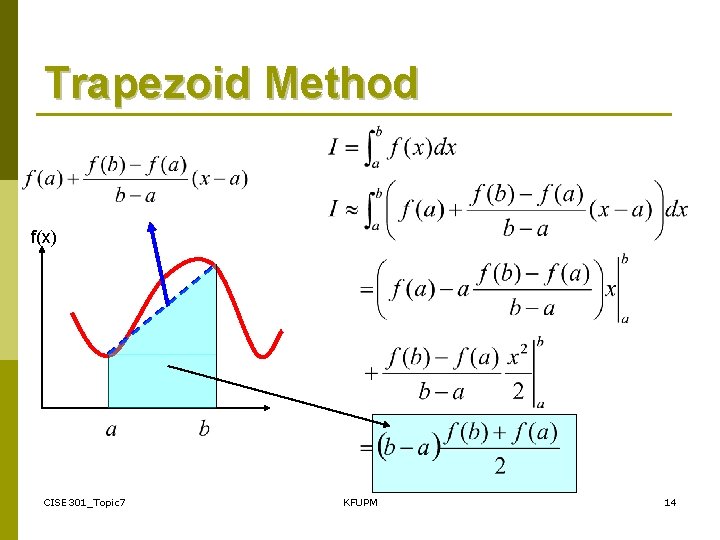
Lecture 25 Trapezoid Method p p Derivation-One Interval Multiple Application Rule Estimating the Error Recursive Trapezoid Method Read 21. 1 CISE 301_Topic 7 KFUPM 13

Trapezoid Method f(x) CISE 301_Topic 7 KFUPM 14

Trapezoid Method Derivation-One Interval CISE 301_Topic 7 KFUPM 15

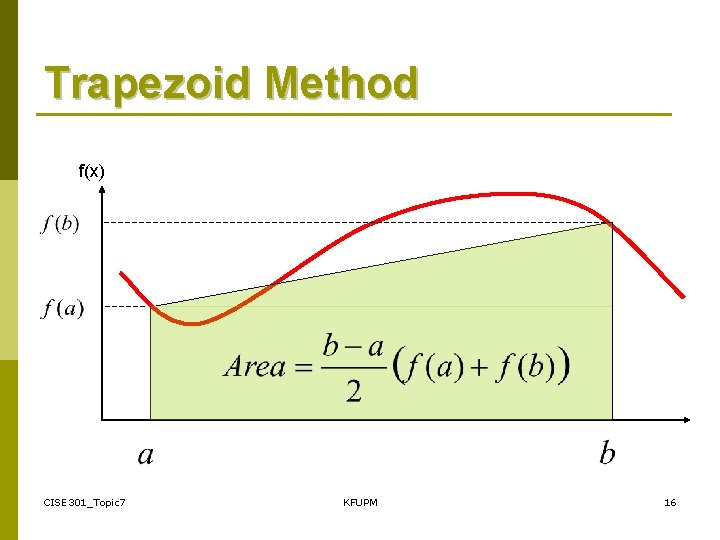
Trapezoid Method f(x) CISE 301_Topic 7 KFUPM 16

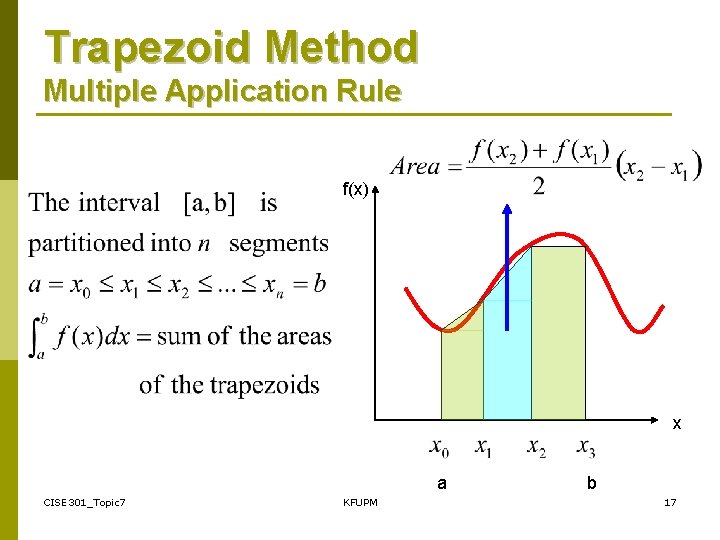
Trapezoid Method Multiple Application Rule f(x) x a CISE 301_Topic 7 KFUPM b 17

Trapezoid Method General Formula and Special Case CISE 301_Topic 7 KFUPM 18

Example Given a tabulated values of the velocity of an object. Time (s) 0. 0 1. 0 2. 0 3. 0 Velocity (m/s) 0. 0 10 12 14 Obtain an estimate of the distance traveled in the interval [0, 3]. Distance = integral of the velocity CISE 301_Topic 7 KFUPM 19

Example 1 CISE 301_Topic 7 Time (s) 0. 0 1. 0 2. 0 3. 0 Velocity (m/s) 0. 0 10 12 14 KFUPM 20

Estimating the Error For Trapezoid Method CISE 301_Topic 7 KFUPM 21

Error in estimating the integral Theorem CISE 301_Topic 7 KFUPM 22

Example CISE 301_Topic 7 KFUPM 23

Example x 1. 0 1. 5 2. 0 2. 5 3. 0 f(x) 2. 1 3. 2 3. 4 2. 8 2. 7 CISE 301_Topic 7 KFUPM 24

Example x 1. 0 1. 5 2. 0 2. 5 3. 0 f(x) 2. 1 3. 2 3. 4 2. 8 2. 7 CISE 301_Topic 7 KFUPM 25

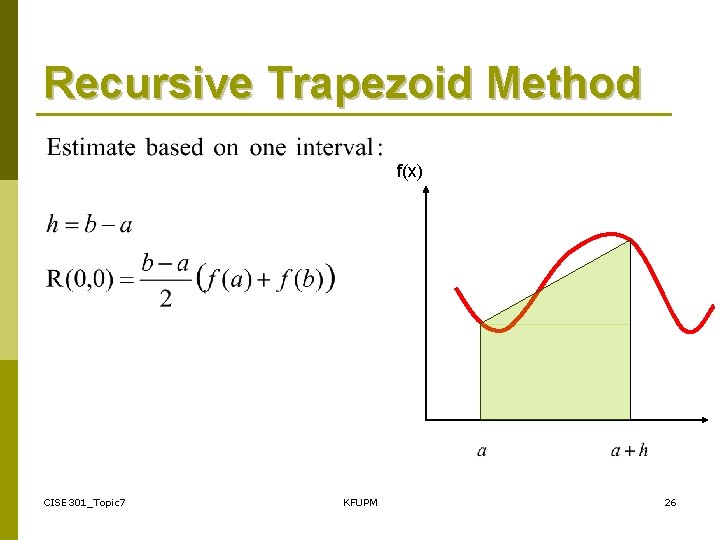
Recursive Trapezoid Method f(x) CISE 301_Topic 7 KFUPM 26

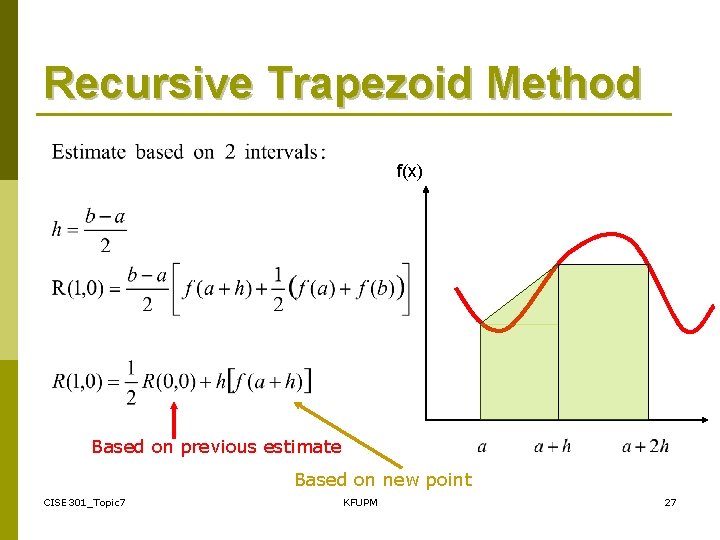
Recursive Trapezoid Method f(x) Based on previous estimate Based on new point CISE 301_Topic 7 KFUPM 27

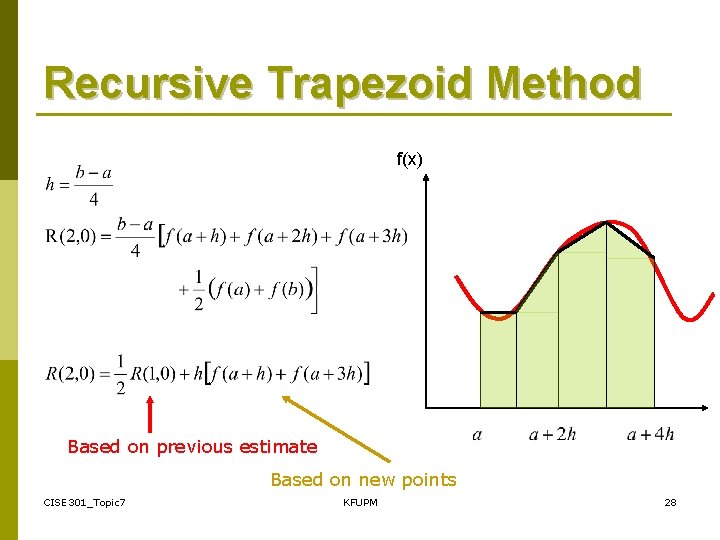
Recursive Trapezoid Method f(x) Based on previous estimate Based on new points CISE 301_Topic 7 KFUPM 28

Recursive Trapezoid Method Formulas CISE 301_Topic 7 KFUPM 29

Recursive Trapezoid Method CISE 301_Topic 7 KFUPM 30

Advantages of Recursive Trapezoid: p Gives the same answer as the standard Trapezoid method. p Makes use of the available information to reduce the computation time. p Useful if the number of iterations is not known in advance. CISE 301_Topic 7 KFUPM 31

Lecture 26 Romberg Method p p p Motivation Derivation of Romberg Method Example When to stop? Read 22. 2 CISE 301_Topic 7 KFUPM 32

Motivation for Romberg Method p Trapezoid formula with an interval h gives an error of the order O(h 2). p We can combine two Trapezoid estimates with intervals 2 h and h to get a better estimate. CISE 301_Topic 7 KFUPM 33

Romberg Method First column is obtained using Trapezoid Method R(0, 0) R(1, 1) R(2, 0) R(2, 1) R(2, 2) R(3, 0) R(3, 1) R(3, 2) R(3, 3) The other elements are obtained using the Romberg Method CISE 301_Topic 7 KFUPM 34

First Column Recursive Trapezoid Method CISE 301_Topic 7 KFUPM 35

Derivation of Romberg Method CISE 301_Topic 7 KFUPM 36

Romberg Method R(0, 0) R(1, 1) R(2, 0) R(2, 1) R(2, 2) R(3, 0) R(3, 1) R(3, 2) CISE 301_Topic 7 KFUPM R(3, 3) 37

Property of Romberg Method R(0, 0) R(1, 1) R(2, 0) R(2, 1) R(2, 2) R(3, 0) R(3, 1) R(3, 2) R(3, 3) Error Level CISE 301_Topic 7 KFUPM 38

Example 1 0. 5 3/8 1/3 CISE 301_Topic 7 KFUPM 39

Example 1 (cont. ) CISE 301_Topic 7 KFUPM 0. 5 3/8 1/3 11/32 1/3 40

When do we stop? CISE 301_Topic 7 KFUPM 41

Lecture 27 Gauss Quadrature p p Motivation General integration formula Read 22. 3 CISE 301_Topic 7 KFUPM 42

Motivation CISE 301_Topic 7 KFUPM 43

General Integration Formula CISE 301_Topic 7 KFUPM 44

Lagrange Interpolation CISE 301_Topic 7 KFUPM 45

Question What is the best way to choose the nodes and the weights? CISE 301_Topic 7 KFUPM 46

Theorem CISE 301_Topic 7 KFUPM 47

Weighted Gaussian Quadrature Theorem CISE 301_Topic 7 KFUPM 48

Determining The Weights and Nodes CISE 301_Topic 7 KFUPM 49

Determining The Weights and Nodes Solution CISE 301_Topic 7 KFUPM 50

Determining The Weights and Nodes Solution CISE 301_Topic 7 KFUPM 51

Determining The Weights and Nodes Solution CISE 301_Topic 7 KFUPM 52

Gaussian Quadrature See more in Table 22. 1 (page 626) CISE 301_Topic 7 KFUPM 53

Error Analysis for Gauss Quadrature CISE 301_Topic 7 KFUPM 54

Example CISE 301_Topic 7 KFUPM 55

Example CISE 301_Topic 7 KFUPM 56

Improper Integrals CISE 301_Topic 7 KFUPM 57