Scientific Visualization Data Modelling for Scientific Visualization CS

Scientific Visualization Data Modelling for Scientific Visualization CS 5630 / 6630 August 28, 2007

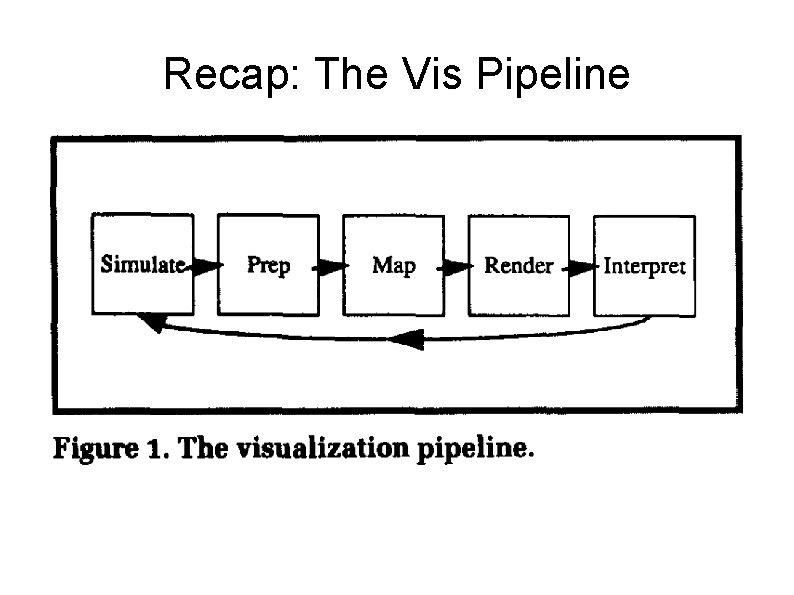
Recap: The Vis Pipeline

Recap: The Vis Pipeline

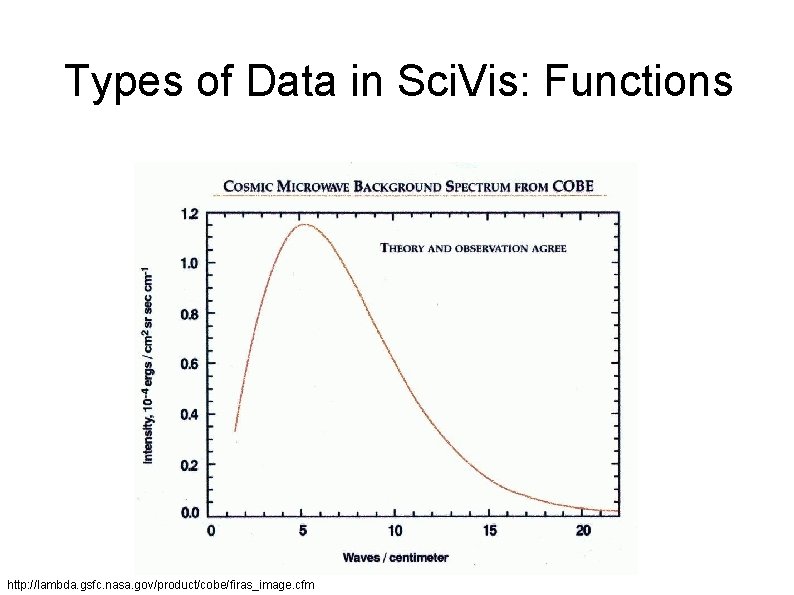
Types of Data in Sci. Vis: Functions http: //lambda. gsfc. nasa. gov/product/cobe/firas_image. cfm

Types of Data in Sci. Vis: Functions on Circles E. Anderson et al. : Towards Development of a Circuit Based Treatment for Impaired Memory

Types of Data in Sci. Vis: 2 D Scalar Fields

Types of Data in Sci. Vis: Scalar Fields on Spheres http: //lambda. gsfc. nasa. gov/product/cobe/firas_image. cfm

Types of Data in Sci. Vis: 3 D, time-varying Scalar Fields http: //background. uchicago. edu/~whu/beginners/introduction. html

Types of Data in Sci. Vis: 2 D Vector Fields

Types of Data in Sci. Vis: 3 D Vector Fields

Tensors are “multilinear functions” rank 0 tensors are scalars rank 1 tensors are vectors rank 2 tensors are matrices, which transform vectors rank 3. . n tensors have no nice name, but they transform matrices, rank-3 tensors, etc. We are not going to see these

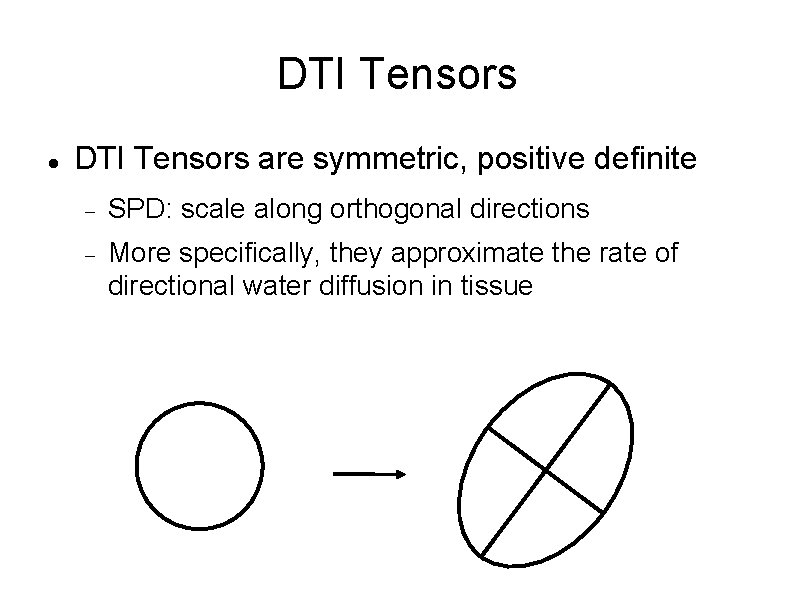
DTI Tensors are symmetric, positive definite SPD: scale along orthogonal directions More specifically, they approximate the rate of directional water diffusion in tissue

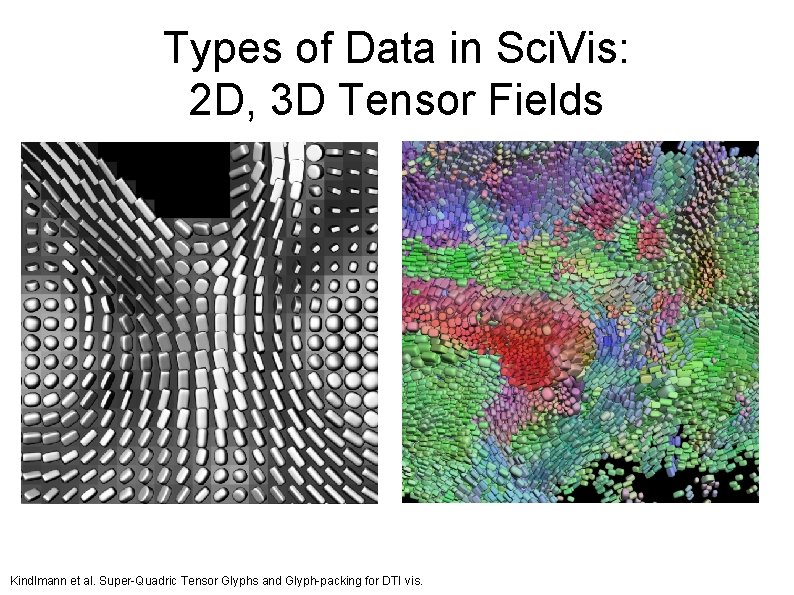
Types of Data in Sci. Vis: 2 D, 3 D Tensor Fields Kindlmann et al. Super-Quadric Tensor Glyphs and Glyph-packing for DTI vis.

Computers like discrete data, but world is continuous

Sampling Continuous to discrete Store properties at a finite set of points

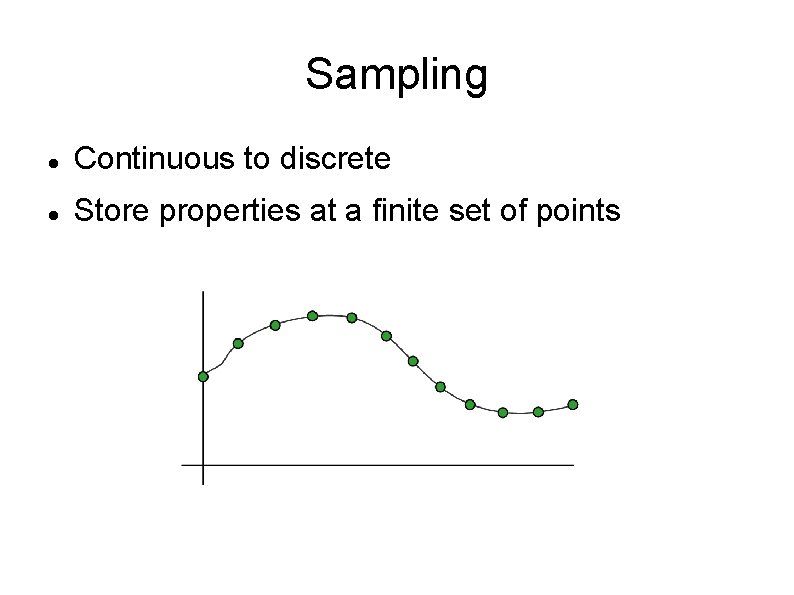
Sampling Continuous to discrete Store properties at a finite set of points

Sampling Continuous to discrete Store properties at a finite set of points

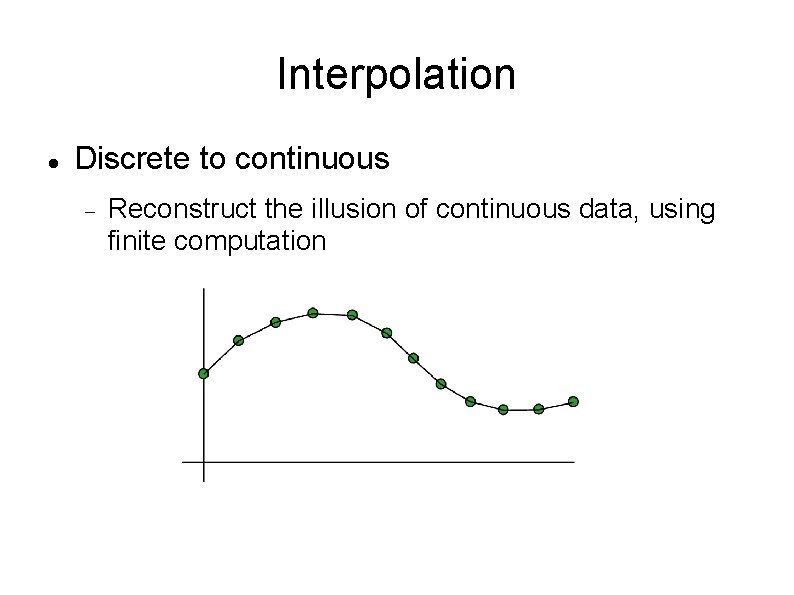
Interpolation Discrete to continuous Reconstruct the illusion of continuous data, using finite computation

Nearest Neighbor Interpolation Pick the closest value to you

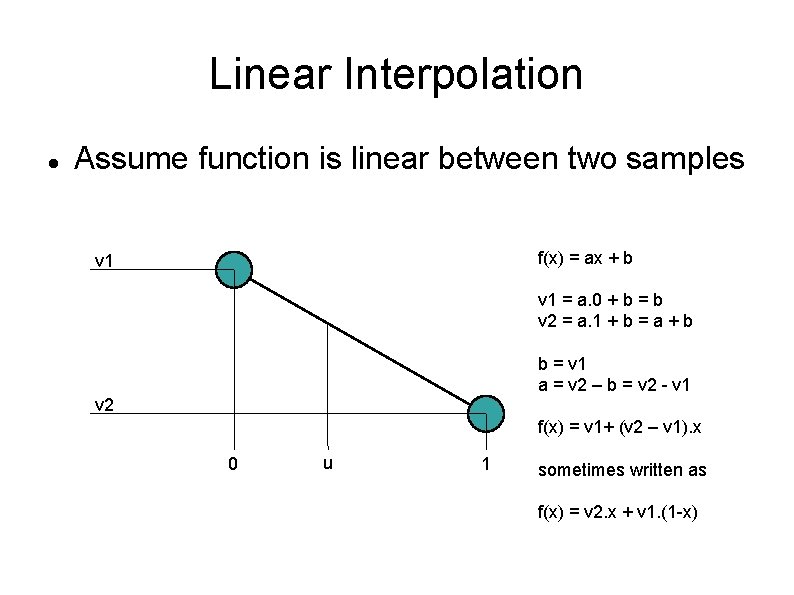
Linear Interpolation Assume function is linear between two samples

Linear Interpolation Assume function is linear between two samples f(x) = ax + b v 1 = a. 0 + b = b v 2 = a. 1 + b = a + b b = v 1 a = v 2 – b = v 2 - v 1 v 2 f(x) = v 1+ (v 2 – v 1). x 0 u 1 sometimes written as f(x) = v 2. x + v 1. (1 -x)

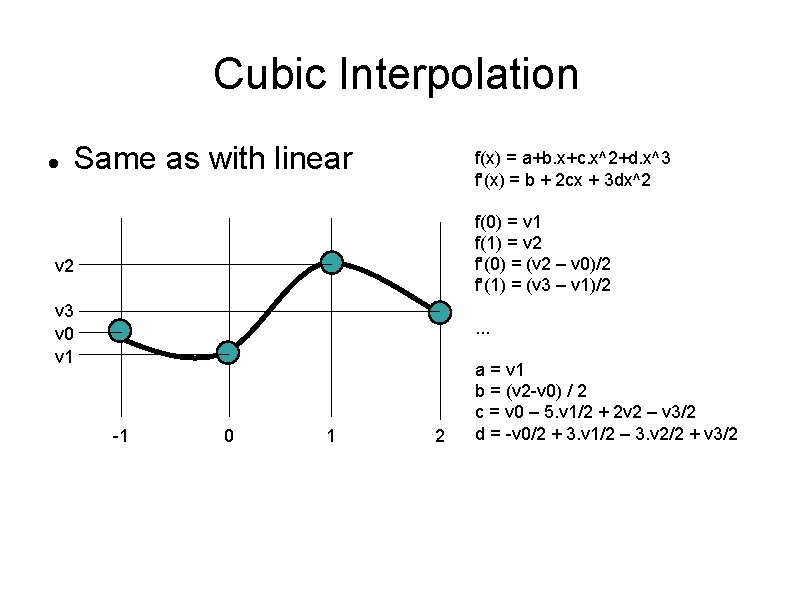
Cubic Interpolation Linear reconstruction is better than NN, but it is not smooth across sample points Let's use a cubic Two more parameters: we need constraints Constrain derivatives

Cubic Interpolation Same as with linear f(x) = a+b. x+c. x^2+d. x^3 f'(x) = b + 2 cx + 3 dx^2 f(0) = v 1 f(1) = v 2 f'(0) = (v 2 – v 0)/2 f'(1) = (v 3 – v 1)/2 v 3 v 0 v 1 . . . -1 0 1 2 a = v 1 b = (v 2 -v 0) / 2 c = v 0 – 5. v 1/2 + 2 v 2 – v 3/2 d = -v 0/2 + 3. v 1/2 – 3. v 2/2 + v 3/2

(Vis. Trails Demo) Linear vs Higher-order interpolation in plotting

Might make a big difference! Kindlmann et al. Geodesic-loxodromes. . . MICCAI 2007

1 D vs n-D Most common technique: separability Interpolate dimensions one at a time

(Vis. Trails Demo) 2 D Interpolation in VTK images

Implicit vs Explicit Representations Explicit is parametric Domain and range are “explicit” Implicit stores domain. . . implicitly Zero set of a explicit domain Pro: it's easy to change topology of domain: just change the function Con: it's harder to analyze and compute with

Implicit vs. explicit representations Explicit: y(t) = sin(t) x(t) = cos(t) Implicit: f(x, y) = x^2 + y^2 - 1 s = (x(t), y(t)), 0 < t <= 2 s = (x, y): f(x, y) = 0

Regular vs Irregular Data Regular data: sampling on every point of an integer lattice Irregular data: more general sampling

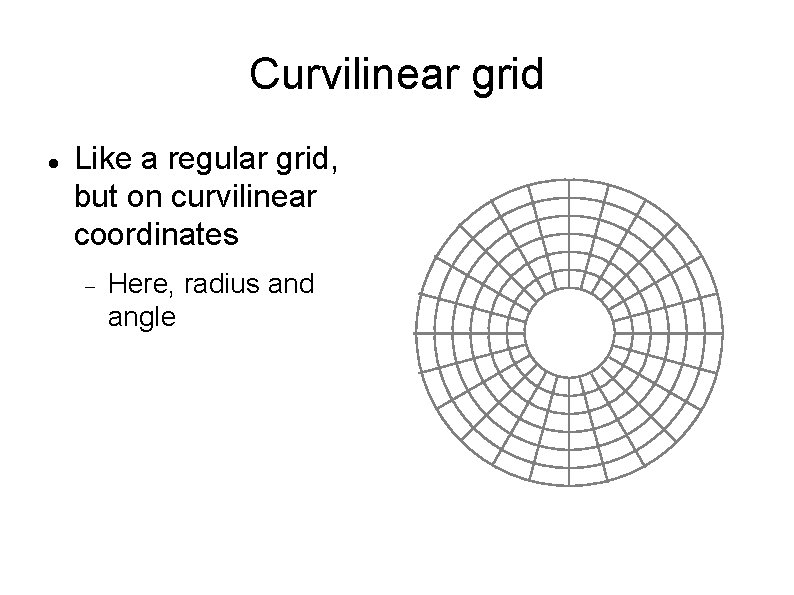
Curvilinear grid Like a regular grid, but on curvilinear coordinates Here, radius and angle

Triangular and Tetrahedral Meshes Completely arbitrary samples Need to store topology: How do samples connect with one another?

Quadrilateral and Hexahedral Meshes Basic element is a quad or a hex Element shape is better for computation Much, much harder to generate

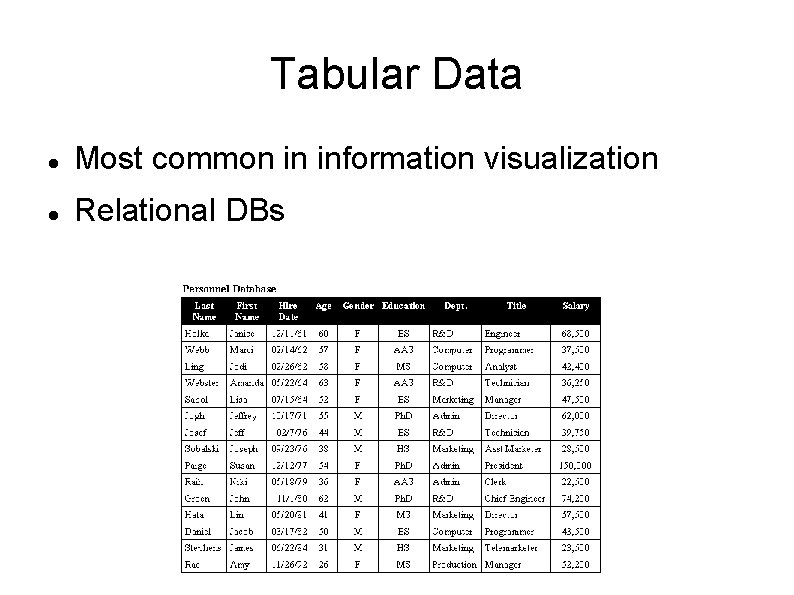
Tabular Data Most common in information visualization Relational DBs

. . . etc. Node vs cell data: do we store values on nodes (vertices) or on cells (tets and tris)? Pure-quad vs quad-dominant: mixing types of elements Linear vs high-order: different interpolation modes on elements