Scientific Notation What is scientific Notation na way




















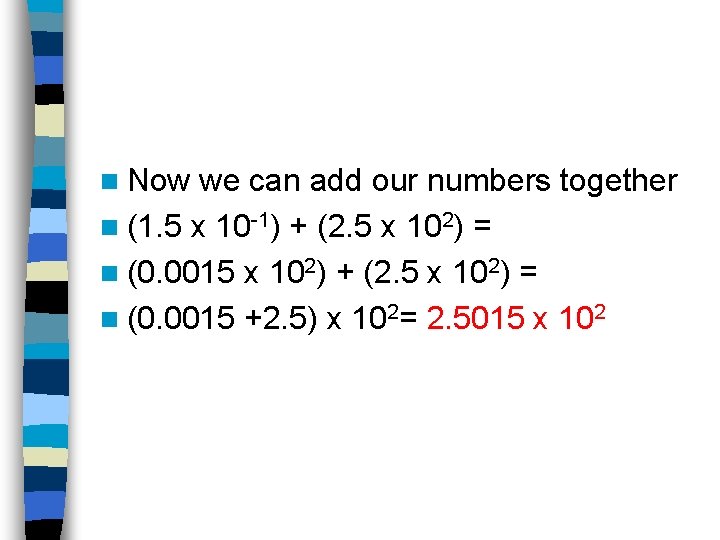







- Slides: 30

Scientific Notation

What is scientific Notation? na way of expressing really big numbers or really small numbers in a more concise form.

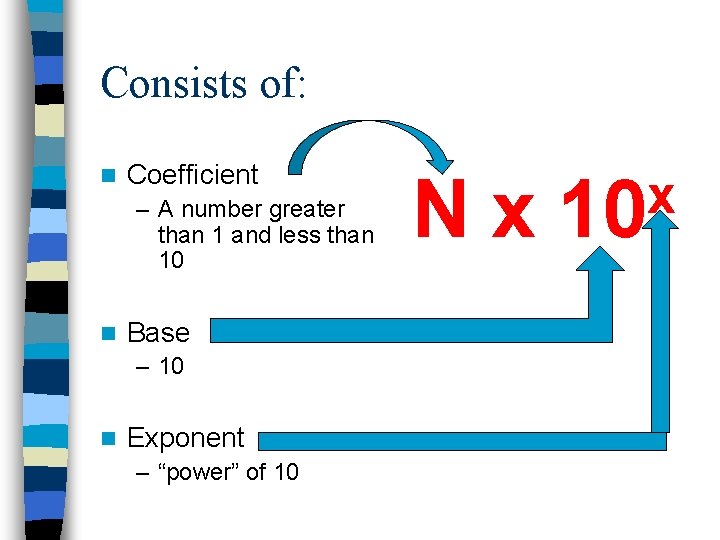
Consists of: n Coefficient – A number greater than 1 and less than 10 n Base – 10 n Exponent – “power” of 10 Nx x 10

n Scientific Notation 6. 02 x 106 m n Standard form 6, 020, 000 m

To change standard form to scientific notation… n Place the decimal point so that there is one non-zero digit to the left of the decimal point. n Count the number of decimal places the decimal point has “moved” from the original number. This will be the exponent on the 10.

Continued… n If the original number in standard form was less than 1, then the exponent is negative. n If the original number in standard form was greater than 1, then the exponent is positive.

Example 1 Convert 289, 800, 000 to scientific notation n Place the decimal so there is one non-zero digit to its left : – 289, 800, 000 2. 898 Count the number of places the decimal was moved to determine exponent – moved 8 places, so exponent is 8 n Determine if exponent is + or – based on value of number in standard form n – Original number in standard form is greater than one, so exponent is + n Final Answer: 2. 898 x 108

Example 2 Convert 0. 000567 to scientific notation n Place the decimal so there is one non-zero digit to its left : – 0. 000567 5. 67 Count the number of places the decimal was moved to determine exponent – moved 4 places, so exponent is 4 n Determine if exponent is + or – based on value of number in standard form n – Original number in standard form is less than one, so exponent is n Final Answer: 5. 67 x 10 -4

Practice n Use the link below to practice converting standard form to scientific notation. – Converting to Scientific Notation

To change scientific notation to standard form… Just move the decimal the number of places given by the exponent n Positive exponents will result in numbers greater than one when in standard form – So just think “which way do I move the decimal to make the resulting number greater than one? ” – To the right! n Negative exponents will result in numbers less than one when in standard form – So just think “which way do I move the decimal to make the resulting number less than one? ” – To the left! (Use zeros as placeholders!) n

Example 3 n n n Convert 5. 093 x 106 to standard form. The exponent is 6, so move the decimal 6 places. The exponent is positive, meaning the result in standard form is greater than one. – Decimal must be moved to the right to get a result greater than one. 5. 093 000 (note that three 0’s needed to hold places) Answer: 5, 093, 000 (moved 6 places to the right)

Example 4 n n n Convert 1. 976 x 10 -4 to standard form. The exponent is 4, so move the decimal 4 places. The exponent is negative, meaning the result in standard form is less than one. – Decimal must be moved to the left to get a result less than one. 00001. 976 (note the 0’s added as placeholders) Answer: 0. 0001976 (moved 4 places to the left)

Practice n Use the link below to practice converting scientific notation to standard form – Converting to Standard Form

Even More Practice n Below is a list of links to games and activities all having to do with scientific notation. – http: //www. aaamath. com/dec 71 idec 2 sci. html – http: //janus. astro. umd. edu/cgibin/astro/scinote. pl – http: //www. sciencejoywagon. com/physicsz one/lesson/00 genral/dectosci. htm

Now take the quiz to test your scientific notation skills! n Click on the link below to take the quiz and then use the answer key for the correct answers. – Quiz – Answers

Using scientific notation in calculations: multiplication and division n When multiplying numbers in scientific notation, multiply the coefficients and add the exponents. n When dividing numbers in scientific notation, divide the coefficients and subtract the exponents.

Example 5 n (2. 0 x 105) x (1. 5 x 10 -2)= ? n Multiply the coefficients 2. 0 x 1. 5=3. 0 n Add the exponents 5 + (-2) = 3 (new exponent) n Answer: 3. 0 x 103

Example 6 n (6. 0 x 105) / (1. 5 x 10 -2)= ? n Divide the coefficients 6. 0 / 1. 5= 4. 0 n Subtract the exponents 5 - (-2) = 7 (new exponent) n Answer: 4. 0 x 107

Using scientific notation in calculations: addition and subtraction n When adding or subtracting numbers in scientific notation, the exponents MUST MATCH (unless you punch it into a calculator!) n The exponent on the final answer is the same as the exponent on the terms in the problem.

Changing the exponent n (1. 5 x 10 -1) + (2. 5 x 102) = ? ? n The first thing we have to do is make our exponents match- they both either need to be -1 or 2, it doesn’t matter which, as long as they match, without changing the magnitude (value) of the quantity represented.

n 1. 5 x 10 -1 = _____x 102 – We are moving three powers of 10 to get from -1 to 2 (10 -1 100 101 102) – Think : 2 – (-1)= 3 – So we need to move our decimal 3 places – Now which direction? – Since our original number is less than one, it has to stay less than one, so which way do we go? To the left!

n 1. 5 n x 10 -1 = 0. 0015 x 102 Note that we moved in the positive direction to change the exponent from -1 to 2, and the negative direction to change the decimal.
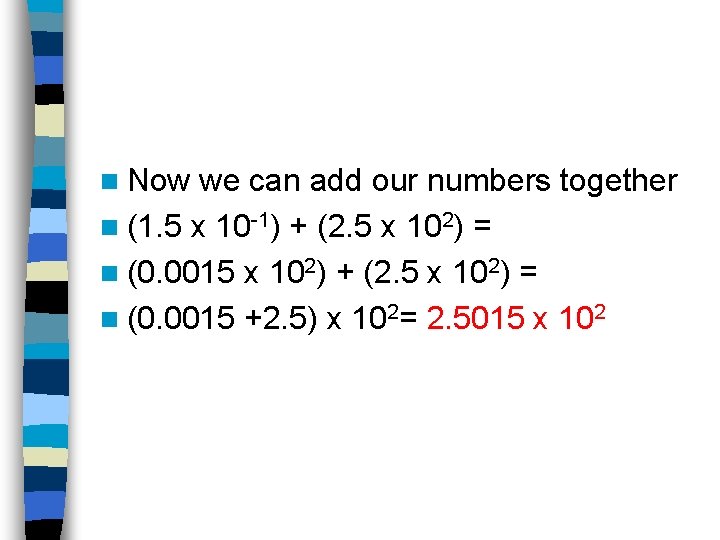
n Now we can add our numbers together n (1. 5 x 10 -1) + (2. 5 x 102) = n (0. 0015 x 102) + (2. 5 x 102) = n (0. 0015 +2. 5) x 102= 2. 5015 x 102

Let’s try to make both exponents -1… n (1. 5 x 10 -1) + (2. 5 x 102) = n 2. 5 x 102 =____ x 10 -1 n To get from 102 to 10 -1, we must move three places in the negative direction. n So we will move our decimal 3 places in the positive direction n 2. 5 x 102 =2500 x 10 -1

n Now we can add our numbers n (1. 5 x 10 -1) + (2500 x 10 -1) = n (1. 5 + 2500) x 10 -1= 2501. 5 x 10 -1

n Note that our answer is not in correct form (one nonzero digit to left of decimal) so we need to put it in correct form: use the same logic n Move decimal three places in negative direction, then move exponent three places in positive direction n 2501. 5 x 10 -1 = 2. 5015 x 102

So, to change an exponent… n If you are going in the positive direction to get to the new exponent, move the decimal in the negative direction. n If you are going in the negative direction to get to the new exponent, move the decimal in the positive direction.

A note about scientific notation and your calculator… n On the graphing calculator, scientific notation is best done with the button. 4. 58 x 106 is typed 4. 58 6 n The other option is to use the 4. 58 x 10 6 But you have to be careful with this when dividing and make sure you use parantheses!

Use a calculator to evaluate: -5 4. 5 x 10 1. 6 x 10 -2 n Type 4. 5 -5 1. 6 n You -2 must include parentheses if you don’t use the !! key but 10 instead! n (4. 5 x 10 -5) (1. 6 x 10 -2) n =0. 0028125 n Write in scientific notation. n =2. 8125 x 10 -3

n DON’T FORGET!!! n When you are copying an answer from your calculator screen make sure you include the scientific notation if present. n If your calculator answer was 1. 93 E-2 you would copy down 1. 93 x 10 -2 on your paper. The “E” in the answer means “x 10”