Scientific Notation Scientific notation was developed to allow

Scientific Notation • Scientific notation was developed to allow you to easily represent extremely large, or extremely small numbers. • The number of zeroes makes a huge difference! • Makes it much easier to add, multiply, and divide large numbers.

Scientific Notation • The little number to the upper right of the ten is called an exponent. • 1011 • The exponent is also known in scientific notation as the “power of ten” as it is how many times the number is multiplied by ten!

Scientific Notation • The Andromeda Galaxy has at least 200, 000, 000 stars in it. • This could be seen as: 2 X 100, 000, 000. • 100, 000, 000 seems like a huge number, but it is just 10 times itself…. 11 times. • (10 x 10 x 10 x 10) = 100, 000, 000! • So therefore 100, 000, 000 = 1011

Scientific Notation • The positive exponent refers to how many zeroes follows the 1…. • 100 = 1 • 101 = 10 • 102 = 100 • 103 = 1, 000 • Etc….

Scientific Notation • With a negative exponent, we see the same thing, the number of zeroes after 1…. But this time, 1 is being divided by that number. • 10 -1 = 1/10 =. 1 • 10 -2 =1/100 =. 01 • 10 -3 =1/1, 000 =. 001 • 10 -4 =1/10, 000 =. 0001 • Etc….

Scientific Notation • So… if we have 200, 000, 000 it can be represented as… • 2. 0 X 1011 • This is read as “Two point zero times ten to the eleventh. ”

Scientific Notation • Let’s try this with a few other numbers… • 2. 5 X 103 = 2500 • 2. 5 X 10 -3 =. 0025 • 9 X 106 = 9, 000 • 4 X 10 -5 =. 00004

Scientific Notation • Now try it on your own! • 3 X 103 = • 7 X 10 -4 = • 3. 5 X 10 -2 = • 3. 5 X 102 = • 7. 6 X 107 = • 2. 2 X 10 -6 =

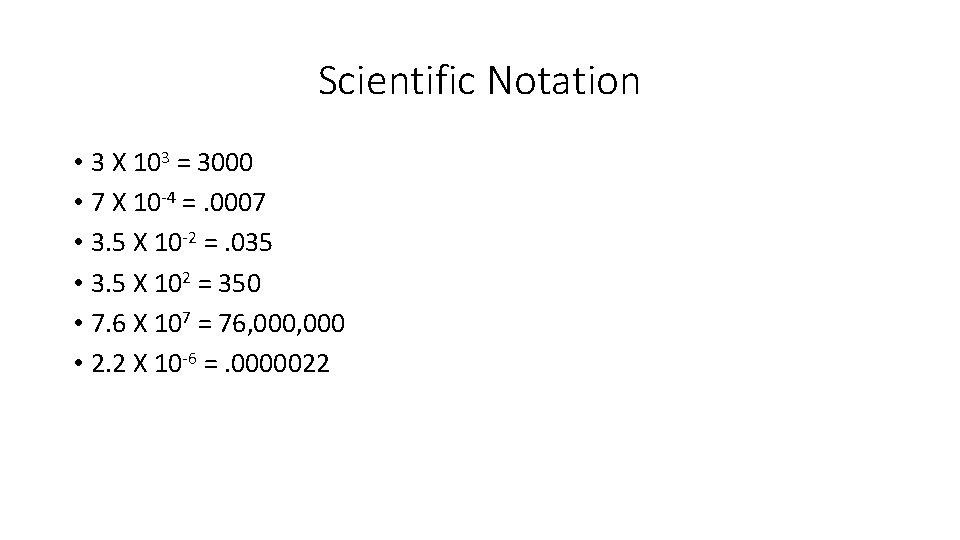
Scientific Notation • 3 X 103 = 3000 • 7 X 10 -4 =. 0007 • 3. 5 X 10 -2 =. 035 • 3. 5 X 102 = 350 • 7. 6 X 107 = 76, 000 • 2. 2 X 10 -6 =. 0000022

Scientific Notation • Sometimes, in exchange for the 10 we use an “E” instead. • The “E” stands for exponent. • So… 5 X 104 can sometimes be expressed as… 5 E 4. • 5 E 4 Just means 5. 0 X 10 and raised to the 4 th power. • 5 E 4 = 50, 000 • 5 X 104 = 50, 000

Scientific Notation • But wait, wasn’t this supposed to make adding, subtracting, dividing and multiplying easier between huge or small numbers? • Yes! Yes it does!

Scientific Notation • So now we are going to add and subtract some big numbers in an easy way! The key is in keeping the exponents the same! • First, change the exponent of 2 to 3, and make the 2 the right value to reflect that change. • (2. 0 X 102) + (3. 0 X 103) = (. 2 X 103) + (3. 0 X 103) • Now add the two numbers in front… • . 2 + 3. 0 = 3. 2 • And keep the exponent. . . • 3. 2 X 103 = 3, 200 • And now you have your answer! Lets double check our math.

Scientific Notation • Now let’s try subtraction! Again, the key is to make the exponents the same. • (2. 0 X 107) – (6. 3 X 105) = (200 X 105) – (6. 3 X 105) • = 193. 7 X 105 • Which rewritten is… 1. 937 X 107 • So lets double check that… • 20, 000 – 630, 000 = 19, 370, 000 = 1. 937 X 107 • Is it getting easier?

Scientific Notation • Multiplying very large numbers or very small numbers becomes much easier using Scientific Notation. The reason being is that every thing goes by orders of 10. • 101 X 102 = 10 X 100 = 1, 000 = 103 • You are adding the exponents! • 101+2 = 103

Scientific Notation • You multiply the numbers in front, and add the exponents together! • (4. 0 X 105) X (3. 0 X 10 -1) = • The 4 and 3 are multiplied, 4 X 3, making 12. • The exponents are added, 5 -1, and make 4. • So the answer is: 12 X 104 • But… This isn’t in the correct form… So let’s fix that! • 1. 2 X 105 • Not too bad!

Scientific Notation • Lets try a problem on our own now… • (5. 5 X 104) X (4. 0 X 105) =

Scientific Notation • Answer • (5. 5 X 104) X (4. 0 X 105) = 22 X 109 = 2. 2 X 1010