SCIENTIFIC NOTATION Scientific notation is a way of

SCIENTIFIC NOTATION

Scientific notation �is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. �In scientific notation all numbers are written in the form of �a is the number between 1 and 10 , b the exponent is a positive or negative integer.

Example • An electron's mass is about 0. 00000000000000091093822 kg. In scientific notation, this is written 9. 1093822× 10− 31 kg. • The Earth's mass is about 597360000000000 kg. In scientific notation, this is written 5. 9736× 1024 kg. • The Earth's circumference is approximately 40000000 m. In scientific notation, this is 4× 107 m • Explanation: � count the number of the places that the decimal point must be moved to give the number a. If the decimal point has to be moved to the left then b is positive integer ; if it has to be moved to the right, b is negative integer. 568. 762 = 5. 68762 x 10 2 0. 00000772 = 7. 72 X 10 -6

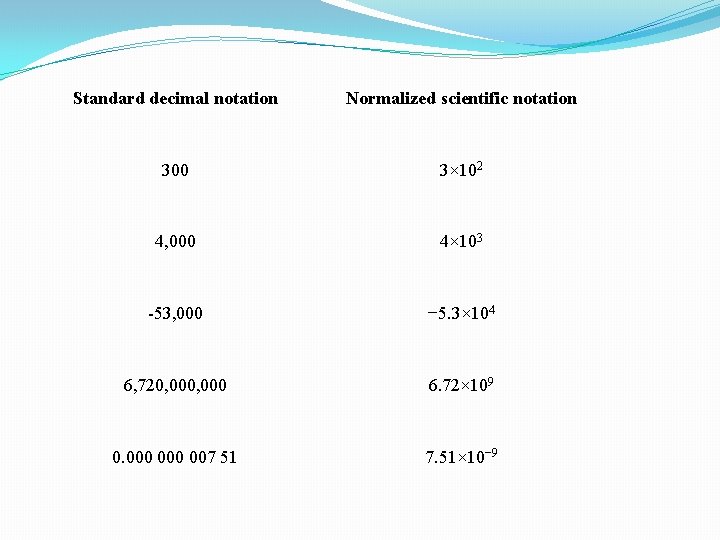
Standard decimal notation Normalized scientific notation 300 3× 102 4, 000 4× 103 -53, 000 − 5. 3× 104 6, 720, 000 6. 72× 109 0. 000 007 51 7. 51× 10− 9

Addition and Subtraction 1 - write each quantity – a 1 and a 2 with the same exponent b. 2 - combine a 1 and a 2 ; the exponents remain the same ( 4. 31 X 104 ) + ( 3. 9 X 103 ) = ( 4. 31 X 104 ) + ( 0. 39 X 104) = 4. 70 X 104 ( 2. 22 X 10 -2 ) - ( 4. 1 X 10 -3 ) = ( 2. 22 X 10 -2 ) - ( 0. 41 X 10 -2) = 1. 81 X 10 -2

Multiplication and Division 1 - multiply a 1 and a 2 , but add the exponents together. 2 - divide a 1 and a 2 , and subtract the exponents. ( 8. 0 X 104 ) X ( 5. 0 X 102 ) = ( 8. 0 X 5. 0 ) (104+2) = 40 X 106 = 4. 0 X 107 ( 4. 0 X 10 -5 ) X ( 7. 0 X 103 ) = ( 4. 0 X 7. 0 ) (10 -5+3) = 28 X 10 -2 = 2. 8 X 10 -1 ( 6. 9 X 107 ) / ( 3. 0 X 10 -5 ) = ( 6. 9 / 3. 0 ) 107 -(-5) = 2. 3 X 1012