Scientific Notation Conversions and Significant Digits Learning Goals

Scientific Notation, Conversions and Significant Digits Learning Goals … … convert numbers to scientific notation … convert measurements using the metric system … identify the number of significant digits in a measurement

Scientific Notation Ex) Convert the following to scientific notation: 5. 3 x 10 -5 (a) 0. 000053 = ___________ (b) 7 4. 0 x 10 40 000 = __________ (c) 1. 33 x 10 -5 (2. 63 x 10 -9)(5. 06 x 103) = _______ • Note: use the exponent button on your calculator EXP, E, EE Try working on Practice Questions …

Practice Questions: 1. Express the following numbers in scientific notation: a) 100300000 = _____________ 1. 003 x 1012 3. 998 x 10 -10 b) 0. 000003998 = _____________ 5. 823 x 101 c) 58. 23 = _____________ 2. 038 x 10 -1 d) 0. 2038 = _____________ 1. 2452 x 104 e) 12452 = _____________ 2. Express the following numbers to decimal notation: 17700000 a) 1. 77 x 107 = ____________ 0. 00002552 b) 2. 552 x 10 -9 = _____________ 1180 c) 1. 18 x 103 = _____________ 0. 444 d) 4. 44 x 10 -1 = _____________ e) 1. 399 x 100 = _____________ 1. 399 3. Express the results of the following operations in scientific notation: 1. 42 x 10 -2 a) 1. 39 x 10 -2 + 3. 11 x 10 -4 = _____________ b) 1. 17 x 104 - 3. 57 x 102 = _____________ 1. 13 x 104 1. 92 x 1017 c) (1. 81 x 10 -3) (1. 06 x 1020) = _____________ d) (5. 77 x 10 -4) (1. 71 x 10 -11) = _____________ 3. 37 x 107

Volume • Cubic units (m 3, cm 3, mm 3) Vs. Capacity units (m. L, L, k. L) • Cubic units can be converted to capacity units (and vice versa) using the following conversions: 1 cm 3 = 1 m. L 1000 cm 3 = 1000 m. L = 1 L 1 m 3 = 1000 L 1 m 3 = (100 cm)(100 cm) 1 m 3 = 1000000 cm 3 = 1000000 m. L 1 m 3 = 1000 L

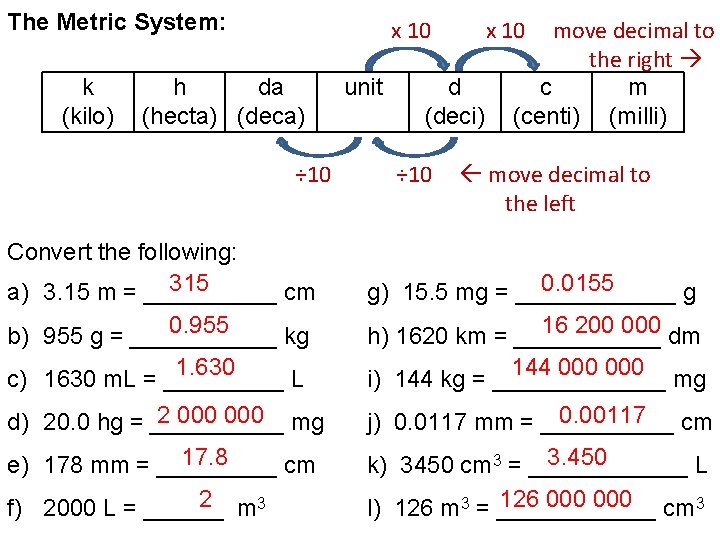
The Metric System: k (kilo) x 10 h da (hecta) (deca) ÷ 10 Convert the following: 315 a) 3. 15 m = _____ cm 0. 955 b) 955 g = ______ kg 1. 630 c) 1630 m. L = _____ L 2 000 mg d) 20. 0 hg = _____ 17. 8 e) 178 mm = _____ cm 2 m 3 f) 2000 L = ______ unit x 10 d (deci) ÷ 10 move decimal to the right c m (centi) (milli) move decimal to the left 0. 0155 g) 15. 5 mg = ______ g 16 200 000 dm h) 1620 km = ______ 144 000 mg i) 144 kg = _______ 0. 00117 cm j) 0. 0117 mm = _____ 3. 450 k) 3450 cm 3 = ______ L 126 000 cm 3 l) 126 m 3 = ______

Significant Digits • Non-zero digits are always significant. 2 (eg) 22 ______ significant digits 3 22. 3 ______ significant digits • With zeros, the situation is more complicated: 1. Zeros placed before other digits are not significant (place holders) 2 (eg) 0. 046 ______ significant digits 4 (eg) 0. 005487 g ______ significant digits 2. Zeros placed between other digits are always significant. 4 (eg) 20. 64 L ______ significant digits 4 (eg) 4009 kg ______ significant digits

3. Zeros that exist after the decimal place to demonstrate accuracy are significant. (eg) 46. 20 4 ______ significant digits (eg) 3. 000 4 ______ significant digits 4. Zeros that exist at the end of a number are significant only if they are behind a decimal point. If the zeros at the end of a number do not follow a decimal point, they are not significant (place holders) (eg) 382 000 3 ______ significant digits (eg) 382 000. 0 7 ______ significant digits

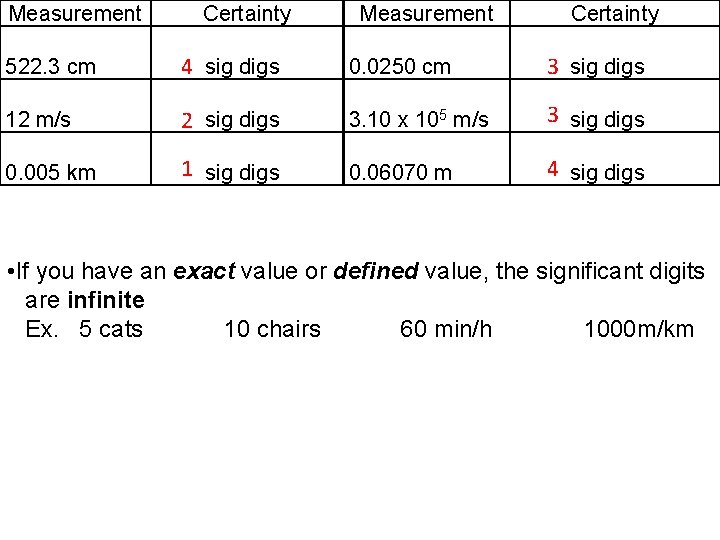
Measurement Certainty 522. 3 cm 4 sig digs 0. 0250 cm 3 sig digs 12 m/s 2 sig digs 3. 10 x 105 m/s 3 sig digs 0. 005 km 1 sig digs 0. 06070 m 4 sig digs • If you have an exact value or defined value, the significant digits are infinite Ex. 5 cats 10 chairs 60 min/h 1000 m/km

ROUNDING • If the digit after the digit to be retained as significant is a greater than 5, round up • If the digit after the digit to be retained as significant is a 4 or less, round down • If the digit after the digit to be retained as significant is exactly 5: • if the digit to be retained is odd, round up • if the digit to be retained is even, round down Round the following to a whole number: 92 79 a) 91. 8 _______ d) 78. 58 _______ 52 b) 52. 3 _______ e) 42. 5 _______ 42 38 38 c) 37. 53 _______ f) 37. 5 _______

CALCULATIONS INVOLVING SIGNIFICANT DIGITS ADDITION AND SUBTRATION • Precision Rule – Precision is defined as the place value of the last digit obtained from a measurement or calculation • When adding or subtracting, the final answer has the same number of decimal places as the number with the least number of decimal places. 1 The least number of decimal places is ____ (eg) 26. 1 6. 6 m + 18. 74 m + 0. 766 m = _________

Multiplication and Division • When multiplying or dividing, the final answer must have the same number of significant figures as the original number with the fewest significant figures (we can’t be any more certain than we were to begin with) (eg) Calculate the volume of a box with sides measuring 5. 05 cm, 3. 87 cm and 4. 7 cm V = (5. 05 cm x 3. 87 cm x 4. 7 cm) = 91. 85445 cm 3 = 92 cm 3

CAN I … … convert numbers to scientific notation … convert measurements using the metric system … identify the number of significant digits in a measurement HOMEWORK WS “Significant Digits” Complete any Practice Questions