Scientific Methods 1 Scientific evaluation experimental design statistical

Scientific Methods 1 ‘Scientific evaluation, experimental design & statistical methods’ COMP 80131 Lecture 6: Statistical Methods-Significance Barry & Goran www. cs. man. ac. uk/~barry/mydocs/my. COMP 80131 22 Nov 2011 COMP 80131 -SEEDSM 6 1

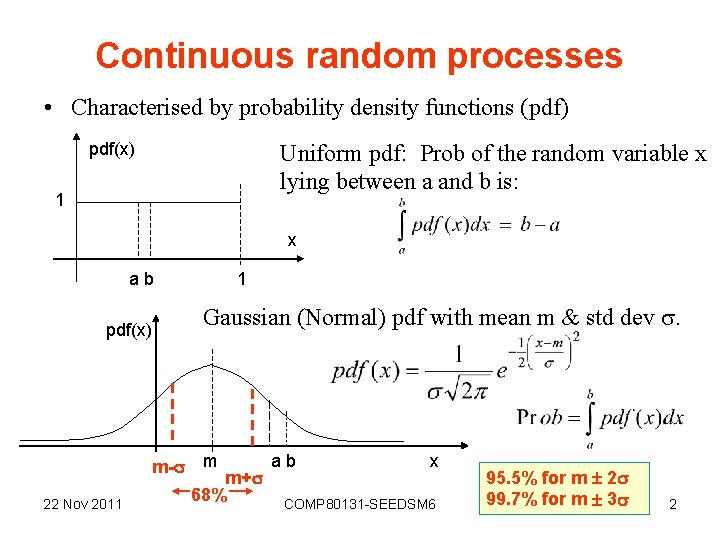
Continuous random processes • Characterised by probability density functions (pdf) pdf(x) Uniform pdf: Prob of the random variable x lying between a and b is: 1 x ab pdf(x) m- 22 Nov 2011 1 Gaussian (Normal) pdf with mean m & std dev . m m+ 68% ab x COMP 80131 -SEEDSM 6 95. 5% for m 2 99. 7% for m 3 2

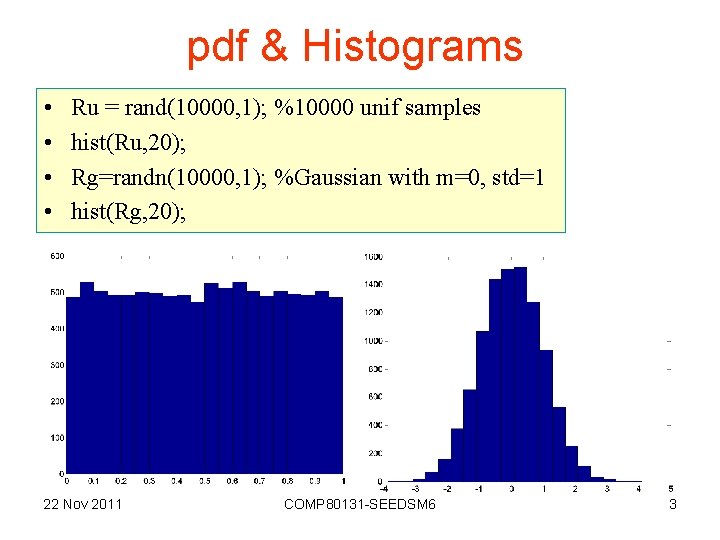
pdf & Histograms • • Ru = rand(10000, 1); %10000 unif samples hist(Ru, 20); Rg=randn(10000, 1); %Gaussian with m=0, std=1 hist(Rg, 20); 22 Nov 2011 COMP 80131 -SEEDSM 6 3

Convert histogram to estimate of pdf • Divide each column by number of samples • Then multiply by number width of bins. • For better approximation, increase number of bins 22 Nov 2011 COMP 80131 -SEEDSM 6 4

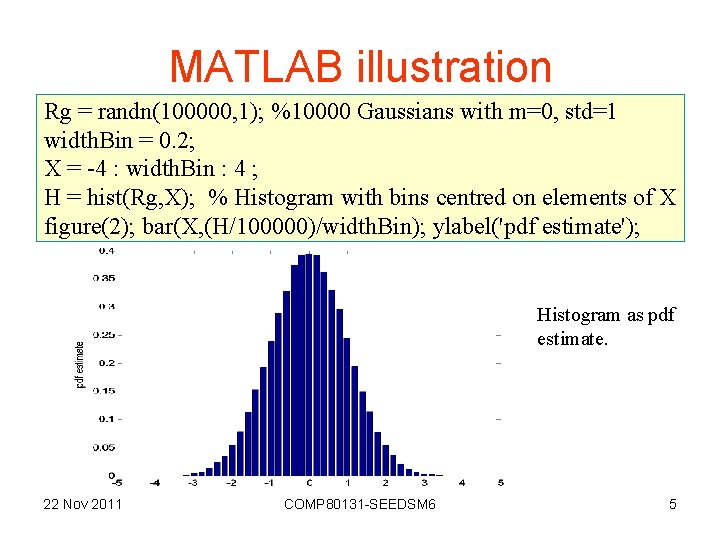
MATLAB illustration Rg = randn(100000, 1); %10000 Gaussians with m=0, std=1 width. Bin = 0. 2; X = -4 : width. Bin : 4 ; H = hist(Rg, X); % Histogram with bins centred on elements of X figure(2); bar(X, (H/100000)/width. Bin); ylabel('pdf estimate'); Histogram as pdf estimate. 22 Nov 2011 COMP 80131 -SEEDSM 6 5

Gaussian (normal) pdf • Measurements {xi} of many naturally occurring phenomena tend to be normally distributed with some mean m & std . • Let zi = (xi - m)/ , • Then {zi} will have a standard normal pdf with mean = 0 & std = 1. 22 Nov 2011 COMP 80131 -SEEDSM 6 6

Plot true standard normal pdf Mean=0; Std=1; K = 1/( Std*sqrt(2*pi) ); X = -4*Std : width. Bin : 4*Std ; for I=1: length(X); G(I) = K * exp(-(X(I)-Mean)^2 / (2*Std^2) ); end; figure(4); plot(X, G); ylabel('pdf'); Gaussian pdf 0. 4 0. 35 0. 3 0. 25 0. 2 0. 15 0. 1 0. 05 22 Nov 2011 0 -4 -3 -2 -1 0 1 2 x COMP 80131 -SEEDSM 6 3 4 7

Plot Gaussian cdf X=-4: 0. 1: 4; C = normcdf(X, 0, 1); figure(1); plot(X, C); grid on; xlabel('x'); ylabel('prob that var < x'); Cumulative density function (cdf) Probability of Gaussian variable (m=0 std=1) being < x. No formula for this. Use MATLAB function: normcdf(X, m, std) 22 Nov 2011 COMP 80131 -SEEDSM 6 8

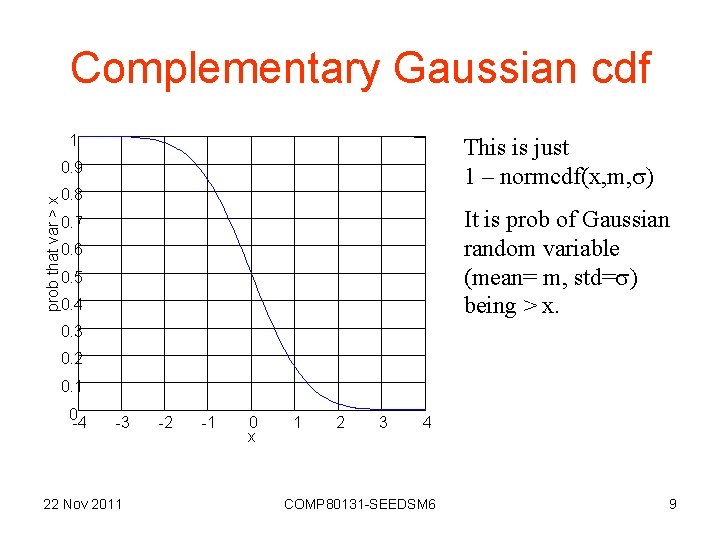
Complementary Gaussian cdf 1 This is just 1 – normcdf(x, m, ) 0. 9 prob that var > x 0. 8 It is prob of Gaussian random variable (mean= m, std= ) being > x. 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0 -4 -3 22 Nov 2011 -2 -1 0 x 1 2 3 4 COMP 80131 -SEEDSM 6 9

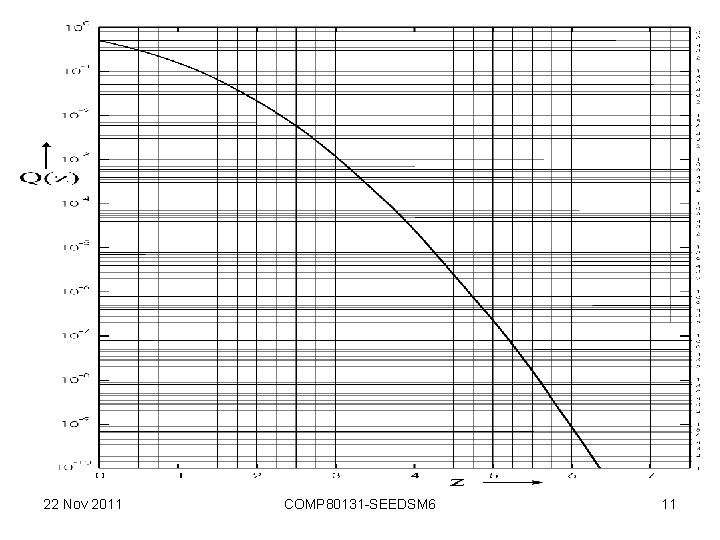
Complementary error function • Some call the complementary Gaussian cdf (m=0, =1) the ‘complementary error function’ Q(z) • But ‘erfc’ is also called this. • Q(z) = comp-Gaussian cdf= 0. 5 erfc(-z/ 2). • Used to rely on tables & graphs of Q(z). • When m 0 & 1, use Q((z-m)/ ) 22 Nov 2011 COMP 80131 -SEEDSM 6 10

22 Nov 2011 COMP 80131 -SEEDSM 6 11

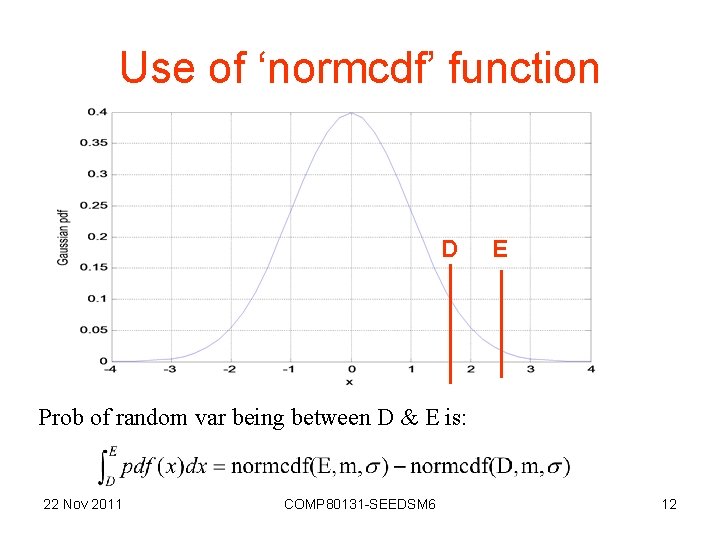
Use of ‘normcdf’ function D E Prob of random var being between D & E is: 22 Nov 2011 COMP 80131 -SEEDSM 6 12

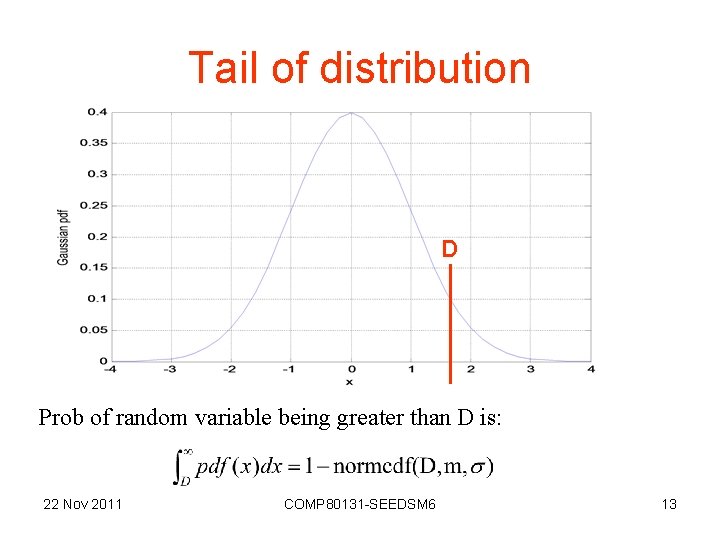
Tail of distribution D Prob of random variable being greater than D is: 22 Nov 2011 COMP 80131 -SEEDSM 6 13

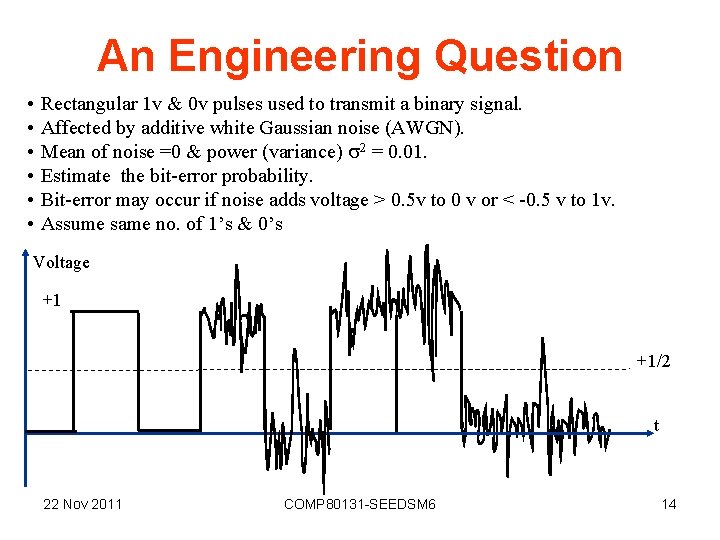
An Engineering Question • • • Rectangular 1 v & 0 v pulses used to transmit a binary signal. Affected by additive white Gaussian noise (AWGN). Mean of noise =0 & power (variance) 2 = 0. 01. Estimate the bit-error probability. Bit-error may occur if noise adds voltage > 0. 5 v to 0 v or < -0. 5 v to 1 v. Assume same no. of 1’s & 0’s Voltage +1 +1/2 t 22 Nov 2011 COMP 80131 -SEEDSM 6 14

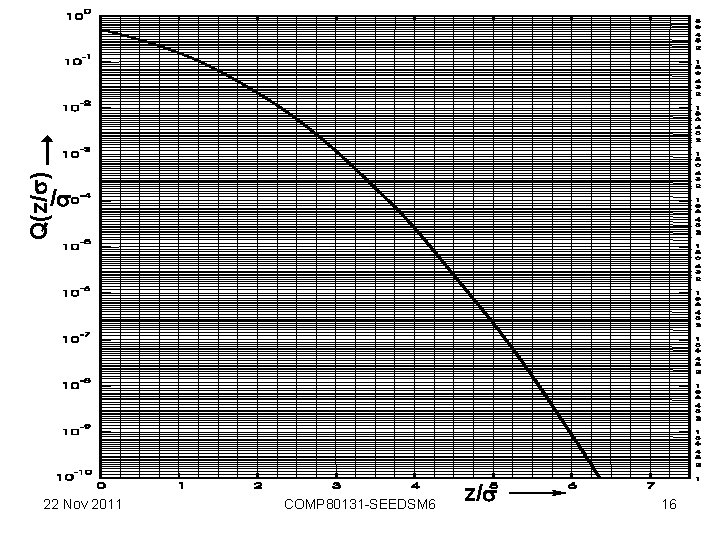
Solution prob(error) = prob(noise > 0. 5) when bit =0 + prob(noise < -0. 5) when bit =1 = 0. 5 prob(noise > 0. 5) +0. 5 prob(noise < -0. 5) = prob(noise > 0. 5) because of symmetry = 1 - normcdf(0. 5, 0, 0. 1) = 2. 9 10 -7 Or, using graph Q(z/ ) on next page, prob(error) = Q(0. 5/0. 1) = Q(5) 3 10 -7 22 Nov 2011 COMP 80131 -SEEDSM 6 15

Q(z/ ) / 22 Nov 2011 COMP 80131 -SEEDSM 6 z/ 16

Back to sampling A population has true mean & std . Take a sample of N measurements from it – say N=50 Calculate sample-mean m 1 & std s 1. If population is Gaussian, pdf of m 1 will be Gaussian with mean = & std = s 1 = / N. • Can confirm by taking more samples to obtain sample-means & stds: m 1, m 2, …, m. M & s 1, s 2, …, s. M • Estimate mean & std of sample-means • Also mean & std of sample-variances (later) • • 22 Nov 2011 COMP 80131 -SEEDSM 6 17

Significance testing • • • Assume pop-mean (‘mu’)may change with pop-std fixed at . Assume know pop-std & that it will not change. We can only take one sample of 50 values. Calculate m 1 to decide whether pop-mean has changed. Null Hypothesis – it has not changed. new pop-mean New = • If Null Hyp is true, pdf of sample-mean is on next slide: 22 Nov 2011 COMP 80131 -SEEDSM 6 18

Concept of a ‘null-hypothesis’ • A null-hypothesis is an assumption that is made and then tested by a set of experiments designed to reveal that it is likely to be false, if it is false. • Testing is done by considering how probable the results are, assuming the null hypothesis is true. • If the results appear very improbable the researcher may conclude that the null-hypothesis is likely to be false. • This is usually the outcome the researcher hopes for when he or she is trying to prove that a new technique is likely to have some value. 22 Nov 2011 COMP 80131 -SEEDSM 6 19

Gaussian pdf of sample-mean m 1 0. 4 0. 35 0. 3 0. 25 0. 2 0. 15 0. 1 0. 05 0 s 1 = / 50 -2 s 1 -s 1 +2 m 1 +4 s 1 Assume value we got was m 1 = + 2. 5 s 1. How unlikely if Null Hyp is true? 22 Nov 2011 COMP 80131 -SEEDSM 6 20

p-value • “Probability of obtaining a test result at least as extreme as the one that was actually observed, assuming that the null hypothesis is true”. • Reject the null hypothesis if the p-value is less than some value α (significance level) which is often 0. 05 or 0. 01. • When the null-hypothesis is rejected, the result is said to be statistically significant. • Here p-value is 1 - normcdf(m 1, , s 1) …with s 1= / N • = 1 -normcdf( +2. 5 s 1, , s 1) • = 1 - normcdf(2. 5 , 0, 1) = 0. 0062 • Much less than 0. 01 so reject NH at 1% confidence level. • Conclude that mean has changed. 22 Nov 2011 COMP 80131 -SEEDSM 6 21

Our 2 assumptions • That was easy because we made 2 assumptions: population is Gaussian & pop-std is known to us. • Now need to eliminate these 2 assumptions. • We have some help from the Central Limit Theorem: 22 Nov 2011 COMP 80131 -SEEDSM 6 22

Central Limit Theorem • If samples of size N are ‘randomly’ chosen from a pop with mean & std , the pdf of their mean, m 1 say, approaches a Normal (Gaussian) pdf with mean & std / N as N is made larger & larger. • Regardless of whether the population is Gaussian or not! • Previous example can be made to work for non-Gaussian pop provided N is ‘large enough’. • More on this next week. 22 Nov 2011 COMP 80131 -SEEDSM 6 23

Another example • Assume we wish to find out if a proposed technique designed to benefit users of a system is likely to have any value. • Divide the users into two groups and offer the proposed technique to one group and something different to the other group. • The null-hypothesis would be that the proposed technique offers no measurable advantage over the other techniques. 22 Nov 2011 COMP 80131 -SEEDSM 6 24

The testing • This would be carried out by looking for differences between the sets of results obtained for each of the two groups. • Careful experimental design will try to eliminate differences not caused by the techniques being compared. • Must take a large number of users in each group & randomize the way the users are assigned to groups. • Once other differences have been eliminated as far as possible, any remaining difference will hopefully be indicative of the effectiveness of the techniques being investigated. • The vital question is whether they are likely to be due to the advantages of the new technique, or the inevitable random variations that arise from the other factors. • Are the differences statistically significant? • Can employ a statistical significance to find out. 22 Nov 2011 COMP 80131 -SEEDSM 6 25

Failure of the experiment • If the results are not found to look improbable under the nullhypothesis, i. e. if the differences between the two groups are not statistically significant, then no conclusion can be made. • The null-hypothesis could be true, or it could still be false. • It would be a mistake to conclude that the ‘null-hypothesis’ has been proved likely to be true in this circumstance. • It is quite possible that the results of the experiment give insufficient evidence to make any conclusions at all. 22 Nov 2011 COMP 80131 -SEEDSM 6 26

Question: fair coin test Checking whether a coin is fair Suppose we obtain heads 14 times out of 20 flips. The p-value for this test result would be the probability of a fair coin landing on heads at least 14 times out of 20 flips. From binomial distribution formula( Lecture 4), this is: (20 C 14 + 20 C 15+20 C 16+20 C 17+20 C 18+20 C 19+20 C 20) / 220 = 0. 058 This is probability that a fair coin would give a result as extreme or more extreme than 14 heads out of 20. 22 Nov 2011 COMP 80131 -SEEDSM 6 27

Significance test for fair coin question • Reject null-hypothesis if p-value α. • If α= 0. 05, rejection of null-hypothesis is: “at the 5% (significance) level”. • Probability of wrongly rejecting null-hypothesis (Type 1 error) will be equal to α. • This is considered sufficiently low. • In this case, p-value > 0. 05, therefore observation is consistent with null-hypothesis & we cannot reject it. • Cannot conclude that coin is likely to be unfair. • But we have NOT proved that coin is likely to be fair. • 14 heads out of 20 flips can be ascribed to chance alone • It falls within the range of what could happen 95% of the time with a fair coin. 22 Nov 2011 COMP 80131 -SEEDSM 6 28

Questions from Lecture 2 • Analyse the ficticious exam results & comment on features. • Compute means, stds & vars for each subject & histograms for the distributions. • Make observations about performance in each subject & overall • Do marks support the hypothesis that people good at Music are also good at Maths? • Do they support the hypothesis that people good at English are also good at French? • Do they support the hypothesis that people good at Art are also good at Maths? • If you have access to only 50 rows of this data, investigate the same hypotheses • What conclusions could you draw, and with what degree of certainty? 22 Nov 2011 COMP 80131 -SEEDSM 6 29

Questions from L 4 1. 2. A patent goes to a doctor with a bad cough & a fever. The doctor needs to decide whether he has ‘swine flu’. Let statement S = ‘has bad cough and fever’ & statement F = ‘has swine flu’. The doctor consults his medical books and finds that about 40% of patients with swine-flu have these same symptoms. Assuming that, currently, about 1% of the population is suffering from swine-flu and that currently about 5% have bad cough and fever (due to many possible causes including swine-flu), we can apply Bayes theorem to estimate the probability of this particular patient having swine-flu. A doctor in another country knows form his text-books that for 40% of patients with swine-flu, the statement S, ‘has bad cough and fever’ is true. He sees many patients and comes to believe that the probability that a patient with ‘bad cough and fever’ actually has swine-flu is about 0. 1 or 10%. If there were reason to believe that, currently, about 1% of the population have a bad cough and fever, what percentage of the population is likely to be suffering from swine-flu? 22 Nov 2011 COMP 80131 -SEEDSM 6 30